隐函数求导方法：
方法一：
将y看成关于x的函数，即 (1/y)'=y'/2y
方法二：
eg: xy + lnx + lny = 0; 令F(x,y) = xy + lnx+ lny
隐函数存在定理1： dy /dx = - Fx/Fy,
其条件：1.具有连续偏导数； 2.F(x0,y0) =0，即存在零点； 3.Fy(x0,y0)=/=0,即隐函数的偏导不为零
二元隐函数微分法：
隐函数存在定理2：
，
注意，求偏导时，相互独立，互不影响。
解方程组时，可以运用行列式求解。
雅可比行列式(隐函数存在定理3)：
假设有： F=f(u,v), u= f(x,y) , v = f(x,y) 以及 G = f(u,v), u = f(x,y) ,v = f(x,y)
雅可比行列式（系数行列式）：
，记作 J = 
则有: 
,
,注意，它们不是对称关系！！！
方向导数：
前提： 1.可微 ； 2.二元函数及以上；
记法： 
计算法则：
推广：（三元）
其中，cosα，cosβ，cosγ 称为： 方向余弦； cosα = x/ |
|
eg: 求 u = x^2*y*z 在点p(1,1,1) 沿方向(2,-1,3) 的方向导数
梯度：
grad f(x,y) = (fx,fy)向量；
方向导数是一个数，梯度，是一个向量；
方向导数 = 梯度 与 方向L的单位向量 的数量积；
= 梯度 的模长 * 1 * cos <梯度，方向L>
多元函数的极值及求法：
多元函数的极值的必要条件：
fx(x0,y0)=0, fy(x0,y0) =0,即 有驻点
注意: 极值点 --->驻点 驻点 --/->极值点
多元函数有极值的充分条件：
函数具有一阶以及二阶 连续偏导,令fxx(x0,y0) = A ,fyy(x0,y0)=C,令 fxy(x0,y0) = B
1.当 AC-B^2 >0时，有极值，若 A<0,为极大值，若A>0,为极小值
2.当AC-B^2 < 0时，无极值；
3.当AC-B^2 = 0时，可能有极值，也可能没有极值；（注意，若二阶偏导含有xy，将驻点值代入即可）
极值点可能是驻点，也可能是不可导点（常见的比如: 分母为零等限制）；
最值可能在极值点，也可能在定义域边界上存在。
二元函数的最值同理； 要么将驻点值代入比对； 要么将定义域边界代入比对；
条件极值：
拉格朗日乘数法：
1.构造一个新函数 L(x,y) = f(x,y) + λφ(x,y)， 其中，λ称为拉格朗日乘子； φ(x,y)称为条件函数； f(x,y)称为目标函数
2.求驻点；
3.构造方程组： 各自的偏导=0,以及 φ(x)=0;
eg: u = xyz, φ(x)=1/x+ 1/y + 1/z - 1/a;
构造方程组： 
，
思路： 对程序； ---> 求 xyz----> 回代 ---> 求x,y,z;
二重积分：
物理意义：
曲顶柱体的体积： V = 
，其中， λ=1/n
记作： 
其中, D叫做积分区域；
dσ叫做 面积元素；
f(x,y)叫做 被积函数；
x,y叫做 积分变量；
性质：
1.线性性： 即 满足数乘分配律；
2.积分区域的可加性
3.若 f(x,y) = 1 , 则 
4.保不等式性： 若 f(x,y) <= g(x,y) ,则有：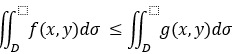 
另： 
5.积分估值： 若 f 在区域D中，有m<= f(x,y) <= M， 则有：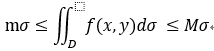 
6.二重积分中值定理：
注：定积分的中值定理： 
二重积分的计算：
1.利用直交坐标计算D的面积： 分为x型面积； y型面积；
其中，x型面积： 
y型面积： 
x型面积时，y的上下界只能用线段表示，而不能用点表示；
同理，y型面积时，x的上下界只能用线段方程表示，而不能用点 表示；
通常在计算时，可以将xy分开，因为针对特定的积分变量，其余变量都视作常数。
eg: 
在选取x型与 y 型区域时候，利用好技巧则会简化很多：
eg: 
, D是直线y=x,y=0,x=π,所围成的闭区域； （看成什么型，就对什么后积分）
若先对y积分，再对x积分就很简单； （这是一个偶然性，但是从出题者角度来说则是必然性。）
若先对x积分，再对y积分就很复杂；
交换积分顺序的技巧：
1.画出积分区域D；
2.将要转换的顺序按照 直角坐标系 法则进行转换
eg: I = 
2.利用极坐标系计算二重积分：
公式： 
注意，在极坐标系中，只有θ型区域；
当，f(r*cosθ, r*sinθ) = 1时，有： 
eg: 计算： 
注意，直交坐标系与 极坐标系的转化 需要靠 D的区域作为桥梁；一般情况下，圆形等特殊图形才可进行转化；
鉴于θ极坐标系中，只有θ型，而此时 ,r 的范围： 注意，本质上仍是用关于θ的表达式表示，但是大多数情况下其表现出来的则是两个单独的点。 （这是由于圆锥曲线的特殊性等决定的。）
3.二重积分换元法（用于辅助）：
其中： J(u,v) 为雅可比行列式: J(u,v) = 
，此时x,y充当的中间函数，u,v充当的最终变量
前提： 1.x(u,v),y(u,v) 在D' 上具有一阶 连续偏导数
2.J(u,v) =/=0
3.变换 D' -> D 是 一对一的；
计算原则与步骤：
1.画出积分域；
2.选择坐标系；
3.确定积分序；
4.写出积分限（根据图示法， 或者 不等式）
5.计算要简便（充分利用对称性，充分利用图形（即选取坐标系，选取区域形状方面））