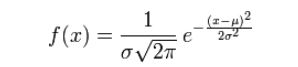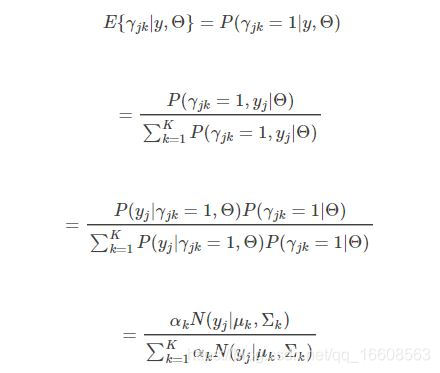高斯混合模型(GMM Gaussian Mixture Model)

高斯混合模型是一种业界广泛使用的聚类算法，该方法使用了高斯分布作为参数模型，并使用了期望最大算法（EM）进行训练。

什么是高斯分布

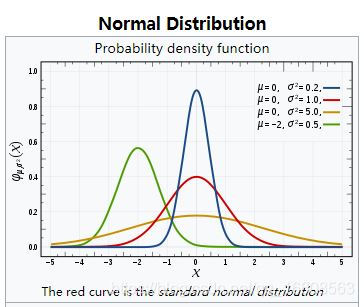
高斯分布有时也被称作正态分布，是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面都有着重大的影响。

若随机变量X服从一个数学期望为 $μ$、标准方差为 $σ^2$的高斯分布，记作：
$X~N(μ,σ^2)$
则其概率密度函数为：


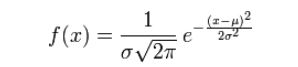
公式中含有2个参数，参数 $μ$表示均值，参数 $σ$表示标准差，均值决定了其位置，标准差决定了分布的幅度。

有了概率密度函数，在已知参数 $μ，σ$的前提下，输入变量x，可以获得其相对应的概率密度。

高斯混合模型

定义：高斯混合模型是指具有如下形式的概率分布模型：
$P(y|θ)=\displaystyle\sum_{k=1}^{K}α_kφ(y|θ_k)$ (1)

其中， $α_k$是系数，且 $α_k≥0，\displaystyle\sum_{k=1}^{K}α_k=1$; $φ(y|θ_k)$是高斯分布密度函数，其中 $θ_k=(μ_k，σ_k)$

$φ(y|θ_k)=\frac{1}{\sqrt{2π}σ_k}exp(-\frac{(y-μ_k)^2}{2σ_k^{2}})$ (2)

称为第k个分模型。
一般混合模型可以由任意概率分布密度函数代替2中的高斯密度函数，现在只介绍最常用的高斯混合模型。

高斯混合模型参数估计的EM算法

假设观测数据 $y_1,y_2……y_N$由高斯混合模型生成，
$P(y|θ)=\displaystyle\sum_{k=1}^{K}α_kφ(y|θ_k)$

其中 $θ=(α_1,α_2…α_K；θ_1,θ_2…θ_K)$，我们用EM算法估计高斯混合模型的参数 $θ$

1明确隐变量，写出完全数据的对数似然函数

可以设想观测数据 $y_j$,j=1,2……N，是这样产生的：
1）首先依概率 $α_k$选择第k个高斯分布分模型 $φ(y|θ_k)$

2）然后依第k个分模型的概率分布 $φ(y|θ_k)$生成观测数据 $y_j$

这时，观测数据 $y_j$时已知的，反映观测数据 $y_j$来自第k个分模型的数据时未知的。以变量 $γ_{jk}$表示。

隐变量 $γ_{jk}$，他的取值只能是1或者0
1）当第j个观测变量来自第k个高斯分布时，隐变量 $γ_{jk}$=1
2）当第j个观测变量不是来自第k个高斯分布时，隐变量 $γ_{jk}$=0

那么对于每一个观测数据 $y_j$,都会对应一个向量变量 $Γ_i=(γ_{j1},γ_{j2}…γ_{jK})$
其中只有一个分量是1，其他分量全为0
$\displaystyle\sum_{k=1}^{K}γ_{jk}=1$

$p(Γ_i)=∏α_k^{γ_{jk}}$ k=1,2,……K

其中，K为高斯分布的个数， $α_k$为第k个高斯分量的权值，因为观测数据来自各个高斯分布是相互独立的，而 $α_k$刚好可以看做观测数据来自第k个高斯分布的概率，因此可以用上式求 $p(Γ_i)$

有了观测数据 $y_j$以及 $γ_{jk}$，那么完全数据为 $(y_j,γ_{j1},γ_{j2}…γ_{jK})$

完全数据似然函数：
对于观测数据 $y_j$,当已知其是哪一个高斯分布生成的之后，其服从的概率分布为：
$p(y_j|γ_{jk}=1;θ)=φ(y|θ_k)$
由于观测数据从哪个高斯分布生成这个事件之间是相互独立的，因此可以写成

$p(y_i|Γ_i;θ)=∏φ(y_j|θ_k)^γ_{jk}$ k=1,2……K

由 $p(Γ_i)=∏α_k^{γ_{jk}}$ k=1,2,……K

两式相乘得到单个完全观测数据的似然函数：
$p(y_i,Γ_j;θ)=∏α_k^{γ_{jk}}φ(y_j|θ_k)^{γ_{jk}}$

最终得到所有观测数据的完全似然函数为：

$p(y,Γ_j;θ)=∏∏α_k^{γ_{jk}}φ(y_j|θ_k)^{γ_{jk}}$ 其中 j=1,2……N,k=1,2……K

取对数，得到对数似然函数为：

$lnp(y,Γ_j;θ)=\displaystyle\sum_{j=1}^{N}\displaystyle\sum_{k=1}^{K}(γ_{jk}lnα_k+γ_{jk}lnφ(y_j|θ_k))$

$φ(y|θ_k)=\frac{1}{\sqrt{2π}σ_k}exp(-\frac{(y-μ_k)^2}{2σ_k^{2}})$

假设，我们已经知道了隐变量 $γ_{jk}$的取值，对上面得到的似然函数分别对 $μ_k，σ_k$求偏导并令其为0，得到：

$μ_k=\frac{\displaystyle\sum_{j=1}^{N}\displaystyle\sum_{k=1}^{K}γ_{jk}y_j}{\displaystyle\sum_{j=1}^{N}\displaystyle\sum_{k=1}^{K}γ_{jk}}$

$σ_k=\frac{\displaystyle\sum_{j=1}^{N}\displaystyle\sum_{k=1}^{K}γ_{jk}(y_j-μ_k)^2}{\displaystyle\sum_{j=1}^{N}\displaystyle\sum_{k=1}^{K}γ_{jk}}$

由于上面两式的第二个求和符号是对k=1,2……K求和，而在求和过程中 $γ_{jk}$只有一次取到1，其他都是0，因此上面两个式子可以简化为：

$μ_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}y_j}{\displaystyle\sum_{j=1}^{N}γ_{jk}}$

$σ_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}(y_j-μ_k)^2}{\displaystyle\sum_{j=1}^{N}γ_{jk}}$

现在参数中还有一个 $α_k$没有求。
$α_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}}{N}$

隐变量的估计公式：

需要求 $γ_{jk}$
根据EM算法，现在需要通过当前参数的取值得到隐变量的估计公式，即隐变量的期望的表达形式。
即求解 $E(γ_{jk}|y,θ)$

$E(γ_{jk}|y,θ)=p(γ_{jk}=1|y,θ)$

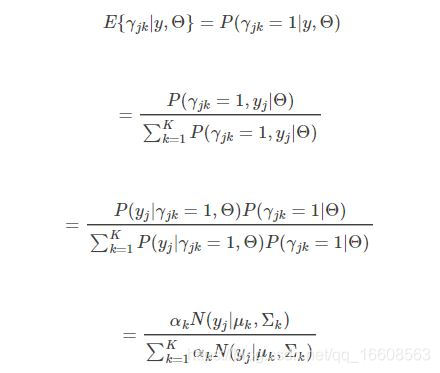
高斯混合模型参数估计EM算法流程

输入：观测数据 $y_1,y_2……y_n$,高斯混合模型
输出：高斯混合模型参数

1）取参数的初始值开始迭代
2）E步：依据当前的模型参数，计算分模型k对观测数据 $y_j$的响应度

$γ_{jk}=\frac{α_kφ(y|θ_k)}{\displaystyle\sum_{k=1}^{K}α_kφ(y|θ_k)}$

3)M步：计算新一轮迭代的模型参数

$μ_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}y_j}{\displaystyle\sum_{j=1}^{N}γ_{jk}}$

$σ_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}(y_j-μ_k)^2}{\displaystyle\sum_{j=1}^{N}γ_{jk}}$

$α_k=\frac{\displaystyle\sum_{j=1}^{N}γ_{jk}}{N}$

4）重复2）和3），知道收敛。