高斯过程 (Gaussian Process)

本博客转载自https://blog.csdn.net/u010016927/article/details/76856036

**针对机器学习的高斯过程（Gaussian Process for Machine Learning，即GPML）**是一个通用的监督学习方法，主要被设计用来解决回归问题。它可以拓展为概率分类（probability classification），但是在当前的实现中，这只是回归练习中的一个后续处理。

GPML的优势如下：

预测是对观察值的插值（至少在普通相关模型上）；
预测是带有概率的（Gaussian）。所以可以用来计算经验置信区间和超越概率以便对感兴趣的区域重新拟合（在线拟合，自适应拟合）预测；
多样性：可以指定不同的线性回归模型 linear regression model 和相关模型 correlation models。它提供了普通模型，但也能指定其它静态的自定义模型。

GPML的缺点如下：

不是稀疏的，它使用全部的样本/特征信息来做预测；
多维度空间下会变得低效，即当特征数量超过几十个，它可能确实会表现很差，而且计算效率下降；
分类只是一个后处理过程，意味着要建模，首先需要提供试验的完整浮点精度标量输出 $y$ 来解决回归问题。

要感谢高斯的预测的属性，已经有了广泛的应用，比如：最优化和概率分类。

Examples

1. 用一个回归样例来开场

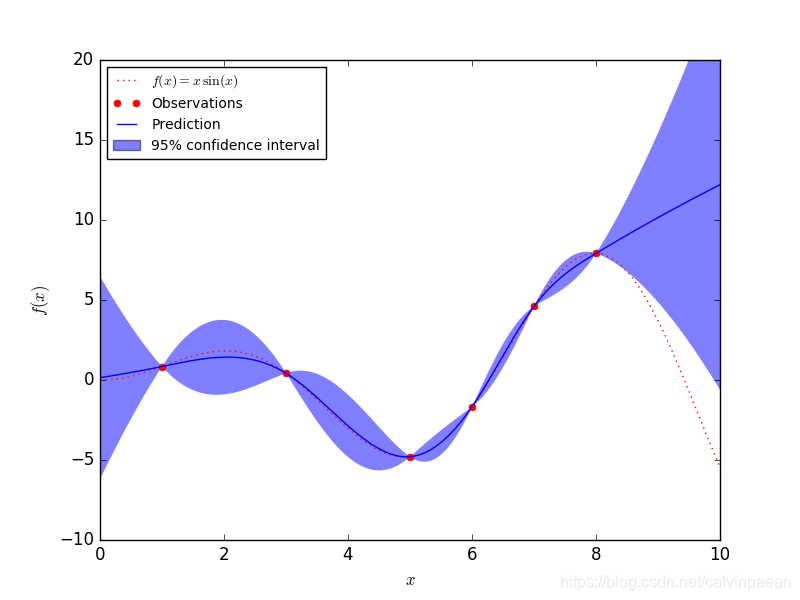
比如说，我们要代替函数:math: $g(x) = x sin(x)$ 。首先，要在一系列设计好的试验上对这个函数求值。然后，我们定义了一个Gaussian Process模型，它的回归模型和相关模型可能会通过附加的 $kwargs$ 来指明，并调用模型来拟合数据。根据实例提供的参数的数量，拟合程序可能依靠参数的最大似然估计或者是就使用给定的参数本身。

在这里插入图片描述

>>> import numpy as np
>>> from sklearn import gaussian_process
>>> def f(x):
...     return x * np.sin(x)
>>> X = np.atleast_2d([1., 3., 5., 6., 7., 8.]).T
>>> y = f(X).ravel()
>>> x = np.atleast_2d(np.linspace(0, 10, 1000)).T
>>> gp = gaussian_process.GaussianProcess(theta0=1e-2, thetaL=1e-4, thetaU=1e-1)
>>> gp.fit(X, y)  
GaussianProcess(beta0=None, corr=<function squared_exponential at 0x...>,
        normalize=True, nugget=array(2.22...-15),
        optimizer='fmin_cobyla', random_start=1, random_state=...
        regr=<function constant at 0x...>, storage_mode='full',
        theta0=array([[ 0.01]]), thetaL=array([[ 0.0001]]),
        thetaU=array([[ 0.1]]), verbose=False)
>>> y_pred, sigma2_pred = gp.predict(x, eval_MSE=True)

2. 拟合噪声数据

当要拟合的数据有噪声时，高斯过程模型能够通过用指定每个点的噪声方差来使用。

Gaussian Process 接收一个 $nugget$ 参数，这个参数会被加到训练数据相关矩阵的对角线上: 一般来说，这是Tikhonov正则化的其中一种类型。在平方指数(squared-exponential SE)相关函数的特殊情形下，这个正则相当于是指定了输入的误差方差。即

$nugget_i = \left[ \frac{\sigma_i}{y_i} \right]^2$

在 $nugget$ 和 $corr$ 设置合适的情况下，高斯过程可以鲁棒地从噪声数据中恢复出一个基本函数：
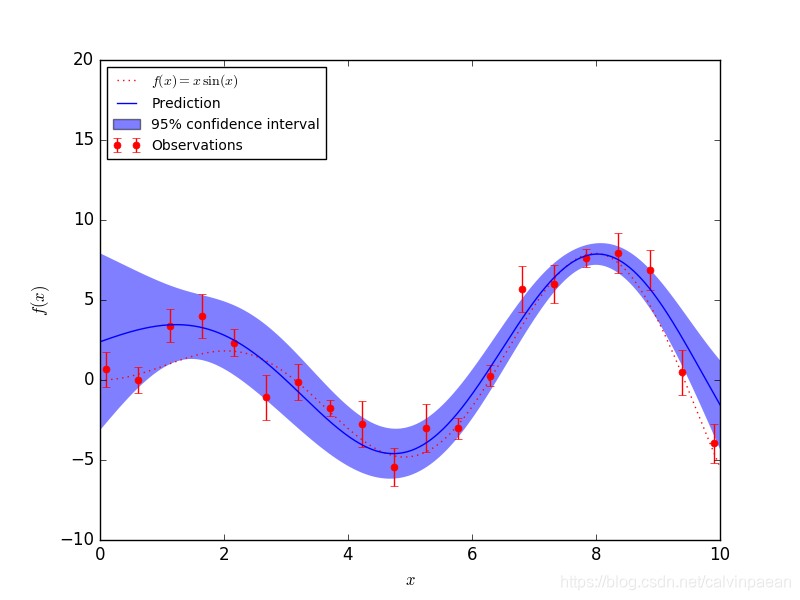
在这里插入图片描述

其它样例：

Gaussian Processes classification example: exploiting the probabilistic output

数学公式

1. 初始假设

假设一个人要对一个计算机实验的输出建模，比如一个数学函数：

$g: \mathbb{R}^{n_{features}} \rightarrow \mathbb{R}$
$X \rightarrow y = g(X)$

GPML 开始会假设这个函数是高斯过程 $G$ 的一个条件样本轨道，而 $G$ 另外被假定为下面这样：

$G(X) = f(X)^T\beta + Z(X)$

这里 $f(X)^T\beta$ 是一个线性回归模型，而 $Z(X)$ 是一个零均值的高斯过程，带一个全静态协方差函数
$C(X,X')=\sigma^2 R(|X-X'|)$

$\sigma^2$ 是它的方差，而 $R$ 是相关函数，只取决于每个样本间的相对距离的绝对值。可能有点feature-wise（这就是静态假设）。

根据这个公式，请注意，GPML不过是基本最小二乘线性回归的一种扩展：
$g(X) \sim f(X)^T\beta$

除了额外假设的一些样本间由相关函数决定的空间相干性（相关性）之外，实际上，普通最小二乘会假设相关模型 $R(|X-X'|)$ 是这样一个模型：当 $X=X'$ 时，为0；不相等时，为 $dirac^*$ (狄拉克)相关模型（有时候在 $Kriging$ 插值方法里被称作 $^*nugget$ 相关模型）

2. 最佳线性无偏预测（BLUP，The best linear unbiased prediction）

现在来推导样本轨道： $math:g$ 在观测条件下的最佳线性无偏预测：
$\hat G(X) = G(X|y_1 = g(X_1),\cdots,y_{n_{samples}} = g(X_{n_{samples}}))$

它是来源于它的“给定属性”。

它是线性的（观察值的一个线性组合）；
$\hat G(X) \equiv a(X)^T y$
它是无偏的；
$\mathbb{E}[G(X)-\hat G(X)] = 0$
它是最佳的（就均方误差来说）；
$\hat G(X)^* = \mathop{\arg\min}_{\hat G(X)} \mathbb{E}[(G(X)-\hat G(X))^2]$

所以最优权重向量 $a(X)$ 就是如下约束优化问题等式的解：
$a(X)^* = \mathop{\arg\min}_{\hat G(X)} \mathbb{E}[(G(X)-a(X)^T y)^2] \quad s.t. \quad \mathbb{E}[G(X)-a(X)^T y] = 0$

用拉格朗日方法重写这个约束优化问题，并进一步看，要满足一阶最优条件，就会得到一个用来预测的解析形式的表达式 — 完整的证明见参考文献。

最后, BLUP（最优线性无偏预测）表现为一个高斯随机变量，均值是：
$\mu_{\hat Y}(X) = f(X)^T \hat \beta + r(X)^T \gamma$

方差是：
$\sigma^2_{\hat Y}(X) = \sigma_Y^2 (1-r(X)^T R^{-1} r(X) + u(X)^T (F^T R^{-1} F)^{-1} u(X))$

这里我们引入：

相关矩阵，由自相关函数和内置的参数 $\theta$ 定义：
$R_{ij} = R(|X_i - X_j|,\theta), i,j=1,\cdots,m$
待预测点和DOE（实验设计）的一系列点之间交叉相关向量：
$r_i = R(|X-X_i|,\theta), i=1,\cdots,m$
回归矩阵（例如，当 $f$ 是一个多项式，就是范德蒙矩阵(Vandermonde)）：
$F_{ij} = f_i (X_j), i=1,\cdots, p, j=1,\cdots,m$
最小二乘法回归权重：
$\hat \beta = (F^T R^{-1} F)^{-1} F^T R^{-1} Y$
和这些向量：
$\gamma = R^{-1}(Y-F\hat \beta)$
$u(X) = F^T R^{-1} r(X) -f(X)$

切记，高斯过程预测器的概率结果是完全解析的，并主要依赖于基本的线性代数操作。

更准确来说，预测的均值是两个简单线性组合的和(点积)，方差需要是两个矩阵的逆，但相关矩阵可以使用Cholesky分解算法来分解。