讲这个之前,要先对模糊聚类和基于概率模型的聚类有个大体的认识。不清楚的同学可以参考下Jiawei的书去看一看,或者看看我的这篇文章。
数据挖掘:概念与技术(第三版)之第十一章的学习记录
OK,这里假设,大家已经有了上面我提到的先验知识。
GMM 和 k-means 很像。不过 GMM 是学习出一些概率密度函数来(所以 GMM 除了用在 clustering 上之外,还经常被用于 density estimation ),简单地说,k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了,而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率,又称作软聚类 。
而得出一个概率有很多好处,因为它的信息量比简单的一个结果要多。比如,我可以把这个概率转换为一个 score ,表示算法对自己得出的这个结果的把握。也许我可以对同一个任务,用多个方法得到结果,最后选取“把握”最大的那个结果;另一个很常见的方法是在诸如疾病诊断之类的场所,机器对于那些很容易分辨的情况(患病或者不患病的概率很高)可以自动区分,而对于那种很难分辨的情况,比如,49% 的概率患病,51% 的概率正常,如果仅仅简单地使用 50% 的阈值将患者诊断为“正常”的话,风险是非常大的,因此,在机器对自己的结果把握很小的情况下,会“拒绝发表评论”,而把这个任务留给有经验的医生去解决。如果有同学学习过贝叶斯网络,会发现GMM和其有相似之处。
我们知道,在机器学习中,一个学习算法一定会有一个偏执假设,而且这个偏执假设还要合理。(不清楚的可以回翻一下西瓜书)。
那么在GMM中,它的一个合理的偏执假设就是:就是假设数据服从混合高斯分布。换句话说,数据可以看作是从K个高斯分布中生成出来的。
那么这里就会有一个问题,我们为什么要假设数据集是服从高斯分布呢?为什么不是服从其他分布呢?
实际上,确实是可以的。因为不管是什么分布,只要K取得足够大,这个XX 混合模型就会变得足够复杂,就能逼近任意连续的概率密度分布。
而我们之所以选择高斯分布,纯粹是因为它在计算上有一些很好的性质。
我们先来看一下,单高斯分布模型GSM
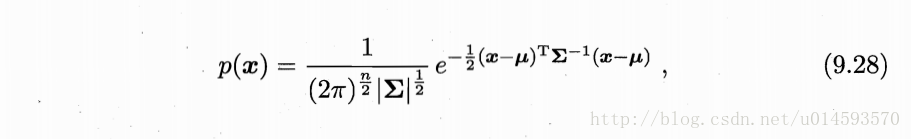
在这个模型中,x是维度为d的列向量,u是模型期望,Σ是模型方差。
在实际应用中u通常用样本均值来代替,Σ通常用样本方差来代替。这样的话,我们就很容易判断一个样本x是否属于类别C。因为每个类别都有自己的u和Σ,因此,我们只需要把x代入上式,当概率密度P(x)大于一定阈值时,我们就认为x属于C类。
而每个 GMM 由 K 个单高斯分布模型分布(Gaussian)组成的,我们把每个 Gaussian 称为一个“Component”,这些 Component 线性加成在一起就组成了 GMM 的概率密度函数:
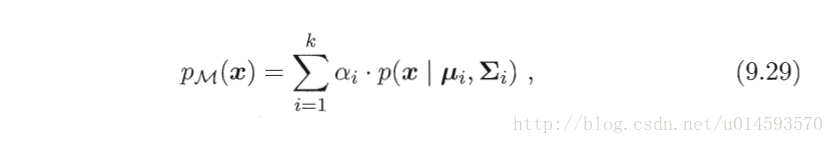
根据上面的式子,如果我们要从 GMM 的分布中随机地取一个点的话,实际上可以分为两步:首先随机地在这 K 个 Component 之中选一个,每个 Component 被选中的概率实际上就是它的系数 α,选中了 Component 之后,再单独地考虑从这个 Component 的分布中选取一个点就可以了(考虑被选中的component的概率密度函数)。而到了这里已经回到了普通的 Gaussian 分布,转化为了已知的问题。
那么如何用 GMM 来做聚类呢?
其实很简单,现在我们有了数据,假定它们是由 GMM 生成出来的,那么我们只要根据数据推出 GMM 的概率分布来就可以。(有看过我上面文章的同学,应该对这句话很熟悉),然后 GMM 的 K 个 Component 实际上就对应了 K 个 cluster 了(根据数据来推算概率密度通常被称作 density estimation )。
特别地,当我们在已知(或假定)了概率密度函数的形式,而要估计其中的参数的过程被称作“参数估计”(已知模型,要求有最大可能生成这个模型的参数,这很显然用到了 极大似然估计法)
现在假设我们有 N 个数据点,并假设它们服从某个分布(记作 p(x) ),现在要确定里面的一些参数的值,例如,在 GMM 中,我们就需要确定
那么,经过上面的操作后,对数似然函数为:
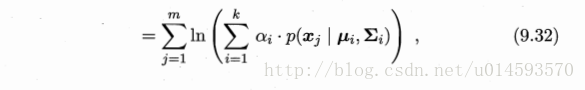
由于在对数函数里面又有累加,所以我们没法直接用求导解方程的办法直接求得最大值。为了解决这个问题,我们采取之前从 GMM 中随机选点的办法:分成两步,实际上也就类似于 K-means 的两步。
1、估计数据由每个 Component 生成的概率(并不是每个 Component 被选中的概率);(E步)
2、估计每个 Component 的参数;(M步)
3、迭代。
OK,至此,GMM已经讲解完毕。
当然,在这里旨在理清思路,省略了很多公式。而这些公式在周志华老师的书上全部都有,因此这里也不在重复赘述了。
参考文章
机器学习-周志华
聚类算法之高斯混合模型
EM及高斯混合模型