机器学习（十四）-GMM混合高斯模型(Gaussian mixture model)算法及Python实例

原创不易，转载前请注明博主的链接地址：Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境：
运行平台： Windows
Python版本： Python3.x
IDE： PyCharm
　

一什么是Gaussian mixture model

高斯混合模型，英文全称：Gaussian mixture model，简称GMM。高斯混合模型就是用高斯概率密度函数（二维时也称为：正态分布曲线）精确的量化事物，将一个事物分解为若干基于高斯概率密度函数行程的模型。这句话看起来有些深奥，这样去理解，事物的数学表现形式就是曲线，其意思就是任何一个曲线，无论多么复杂，我们都可以用若干个高斯曲线来无限逼近它，这就是高斯混合模型的基本思想。那么下图表示的就是这样的一个思想。
111
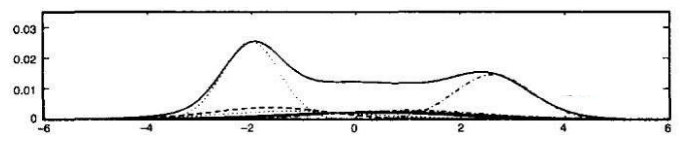
对于上图，换一种方式理解，曲线是模拟一组数据的结果，而这些数据分布情况如下图所示。那么此时GMM模拟出的曲线就有了现实的意义，这时就可以用构造好的GMM模型来表达这些数据，相比于存储数据，使用GMM中的参数来表达数据要方便简单的多，并且是数学上有完整的表达式。
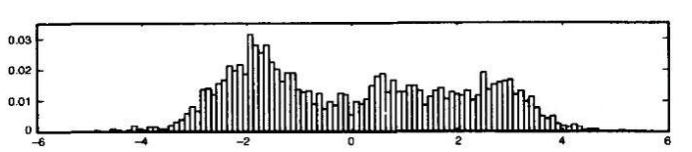
在这里插入图片描述
反过来思考，假如先拿到的是数据分布图，知道了数据的分布情况. 如何用曲线和数学表达式来逼近模拟它呢？答：用高斯混合模型来做!!!而混合高斯的曲线是由若干个单高斯函数叠加而成的。以上就是高斯混合模型的基本概念。
实际上，混合高斯就是通过求解多个单高斯模型，并通过一定的权重将多个单高斯模型融合成一个模型，即最终的混合高斯模型。一般化的描述为：假设混合高斯模型由K个高斯模型组成（即数据包含K个类），则GMM的概率密度函数如下：
在这里插入图片描述
其中，

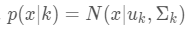
是第k个高斯模型的概率密度函数，可以看成选定第k个模型后，该模型产生x的概率；p(k)=πk 是第k个高斯模型的权重，称作选择第k个模型的先验概率，且满足

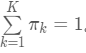
实际上，GMM的目的就是找到一个合适的高斯分布（也就是确定高斯分布的参数μ,Σ），使得这个高斯分布能产生这组样本的可能性尽可能大（即：拟合样本数据）。高斯混合模型也被视为一种聚类方法，是机器学习中对“无标签数据”进行训练得到的分类结果。其分类结果由概率表示，概率大者，则认为属于这一类。

二 Gaussian mixture model内容介绍

怎么去实现Gaussian mixture model呢？最开始的想法肯定是Log-Likelihood Function，因为这个方法在求最优化问题时是常用的手段。那最大化对数似然函数（log-likelihood function）的意义是什么呢？

2.1 最大化对数似然函数（log-likelihood function）的意义

首先直观化地解释一下最大化对数似然函数要解决的是什么问题。
假设我们采样得到一组样本yt ,而且知道变量Y服从高斯分布（本文只提及高斯分布，其他变量分布模型类似），数学形式表示为Y∼N(μ,Σ)。采样的样本如下图所示，我们的目的就是找到一个合适的高斯分布（也就是确定高斯分布的参数μ,Σ），使得这个高斯分布能产生这组样本的可能性尽可能大。
那怎么找到这个合适的高斯分布呢（在如下图中的表示就是1~4哪个分布较为合适）？这时候似然函数就闪亮登场了。
　

似然函数数学化：设有样本集Y=y1,y2…yN ，p( $y_n$ ∣μ,Σ)是高斯分布的概率分布函数，表示变量Y= $y_n$ 的概率。假设样本的抽样是独立的，那么我们同时抽到这N个样本的概率是抽到每个样本概率的乘积，也就是样本集Y的联合概率。此联合概率即为似然函数：
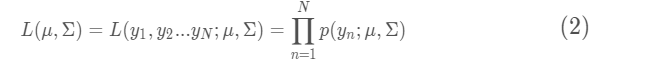
在这里插入图片描述
对式子(2)进行求导并令导数为0（即最大化似然函数，一般还会先转化为对数似然函数再最大化），所求出的参数就是最佳的高斯分布对应的参数。
　　所以最大化似然函数的意义就是：通过使得样本集的联合概率最大来对参数进行估计，从而选择最佳的分布模型。
　　对于上图产生的样本用最大化似然函数的方法，最终可以得到序号1对应的高斯分布模型是最佳的模型。

2.2 尝试用最大化对数似然函数（log-likelihood function）解决GMM

既然已经介绍了最大化对数似然函数（log-likelihood function)，那么接着尝试这用log-likelihood function来解决GMM。看看是否行得通。
解GMM模型，实际上就是确定GMM模型的参数(μ,Σ,π) ，使得由这组参数确定的GMM模型最有可能产生采样的样本。要利用极大似然估计求解模型最重要的一步就是求出似然函数，即样本集出现的联合概率。而对于混合高斯模型，如何求解某个样本 $y_t$ 的概率？显然我们得先知道这个样本来源于哪一类高斯模型，然后求这个高斯模型生成这个样本的概率p( $y_t$ ) ,这时就要引入隐变量了先引入一个隐变量 $\gamma$ 。它是一个K维二值随机变量，在它的K维取值中只有某个特定的元素 $\gamma_t$ 的取值为1，其它元素的取值为0。实际上，隐变量描述的就是：每一次采样，选择第k个高斯模型的概率，故有：
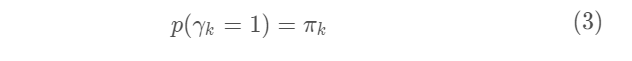
在这里插入图片描述
直接给出对数似然函数表示: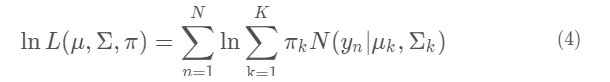
然后求导，令导数为0，就可以得到模型参数(μ,Σ,π) 。
　　然而仔细观察可以发现，对数似然函数里面，对数里面还有求和。实际上没有办法通过求导的方法来求这个对数似然函数的最大值。此时，就需要借助EM算法来解决此问题了

2.3 极大似然估计与EM算法适用问题分析

在这里插入图片描述

如果我们已经清楚了某个变量服从的高斯分布，而且通过采样得到了这个变量的样本数据，想求高斯分布的参数，这时候极大似然估计可以胜任这个任务；而如果我们要求解的是一个混合模型，只知道混合模型中各个类的分布模型（譬如都是高斯分布）和对应的采样数据，而不知道这些采样数据分别来源于哪一类（隐变量），那这时候就可以借鉴EM算法。EM算法可以用于解决数据缺失的参数估计问题（隐变量的存在实际上就是数据缺失问题，缺失了各个样本来源于哪一类的记录）。
下面将介绍EM算法的两个步骤：E-step(expectation-step，期望步)和M-step(Maximization-step,最大化步);

2.4 EM（xceptation-Maximization Algorithm）解决GMM

EM算法可以用于解决数据缺失的参数估计问题（隐变量的存在实际上就是数据缺失问题，缺失了各个样本来源于哪一类的记录）。

2.4.1 定义隐变量

引入隐变量 $y_jk$ ，它的取值只能是1或者0。

取值为1：第j个观测变量来自第k个高斯分量
取值为0：第j个观测变量不是来自第k个高斯分量

那么对于每一个观测数据 $y_j$ 都会对应于一个向量变量, $Γ_j$ ={ $γ_j1$ ,…, $γ_jK$ }，那么有：
在这里插入图片描述
其中，K为GMM高斯分量的个数， $α_k$ 为第k个高斯分量的权值。因为观测数据来自GMM的各个高斯分量相互独立，而 $α_k$ 刚好可以看做是观测数据来自第k个高斯分量的概率，因此可以直接通过连乘得到整个隐变量 $Γ_j$ 的先验分布概率。

2.4.2 得到完全数据的似然函数

对于观测数据 $y_j$ ,当已知其是哪个高斯分量生成的之后，其服从的概率分布为：
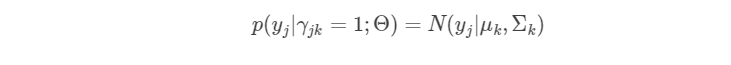
在这里插入图片描述
由于观测数据从哪个高斯分量生成这个事件之间的相互独立的，因此可以写为：

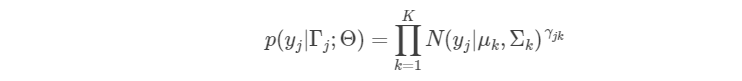
这样我们就得到了已知 $Γ_j$ 的情况下单个观测数据的后验概率分布。结合之前得到的 $Γ_j$ 的先验分布，则我们可以写出单个完全观测数据的似然函数为：
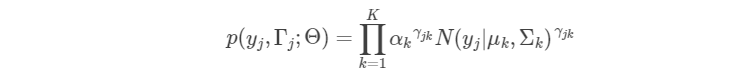
在这里插入图片描述
取对数，得到对数似然函数为：

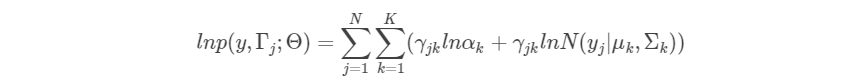
2.4.3 得到各个高斯分量的参数计算公式

首先，我们将上式中的lnN( $y_j$ | $μ_k$ , $Σ_k$ )根据单高斯的向量形式的概率密度函数的表达形式展开：
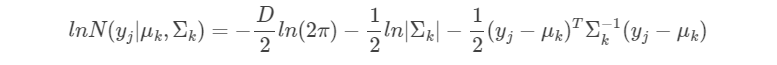
在这里插入图片描述
假设我们已经知道隐变量 $γ_jk$ 的取值，对上面得到的似然函数分别对 $α_k$ 和 $Σ_k$ 求偏导并且偏导结果为零，可以得到：

现在参数空间中剩下一个 $α_k$ 还没有求。这是一个约束满足问题，因为必须满足约束 $Σ_k=1^K$ $α_k$ =1。我们使用拉格朗日乘子法结合似然函数和约束条件对 $α_k$ 求偏导，可以得到：
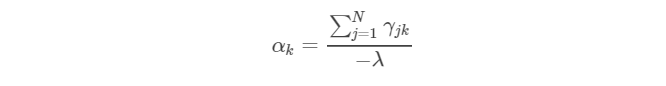
在这里插入图片描述
将上式的左右两边分别对k=1…K求和，可以得到：

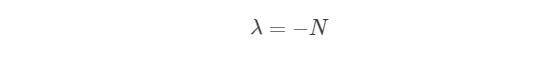
在这里插入图片描述
将λ代入，最终得到：

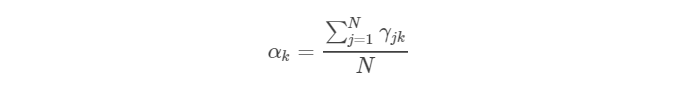
至此，我们在隐变量已知的情况下得到了GMM的三种类型参数的求解公式。

2.4.4得到隐变量的估计公式

根据EM算法，现在我们需要通过当前参数的取值得到隐变量的估计公式也就是说隐变量的期望的表达形式。即如何求解E{ $γ_jk$ |y,Θ}。
在这里插入图片描述

三 Gaussian mixture model的Python实现

在聚类中，k-means聚类模型简单易懂，但其简单性导致其应用中存在实际挑战。具体而言，k-means的非概率特性及简单地计算点与类蔟中心的欧式距离来判定归属，会导致其在许多真实的场景中性能较差。接下来探讨高斯混合模型(GMMs)，其可以看成k-means的延伸，更可以看成一个强有力的估计工具，而不仅仅是聚类。

3.1 GMM和K-means直观对比

首先看一下两者的过程：
GMM：

先计算所有数据对每个分模型的响应度
根据响应度计算每个分模型的参数
迭代

K-means：

先计算所有数据对于K个点的距离，取距离最近的点作为自己所属于的类
根据上一步的类别划分更新点的位置（点的位置就可以看做是模型参数）
迭代

可以看出GMM和K-means还是有很大的相同点的。GMM中数据对高斯分量的响应度就相当于K-means中的距离计算，GMM中的根据响应度计算高斯分量参数就相当于K-means中计算分类点的位置。然后它们都通过不断迭代达到最优。不同的是：GMM模型给出的是每一个观测点由哪个高斯分量生成的概率，而K-means直接给出一个观测点属于哪一类。

3.2 GMM的Python实现

3.2.1 GMM的动机：K-means的弱点

我们看下k-means的缺陷，思考下如何提高聚类模型。k-means的作用就是，给定简单，易于分类的数据，k-means能找到合适的聚类结果。
举例而言，假设有些简单的数据点，k-means算法能以某种方式很快地将它们聚类，跟我们肉眼分辨的结果很接近：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
# Plot the data with K Means Labels
from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit(X).predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis')
plt.show()

结果：

从直观的角度来看，期望聚类分配时，某些点比其他的更确定：举例而言，中间两个聚类之间似乎存在非常轻微的重叠，这样我们可能对这些数据点的分配没有完全的信心。不幸的是，k-means模型没有聚类分配的概率或不确定性的内在度量（尽管可能使用bootstrap 的方式来估计这种不确定性）。为此，我们必须考虑泛化这种模型。
k-means模型的一种理解思路是，它在每个类蔟的中心放置了一个圈（或者，更高维度超球面)，其半径由聚类中最远的点确定。该半径充当训练集中聚类分配的一个硬截断：任何圈外的数据点不被视为该类的成员。我们可以使用以下函数可视化这个聚类模型：

from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting

def plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None):
    labels = kmeans.fit_predict(X)

    # plot the input data
    ax = ax or plt.gca()
    ax.axis('equal')
    ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)

    # plot the representation of the KMeans model
    centers = kmeans.cluster_centers_
    radii = [cdist(X[labels == i], [center]).max()
             for i, center in enumerate(centers)]
    for c, r in zip(centers, radii):
        ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))

kmeans = KMeans(n_clusters=4,random_state=0)
plot_kmeans(kmeans,X)
plt.show()

结果：

观察k-means的一个重要发现，这些聚类模式必须是圆形的。k-means没有内置的方法来计算椭圆形或椭圆形的簇。因此，举例而言，假设我们将相同的数据点作变换，这种聚类分配方式最终变得混乱：

from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import numpy as np
# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))


def plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None):
    labels = kmeans.fit_predict(X)

    # plot the input data
    ax = ax or plt.gca()
    ax.axis('equal')
    ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)

    # plot the representation of the KMeans model
    centers = kmeans.cluster_centers_
    radii = [cdist(X[labels == i], [center]).max()
             for i, center in enumerate(centers)]
    for c, r in zip(centers, radii):
        ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))

kmeans = KMeans(n_clusters=4,random_state=0)
plot_kmeans(kmeans,X_stretched)
plt.show()

结果：

肉眼观察，我们分别出这些变换过的集群是非圆的，因此圆形模式的聚类很难拟合。然而，k-means不够灵活解释这一点，尝试强行将数据点分配到四个圆形类别。这将导致聚类分配的混乱，其生成的圆形重叠：具体见图的右下角。有人会想到使用PCA(In Depth: Principal Component Analysis)预处理数据来解决这种特殊情况，但实际上并不能保证这种处理方式能使数据分布成圆簇状。
k-means的两大缺陷 – 聚类形状的不够灵活和缺少聚类分配的概率值，
意味着许多数据集(尤其是低维数据集)，可能不会有预期的效果。
你也许想到通过泛化k-means模型来克服这些缺点：譬如，你可以在数据点聚类分配时，利用每个点到各个类簇的中心的距离来衡量不确定性，而不是仅仅关注最接近的。你也可以想象允许聚类的边界是椭圆而不是圆，以便更好地拟合非圆形的类簇。事实证明，高斯混合模型有着这两种基本的优点。

3.2.2 高斯混合模型GMM的Python应用

高斯混合模型（GMM）试图找到一个多维高斯概率分布的混合，以模拟任何输入数据集。在最简单的情况下，GMM可用于以与k-means相同的方式聚类。

from sklearn import mixture
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting

gmm = mixture.GaussianMixture(n_components=4).fit(X)
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis')
plt.show()

结果：

但因为GMM包含概率模型，因此可以找到聚类分配的概率方式 - 在Scikit-Learn中，通过调用predict_proba方法实现。它将返回一个大小为[n_samples, n_clusters]的矩阵，用于衡量每个点属于给定类别的概率：

from sklearn import mixture
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
probs = gmm.predict_proba(X)
print(probs[:5].round(3))

结果：
[[0.469 0. 0. 0.531]
[0. 1. 0. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 1. 0. 0. ]]

本质上说，高斯混合模型与k-means非常相似：它使用期望-最大化的方式，定性地执行以下操作：

选择位置和形状的初始猜想
重复直到收敛
E步骤：对于每个点，计算其属于每个类别的概率权重
M步骤：对于每个类别，使用E步算出的权重，根据所有数据点，更新其位置，规范化和形状
结果是，每个类别不是被硬边界的球体界定，而是平滑的高斯模型。正如在k-means的期望-最大方法一样，这种算法有时可能会错过全局最优解，因此在实践中使用多个随机初始化。

让我们创建一个函数，通过基于GMM输出，绘制椭圆来帮助我们可视化GMM聚类的位置和形状：

from sklearn import mixture
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
from matplotlib.patches import Ellipse
import numpy as np

# Generate some data
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
                       cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting

def draw_ellipse(position, covariance, ax=None, **kwargs):
    """Draw an ellipse (椭圆)with a given position and covariance"""
    ax = ax or plt.gca()

    # Convert covariance to principal axes
    if covariance.shape == (2, 2):
        U, s, Vt = np.linalg.svd(covariance)
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
        width, height = 2 * np.sqrt(s)
    else:
        angle = 0
        width, height = 2 * np.sqrt(covariance)

    # Draw the Ellipse
    for nsig in range(1, 4):
        ax.add_patch(Ellipse(position, nsig * width, nsig * height,
                             angle, **kwargs))

def plot_gmm(gmm, X, label=True, ax=None):
    ax = ax or plt.gca()
    labels = gmm.fit(X).predict(X)
    if label:
        ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
    else:
        ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
    ax.axis('equal')

    w_factor = 0.2 / gmm.weights_.max()
    i=0
    for  pos, covar, w in zip(gmm.means_, gmm.precisions_, gmm.weights_):
        if i<=3:
            draw_ellipse(pos, covar, alpha=w * w_factor)
            i=i+1

gmm = mixture.GaussianMixture(n_components=4, random_state=42)
plot_gmm(gmm, X)
plt.show()

结果：

3.2.3 选择协方差类型

如果看了之前拟合的细节，将covariance_type选项在每个中都设置不同。该超参数控制每个类簇的形状的自由度；对于任意给定的问题，必须仔细设置。

默认值为covariance_type =“diag”，这意味着可以独立设置沿每个维度的类蔟大小，并将得到的椭圆约束为与轴对齐。
一个稍微简单和快速的模型是covariance_type =“spherical”，它约束了类簇的形状，使得所有维度都相等。尽管它并不完全等效，其产生的聚类将具有与k均值相似的特征。
更复杂且计算量更大的模型（特别是随着维数的增长）是使用covariance_type =“full”，这允许将每个簇建模为具有任意方向的椭圆。

对于一个类蔟，下图我们可以看到这三个选项的可视化表示：
在这里插入图片描述

四总结

下图梳理了高斯分布参数估计的逻辑流程。
　

下图梳理了混合高斯分布估计的逻辑流程。
　

相对比于高斯分布的参数估计，混合高斯分布的参数估计更加复杂。主要原因在于隐变量的存在。而为什么混合高斯分布的参数估计需要多次迭代循环进行？是因为EM算法中对于 $\gamma$ 的估计利用的是初始化或者第i步迭代的参数（μ^i,Σ ^i ,π ^i ),，这对于样本的分类划分是有误差的。所以它只能通过多次迭代优化寻找更佳的参数来抵消这一误差。

参考文章

1 详解EM算法与混合高斯模型(Gaussian mixture model, GMM)
2 高斯混合模型（GMM）及其EM算法的理解
3 高斯混合模型的终极理解
4 深度理解高斯混合模型（GMM）
5 [译] 高斯混合模型 — python教程