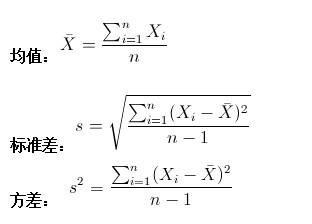写在前面:
Gaussian Mixture Model (GMM)。事实上,GMM 和 k-means 很像,不过 GMM 是学习出一些概率密度函数来(所以 GMM 除了用在 clustering 上之外,还经常被用于 density estimation ),简单地说,k-means 的结果是每个数据点被 assign 到其中某一个 cluster 了,而 GMM 则给出这些数据点被 assign 到每个 cluster 的概率,又称作 soft assignment 。
得出一个概率有很多好处,因为它的信息量比简单的一个结果要多,比如,我可以把这个概率转换为一个 score ,表示算法对自己得出的这个结果的把握。也许我可以对同一个任务,用多个方法得到结果,最后选取“把握”最大的那个结果;另一个很常见的方法是在诸如疾病诊断之类的场所,机器对于那些很容易分辨的情况(患病或者不患病的概率很高)可以自动区分,而对于那种很难分辨的情况,比如,49% 的概率患病,51% 的概率正常,如果仅仅简单地使用 50% 的阈值将患者诊断为“正常”的话,风险是非常大的,因此,在机器对自己的结果把握很小的情况下,会“拒绝发表评论”,而把这个任务留给有经验的医生去解决。
准备阶段
1.协方差
注:内容是http://pinkyjie.com/2010/08/31/covariance/(讲的太好了,一下子就理解了,对下面的高斯混合模型没啥帮助,我以为会用到的,哈哈)
统计学的基本概念
学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合X={X1,…,Xn}
很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
为什么需要协方差?
上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
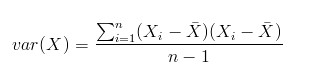
来度量各个维度偏离其均值的程度,标准差可以这么来定义:
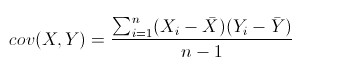
协方差的结果有什么意义呢?如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质,如:
协方差多了就是协方差矩阵
上一节提到的猥琐和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算n!(n−2)!∗2
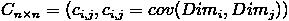
这个定义还是很容易理解的,我们可以举一个简单的三维的例子,假设数据集有{x,y,z}
可见,协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。
Matlab协方差实战
上面涉及的内容都比较容易,协方差矩阵似乎也很简单,但实战起来就很容易让人迷茫了。必须要明确一点,### 协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。这个我将结合下面的例子说明,以下的演示将使用Matlab,为了说明计算原理,不直接调用Matlab的cov函数。
首先,随机产生一个10*3维的整数矩阵作为样本集,10为样本的个数,3为样本的维数。
|
1
|
MySample = fix(rand(10,3)*50)
|
根据公式,计算协方差需要计算均值,那是按行计算均值还是按列呢,我一开始就老是困扰这个问题。前面我们也特别强调了,协方差矩阵是计算不同维度间的协方差,要时刻牢记这一点。样本矩阵的每行是一个样本,每列为一个维度,所以我们要### 按列计算均值。为了描述方便,我们先将三个维度的数据分别赋值:
|
1
2
3
|
dim1 = MySample(:,1);
dim2 = MySample(:,2);
dim3 = MySample(:,3);
|
计算dim1与dim2,dim1与dim3,dim2与dim3的协方差:
|
1
2
3
|
sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到 74.5333
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -10.0889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 -106.4000
|
搞清楚了这个后面就容易多了,协方差矩阵的对角线就是各个维度上的方差,下面我们依次计算:
|
1
2
3
|
std(dim1)^2 % 得到 108.3222
std(dim2)^2 % 得到 260.6222
std(dim3)^2 % 得到 94.1778
|
这样,我们就得到了计算协方差矩阵所需要的所有数据,调用Matlab自带的cov函数进行验证:
|
1
|
cov(MySample)
|
把我们计算的数据对号入座,是不是一摸一样?
Update:
今天突然发现,原来协方差矩阵还可以这样计算,先让样本矩阵中心化,即每一维度减去该维度的均值,使每一维度上的均值为0,然后直接用新的到的样本矩阵乘上它的转置,然后除以(N-1)即可。其实这种方法也是由前面的公式通道而来,只不过理解起来不是很直观,但在抽象的公式推导时还是很常用的!同样给出Matlab代码实现:
|
1
2
|
X = MySample - repmat(mean(MySample),10,1); % 中心化样本矩阵,使各维度均值为0
C = (X'*X)./(size(X,1)-1);
|
总结
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间,拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度,心中明确这个整个计算过程就会顺流而下,这么一来就不会迷茫了~
2.高斯函数(模型)
记得上次看高斯函数还是在高斯滤波和双边滤波的时候,现在再来提到都已经忘得差不多了。。。。
知道下面几个公式就可以了:
高斯一维函数:

高斯概率分布函数:

3.EM算法
本来打算在这里叙述的,感觉内容有点多,而且以后还会用到这个算法,还是另外开一篇博客叙述:http://www.cnblogs.com/wjy-lulu/p/7010258.html
4.混合高斯模型
注释:这里是http://blog.sina.com.cn/s/blog_54d460e40101ec00.html博客的内容,看了很多篇文章,感觉还是这篇讲的好,不是很深入但是把原理讲的很清楚。
高斯混合模型--GMM(Gaussian Mixture Model)
统计学习的模型有两种,一种是概率模型,一种是非概率模型。
所谓概率模型,是指训练模型的形式是P(Y|X)。输入是X,输出是Y,训练后模型得到的输出不是一个具体的值,而是一系列的概率值(对应于分类问题来说,就是输入X对应于各个不同Y(类)的概率),然后我们选取概率最大的那个类作为判决对象(软分类--soft assignment)。所谓非概率模型,是指训练模型是一个决策函数Y=f(X),输入数据X是多少就可以投影得到唯一的Y,即判决结果(硬分类--hard assignment)。
所谓混合高斯模型(GMM)就是指对样本的概率密度分布进行估计,而估计采用的模型(训练模型)是几个高斯模型的加权和(具体是几个要在模型训练前建立好)。每个高斯模型就代表了一个类(一个Cluster)。对样本中的数据分别在几个高斯模型上投影,就会分别得到在各个类上的概率。然后我们可以选取概率最大的类所为判决结果。
从中心极限定理的角度上看,把混合模型假设为高斯的是比较合理的,当然,也可以根据实际数据定义成任何分布的Mixture Model,不过定义为高斯的在计算上有一些方便之处,另外,理论上可以通过增加Model的个数,用GMM近似任何概率分布。
混合高斯模型的定义为:
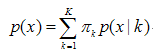
其中K 为模型的个数;πk为第k个高斯的权重;p(x / k) 则为第k个高斯概率密度,其均值为μk,方差为σk。对此概率密度的估计就是要求出πk、μk 和σk 各个变量。当求出p(x )的表达式后,求和式的各项的结果就分别代表样本x 属于各个类的概率。
在做参数估计的时候,常采用的是最大似然方法。最大似然法就是使样本点在估计的概率密度函数上的概率值最大。由于概率值一般都很小,N 很大的时候, 连乘的结果非常小,容易造成浮点数下溢。所以我们通常取log,将目标改写成:

也就是最大化对数似然函数,完整形式为:

一般用来做参数估计的时候,我们都是通过对待求变量进行求导来求极值,在上式中,log函数中又有求和,你想用求导的方法算的话方程组将会非常复杂,没有闭合解。可以采用的求解方法是EM算法——将求解分为两步:第一步,假设知道各个高斯模型的参数(可以初始化一个,或者基于上一步迭代结果),去估计每个高斯模型的权值;第二步,基于估计的权值,回过头再去确定高斯模型的参数。重复这两个步骤,直到波动很小,近似达到极值(注意这里是极值不是最值,EM算法会陷入局部最优)。具体表达如下:
注释:这是需要求得参数有两类:(每个模型权重W)(每个模型的参数),这是按照EM思想,首先假定(参数)把每个样本点分类计算(权重),然后通过分类的样本点计算新的(参数),接着对比假设参数和计算的参数是否符合精度,符合结束,不符合就继续上面的操作去迭代。
A、(E step)
对于第i个样本xi 来说,它由第k 个model 生成的概率为:
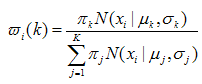
在这一步,假设高斯模型的参数和是已知的(由上一步迭代而来或由初始值决定)。
B、(M step)
C、重复上述两步骤直到算法收敛。
极大似然算法
本来打算把别人讲的好的博文放在上面的,但是感觉那个适合看着玩,我看过之后感觉懂了,然后实际应用就不会了。。。。
MLP其实就是用来求模型参数的,核心就是“模型已知,求取参数”,模型的意思就是数据符合什么函数,比如我们硬币的正反就是二项分布模型,再比如我们平时随机生成的一类数据符合高斯模型。。。
直接上公式:
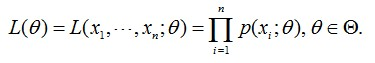
L(Θ) :联合概率分布函数,就是每个样本出现的概率乘积。
x1,x2,x3....xn : 样本
Θ : 模型的参数(比如高斯模型的两个参数:μ、σ)
p(xi ; Θ) : 第i个样本的概率模型
xi :第i个样本
平时使用的时候取对数,完全为了求解方便。(从后面可以看出求导方便):
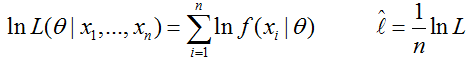
而 称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:
称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然,即:
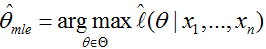
举例一:
举一个抛硬币的简单例子。 现在有一个正反面不是很匀称的硬币,如果正面朝上记为H,方面朝上记为T,抛10次的结果如下:
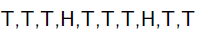
求这个硬币正面朝上的概率有多大?
很显然这个概率是0.2。现在我们用MLE的思想去求解它。我们知道每次抛硬币都是一次二项分布,设正面朝上的概率是 ,那么似然函数为:
,那么似然函数为:
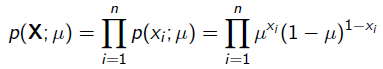
x=1表示正面朝上,x=0表示方面朝上。那么有:
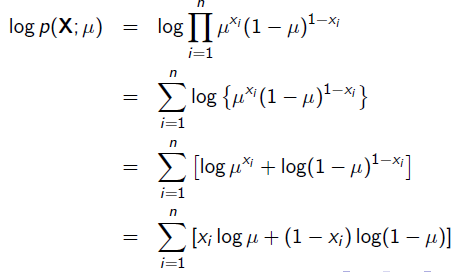
求导:
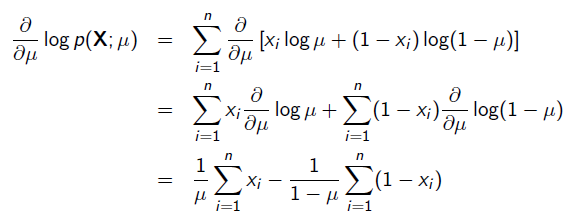
令导数为0,很容易得到:
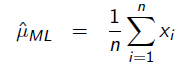
也就是0.2 。
举例二:
假如我们有一组连续变量的采样值(x1,x2,…,xn),我们知道这组数据服从正态分布,标准差已知。请问这个正态分布的期望值为多少时,产生这个已有数据的概率最大?
P(Data | M) = ?
根据公式:

可得:

对μ求导可得:

则最大似然估计的结果为μ=(x1+x2+…+xn)/n
举例三:
假设我们要统计全国人民的年均收入,首先假设这个收入服从服从正态分布,但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的收入。我们国家有10几亿人口呢?那么岂不是没有办法了?
不不不,有了极大似然估计之后,我们可以采用嘛!我们比如选取一个城市,或者一个乡镇的人口收入,作为我们的观察样本结果。然后通过最大似然估计来获取上述假设中的正态分布的参数。
有了参数的结果后,我们就可以知道该正态分布的期望和方差了。也就是我们通过了一个小样本的采样,反过来知道了全国人民年收入的一系列重要的数学指标量!
那么我们就知道了极大似然估计的核心关键就是对于一些情况,样本太多,无法得出分布的参数值,可以采样小样本后,利用极大似然估计获取假设中分布的参数值。
注:最大似然函数真的很简单,刚开始我也一头雾水。其实我们用的很多函数都可以说是一个最大似然函数,比如符合y = x2、y = kx。。。。都可以当做一个模型去求解一个极大似然函数,只不过我们得到的数据不符合这些模型而已。
大家有没有发现只要是求概率的问题,都会写出一个函数,这个函数其实就是最大似然函数,可以说是目标函数,也可以说是似然函数,把每个数据出现的概率相乘就是似然函数,再求对数,再求均值,再求最值,这就是极大似然了,就是一个名字而已!
EM算法概述
EM算法核心:猜(E-step),反思(M-step),重复;
先说说我自己对EM算法的理解:
问题一:
现在一个班里有50个男生,50个女生,且男生站左,女生站右。我们假定男生的身高服从正态分布 ,女生的身高则服从另一个正态分布:
。这时候我们可以用极大似然法(MLE),分别通过这50个男生和50个女生的样本来估计这两个正态分布的参数。
问题二:
但现在我们让情况复杂一点,就是这50个男生和50个女生混在一起了。我们拥有100个人的身高数据,却不知道这100个人每一个是男生还是女生。这时候情况就有点尴尬,因为通常来说,我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。但从另一方面去考量,我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。
问题二需要求解两个问题:
假设a=(第k个样本是男生还是女生)
假设b=(高斯模型的参数)
如果知道a,那用问题一的方法就可以求解b,如果知道b那也就可以分类a了,但是前提是两个都不知道。。。。比如y=x+1,现在让你求解x和y的值,怎么办?

总结:其实EM算法就是先通过假设的参数(不能太无厘头了)把数据进行分类,然后通过分类的数据计算参数,接着对比计算的参数和假设的参数是否满足精度,不满足就返回去,满足就结束。
EM算法使用简单,但是证明很麻烦,我感觉没必要去证明,会使用就好了,反正EM是一种思想,而不是像K-means等是一种算法。#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace cv::ml;
using namespace std;
int main(int argc, char** argv)
{
Mat src = imread("girl1.jpg");
if (src.empty())
{
printf("could not load iamge...\n");
return -1;
}
char* inputWinTitle = "input image";
namedWindow(inputWinTitle, CV_WINDOW_AUTOSIZE);
imshow(inputWinTitle, src);
// 初始化
int numCluster = 3;//分成三类
//分成的类的颜色从这里选择
const Scalar colors[] = {
Scalar(255, 0, 0),
Scalar(0, 255, 0),
Scalar(0, 0, 255),
Scalar(255, 255, 0)
};
int width = src.cols;
int height = src.rows;
int channels = src.channels();
int nsamples = width*height;//points用来保存所有的数据
Mat points(nsamples, channels, CV_64FC1);
Mat labels;//聚类后的标签
Mat result = Mat::zeros(src.size(), CV_8UC3);
// 图像RGB像素数据转换为样本数据
int index = 0;
for (int row = 0; row < height; row++)
{
for (int col = 0; col < width; col++)
{
index = row*width + col;
Vec3b rgb = src.at<Vec3b>(row, col);
//对像素的每一个通道进行赋值
points.at<double>(index, 0) = static_cast<int>(rgb[0]);
points.at<double>(index, 1) = static_cast<int>(rgb[1]);
points.at<double>(index, 2) = static_cast<int>(rgb[2]);
}
}
// EM Cluster Train
Ptr<EM> em_model = EM::create();
em_model->setClustersNumber(numCluster);//设置分类数
em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);//设置协方差矩阵的类型
em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));//设置停止条件
em_model->trainEM(points, noArray(), labels, noArray());//对数据进行em训练
/*
//第一种方式
// 对每个像素标记颜色与显示
for (int row = 0; row < height; row++)
{
for (int col = 0; col < width; col++)
{
index = row*width + col;
int label = labels.at<int>(index);//求出每一个像素属于哪一个标签
//对每一个像素通道进行赋值
result.at<Vec3b>(row, col)[0] = colors[label][0];
result.at<Vec3b>(row, col)[1] = colors[label][1];
result.at<Vec3b>(row, col)[2] = colors[label][2];
}
}
*/
//第二种方式 预言
Mat sample(channels, 1, CV_64FC1);//创建单个像素
int b = 0, g = 0, r = 0;
for (int row = 0; row < height; row++)
{
for (int col = 0; col < width; col++)
{
//将每一个通道的像素值取出来
b = src.at<Vec3b>(row, col)[0];
g = src.at<Vec3b>(row, col)[1];
r = src.at<Vec3b>(row, col)[2];
sample.at<double>(0) = b;
sample.at<double>(1) = g;
sample.at<double>(2) = r;
int response = cvRound(em_model->predict2(sample, noArray())[1]);
Scalar c = colors[response];
result.at<Vec3b>(row, col)[0] = c[0];
result.at<Vec3b>(row, col)[1] = c[1];
result.at<Vec3b>(row, col)[2] = c[2];
}
}
imshow("result", result);
waitKey(0);
return 0;
}
原图:

效果图:

参考:
1.http://blog.csdn.net/zouxy09/article/details/8537620(本博文的核心都来自这里,说的通俗易懂!)
2.http://www.cnblogs.com/sylvanas2012/p/5058065.html(最大似然的举例1)
3.http://blog.csdn.net/qq_18343569/article/details/49981507(最大似然的举例2)
4.https://www.zhihu.com/question/27976634/answer/154998358(EM算法的问题来源知乎,但是作者没有解决)
5.http://www.mamicode.com/info-detail-466443.html(用大白文叙述GMM,娱乐的看看还好)
6.http://blog.pluskid.org/?p=39(讲的很好)
7.http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html(高斯混合模型的EM算法推导公式,感兴趣可以看看,反正我没看)
8.http://www.jianshu.com/p/1121509ac1dc(还没来得及看的EM例子,排版很好,不知道内容)