机器学习 -- 线性回归（Linear Regression）原理及算法实现

1. 线性回归的原理

假设有一个数据集，希望通过一些特征 $x_{1}$ ,…, $x_{p}$ 预测目标变量 $y$ .最简单的模型是假设目标变量 $y$ 是这些特征的某个线性组合：

$y \approx a_{0} + a_{1}x_{1} + \cdot \cdot \cdot +a_{p}x_{p}$

记第 $i$ 组观测为 $(x_{1}^{(i)},..., x_{n}^{i}, y^{i})$ 。总共有 $n$ 组观测。

第 $i$ 组观测的预测值为 $\widehat{y}^{(i)} = a_{0} + a_{1}x_{1}^{(i)} + ... + a_{p}x_{p}^{(i)}$

我们将 $a_{0}, a_{1}, ....., a_{p}$ 视为参数， 最小化均方误差（Mean Squared Error）：

$L(a_{0}, a_{1}, ....., a_{p}) = \frac{1}{n}[(y^{(1)} - \widehat{y}^{(1)})^{2} + ... + (y^{(n)} - \widehat{y}^{(n)})^{2}]$

2. 算法

假设 $x_{0} = 1, x_{1}, ......, x_{p}$ 组成的数据矩阵 $X_{n\times (p+1)}$ 列满秩（full column rank)，即秩为（p+1）。则 $X^{T}X$ 是秩为（p+1）的方阵，因此可逆。并且最优的参数 $(a_{0}, a_{1}, ......, a_{p})$ 满足正规方程（normal equation）:

$X^{T}X\begin{bmatrix}a_{0}\\ a_{1}\\ ...\\ a_{p}\end{bmatrix} = X^{T}y$

因为 $X^{T}X$ 可逆，可以通过求解该线性系统得到待求的参数。当 $p$ 过大时，求解线性系统的效率就会很低，因此我们转而使用梯度下降（Gradient Descent）近似地估计参数。

3. Python实现

Python中的 scikit-learn 包可以进行线性回归模型的训练：scikit-learn线性回归模型文档

 print(__doc__)


    # Code source: Jaques Grobler
    # License: BSD 3 clause
    
    
    import matplotlib.pyplot as plt
    import numpy as np
    from sklearn import datasets, linear_model
    from sklearn.metrics import mean_squared_error, r2_score
    
    # Load the diabetes dataset
    diabetes = datasets.load_diabetes()
    
    
    # Use only one feature
    diabetes_X = diabetes.data[:, np.newaxis, 2]
    
    # Split the data into training/testing sets
    diabetes_X_train = diabetes_X[:-20]
    diabetes_X_test = diabetes_X[-20:]
    
    # Split the targets into training/testing sets
    diabetes_y_train = diabetes.target[:-20]
    diabetes_y_test = diabetes.target[-20:]
    
    # Create linear regression object
    regr = linear_model.LinearRegression()
    
    # Train the model using the training sets
    regr.fit(diabetes_X_train, diabetes_y_train)
    
    # Make predictions using the testing set
    diabetes_y_pred = regr.predict(diabetes_X_test)
    
    # The coefficients
    print('Coefficients: \n', regr.coef_)
    # The mean squared error
    print("Mean squared error: %.2f"
          % mean_squared_error(diabetes_y_test, diabetes_y_pred))
    # Explained variance score: 1 is perfect prediction
    print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
    
    # Plot outputs
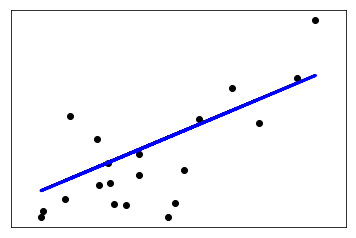
    plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
    plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
    
    plt.xticks(())
    plt.yticks(())
    
    plt.show()

输出：
Automatically created module for IPython interactive environment
Coefficients:
[938.23786125]
Mean squared error: 2548.07
Variance score: 0.47

LinearRegressionDemoPic.png-4.3kB

4. 共线性（Collinearity）

当数据矩阵 $X_{n\times(p+1)}$ 不是满秩时，正规方程中的 $X^{T}X$ 不可逆，任何满足正规方程的参数都能够最小化均方误差。满足要求的解有无限多个，因此得出的解容易过拟合（Overfiting）。这个问题又称为数据的共线性。
如果 $n \leqslant p$ ,则数据一定共线性。否则，数据很少精确地满足共线性。即使数据不是精确地满足共线性，也可能会非常接近列不满秩。此时 $X^{T}X$ 虽然可逆，但是数值求解其逆矩阵（Inverse Matrix）非常不稳定，这样得到的不稳定解也容易产生过拟合。

解决共线性的方法主要有两种。第一种是找出共线性的列并且删除其中一列直到数据列满秩。第二种是使用正则化（Regularization）。

5. 岭回归（Ridge Regression），Lasso回归和弹性网络（Elastic Net）回归

对于线性归回，正则化的两种是使用岭回归（Ridge Regression）或Lasso。
岭回归的思想是在原来的均方误差损失函数的基础上加上参数的 $l_{2}$ 范数平方作为惩罚项。新的损失函数是：

$L_{\lambda}(a_{0}, a_{1},..., a_{p}) = L(a_{0}, a_{1},...,a_{p}) + \frac{\lambda}{n}[a_{0}^{2} + a_{1}^{2} + ...+ a_{p}^{2}]$

类似原来的正规方程，新的方程为：

$(X^{T}X + \lambda I_{p+1})\begin{bmatrix} a_{0}\\ a_{1}\\ ...\\ a_{p}\end{bmatrix} = X^{T}y$

由于 $X^{T}X$ 一定是半正定（Positive Semi-definite）的，只要 $\lambda > 0, X^{T}X + \lambda I_{p+1}$ 的每一个特征值都不小于 $\lambda$ ,因此 $X^{T}X + \lambda I_{p+1}$ 是正定（Positive Definite）的，进而可逆。岭回归的解存在且唯一。

Lasso的思想是在均方损失误差的基础上加上参数的 $l_{1}$ 范数作为惩罚项。新的损失函数是：

$L_{\lambda}(a_{0}, a_{1},..., a_{p}) + \frac{\lambda}{n}[|a_{0}| + |a_{1}| + ... + |a_{p}|]$

Lasso的求解相对于岭回归复杂一些，主流的算法是 Least Angle Regression(LARS).
Lasso倾向于得出稀疏（Sparse)解，岭回归倾向于得出稠密（Dense）解。

弹性网络（Elastic Net）结合了两者，同时使用 $l_{2}$ 范数和 $l_{1}$ 范数作为惩罚项，其形式如下：

$L_{\lambda}(a_{0}, a_{1}, ..., a_{p}) = L(a_{0}, a_{1}, ..., a_{p}) + \frac{\lambda}{n}(\tau \left \| \beta \right \|_{2}^{2} + (1 - \tau)\left \| \beta \right \|_{1})$

其中， $0 \leqslant \tau \leqslant 1$ 调节两种惩罚的比例，若 $\tau = 0$ ，则弹性网络回归化为Lasso回归；若 $\tau = 1$ ，则弹性网络回归化为岭回归。

弹性网络回归的好处是即保留了稀疏性，又可以把相关性高的变量同时找出来。

6. 均方误差的概率意义

线性回归采用最小化残差平方和主要有三个原因：第一，数学上残差平方和的解，在数据列满秩的前提下，存在且唯一；第二，平方和的解有显式数学解可以精确求得；第三，最小化残差平方和等价于正态（Gaussian）假设下的最大似然估计（Maximum Likelihood Estimation）。

对于第三点，假设数据来自 $y = X\beta + \varepsilon$ ,其中 $\varepsilon \sim N(0, \sigma^{2})$ 。

给定数据 $(X^{(1)}, y^{(1)}),.....,(X^{(n)}, y^{(n)})$ ,第 $i$ 组数据的似然即 $y^{(i)} - X^{(i)}\beta$ 在正态分布中的概率密度：

$L_{i} = \frac{1}{\sqrt{2\pi a}}exp[-\frac{(y^{(2)}-X^{(i)}\beta)^{2}}{2 \sigma ^{2}}]$

总体的似然为 $L = L_{1}L_{2}...L_{n}$ 。最大化似然即最大化每个数据的对数似然（Log Likelihood）之和：

$l = logL_{1} + ... + logL_{n}$

$logL_{i} = -log(\sqrt{2\pi} \sigma) - \frac{1}{2 \sigma^{2}}(y^{(i)} - X^{(i)}\beta)^{2}$

$l = -nlog(\sqrt{2 \pi}\sigma) - \frac{1}{2 \sigma^{2}}[(y^{(1)} - \widehat{y}^{(1)})^{2} + ... + (y^{(n)} - \widehat{y}^{(n)})^{2}]$

因此最大化 $l$ 等价最小化 $[(y^{(1)} - \widehat{y}^{(1)})^{2} + ... + (y^{(n)} - \widehat{y}^{(n)})^{2}]$ , 即残差平方和。

7. 岭回归的概率意义

岭回归从概率意义上可以看作在数据服从高斯噪声假设下，参数的先验分布（Prior Distribution）为以 0 为中心的正态分布。
若假设参数 $\beta$ 服从先验分布 $N(\overrightarrow{0}, \tau^{2} I_{p+1})$ ,则 $\beta$ 的先验概率为：

$prior(\beta) = Cexp-\frac{\left \| \beta \right \|_{2}^{2}}{2\tau^{2}}$

其中 $C$ 为只与 $p$ 和 $\tau$ 有关的常数。
根据贝叶斯定理（Bayes’ Theorem），数据的后验似然（Posterior Likelihood）与先验和 $L$ 的乘积成正比。

$posterior(\beta; X,y) \propto prior(\beta)L$

$log(posterior(\beta; X, y)) = C -\frac{1}{2\tau^{2}}\left\| \beta \right\|_{2}^{2} - \frac{1}{2\sigma^{2}}[(y^{(1)} - \widehat{y}^{(1)})^{2} + ... + (y^{(n)} - \widehat{y}^{(n)})^{2}]$

最大化后验似然等价于最小化：

$[(y^{(1)} - \widehat{y}^{(1)})^{2} + ... + (y^{(n)} - \widehat{y}^{(n)})^{2}] + \frac{\sigma^{2}}{\tau^{2}}\left\| \beta \right\|_{2}^{2}$

取 $\lambda = \frac{\sigma^{2}}{\tau^{2}}$ ，最大化后验似然等价于岭回归的损失函数。

类似地，Lasso 可以视作给参数一个拉普拉斯分布（Laplace Distribution）作为先验。

8. 常见的面试问题

Q:为什么需要正则化？

Q:为什么 $l_{1}$ 更容易给出稀疏解（Sparse Solution）？

Q: $R^{2}$ 是什么？应当如何计算？

Q:共线性应该如何检测？