一、最小二乘法：
1、矩阵、向量的求导法则：
思路：将前面的项看作一个整体，对后面求导后 再展开前面的 整体。
①行向量对元素进行求导：
②：列向量对元素进行求导：
③矩阵对元素进行求导：
④元素对行向量进行求导：
⑤元素对列、矩阵：类似上述方法。
⑥列向量对行向量求导、行向量对列向量求导：
⑦列向量对列向量求导：
注意：工程上用雅克比矩阵来计算列向量与列向量求导，即先将 第一个 列向量 转置转化为 行向量，然后求导。
⑧矩阵对矩阵的求导：将Y看做整体 求导后 展开。
2、向量导数性质公式：
- 向量的导数公式：
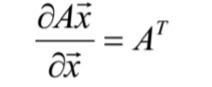
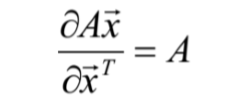
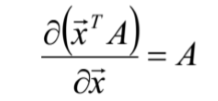
公式一 推导：
3、标量的导数公式：A 是一个 方阵。
注意：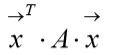 
是一个标量，其值为：二次型 f(x1，x2... xn) 的结果。
4、标量对方阵的导数：
5、最小二乘法：
作用：根据多组的实验数据，找出多个参数 a,b,c .. 与 真实结果的 近似函数关系。
方法：让多个参数a,b,c .. 同时满足 条件 实际上一般是不可能的，任何a，b代入上面各式都会发
生误差。于是想找a，b，c 使 上面各式的误差的平方和最小，误差的平方即二乘方，故称为最小二乘法。
过程：
①构造方程组：
②构造方程矩阵：A 是 系数矩阵 X 是参数 矩阵 B是真实值 矩阵。
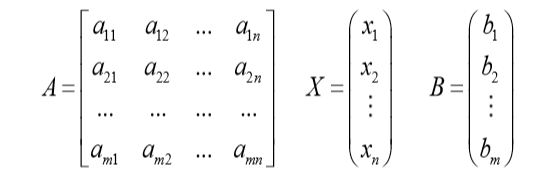
③ 将最小二乘结果转化为 列向量 AX - B 的 模的平方 ，求出函数的 最小值（极值，对 列向量 X 进行求导，）：
④ 结论：
例题：
例二：
二、特征值与特征向量：
- 理解：矩阵是一个向量组，由许多 行向量 和 纵向量 组成。
- 矩阵方程求解 用增广矩阵初等变换化为 E 。齐次/非齐次方程组 的解用 初等变化 化为 行最简阶梯型。
- 初步认为由多元一次方程组的系数组成（区别于矩阵初等变换求解矩阵方程）。矩阵是一种线性变换，可以将一些向量转化为另一种向量。
1、线性方程组求解：
①齐次方程组的解判定：
②非齐次方程组的解判定：
③基础解系与通解的概念：基础解系不是唯一的。
④实例： 求解线性方程组
- 注意：一定要将增广矩阵转化为 行最简阶梯型 。
2、特征值和特征向量：
①特征值特征向量的定义：
三：矩阵的分解：
1、海森矩阵：
是一个多元函数的二阶偏导数构成的方阵：
在具体点M0 的 海森矩阵：
①利用海森矩阵求解多元函数极值：
例题：
2、奇异矩阵（不可逆矩阵）：
3、正交矩阵与酉矩阵：
（1）正交向量的定义：
（2）正交矩阵与酉矩阵：它是方阵
正交矩阵与酉矩阵的两个特征：负数的正交矩阵叫酉矩阵
① 列(行)向量都是单位向量。 ② 两两正交。
（3）正交矩阵的性质：
4、QR分解：正交三角分解
前提：矩阵A必须满秩。
方法：QR分解 要求 矩阵A列向量的 正交矩阵Q 与 系数矩阵 R。
（1）QR分解的定义：
（2）施密特正交化过程 ：
（3）QR分解的步骤：
①写出矩阵A所有的列向量
②将列向量施密特正交化
③将上面矩阵单位化得到正交矩阵
④求出正交矩阵转化为矩阵A的系数矩阵R（上三角矩阵）。
例：
5、实对称矩阵的谱分解（SD）：
前提：矩阵 A 必须是 实对称矩阵。
方法：SD分解需要求矩阵A的 特征值 与 特征向量。
注意：SD分解时：特征值与特征向量的排序要一一对应。
（1）谱分解（SD）分解的定义：
（2）例题：
6、奇异值分解（SVD）分解：
前提：矩阵A没有特殊要求
方法：利用矩阵A的hermite矩阵 求出所有的特征值 与 特征向量 >>>>>>>> 求出 △ 和 酉矩阵 V ，由V1 求出 U1，在由 U1 扩充 出 U。
注意：特征值与特征向量的排序要一一对应；注意V1、U1 与 酉矩阵V 、酉矩阵 U的关系。
（1）SVD分解的定义：
（2）奇异值的定义：
奇异值的特点：必须从大到小排列，且全部大于零（hermite矩阵特征值排列后的平方根）
1、hermite 矩阵：
2、奇异值的定义：
（3）酉等价、酉相似：
（4）SVD分解的方法与步骤：
①求 矩阵A 的 hermite 矩阵的 酉相似对角矩阵 △ 及酉相似矩阵 V：
具体方法：1） 通过hermite矩阵 求出 所有的 特征值 和 特征向量
2）根据hermite特征值求出 矩阵A 的奇异值，再根据每个特征值 求出 对应的 特征向量，酉矩阵 V 就是
由 这些特征向量按照 奇异值的 排列顺序 的正交化矩阵。
3）将酉矩阵V 用 （V1, V2）来写：V1 是 奇异值或者特征值 > 0 对应的 特征向量，V2 是由剩余的特征向 量组成的。
②剩下的步骤：
例题：
