理论部分
1.方程形式
在进行数据处理过程中，有时数据图像可拟合成单变量线性函数，即
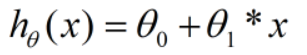
2.如何拟合
此时，我们虽知道拟合函数的形式，但如何拟合仍是个问题，怎样拟合可以最接近实际数据情况呢？
最小二乘法
此时我们引入代价函数这个概念
-
代价函数
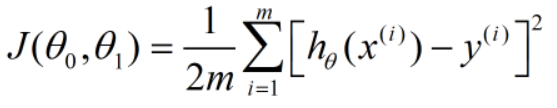
接下来我们来分析如何引入这个式子
首先先看求和符号右边的平方式，这个平方式也叫做平方损失函数，这个式子是怎么来的呢？
对于一个拟合的线性函数，函数对应的直线上的点到数据点的距离的平方为
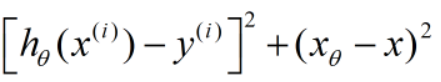
因为此模型为监督学习模型，每个x对应的y值都已给出，所以存在：
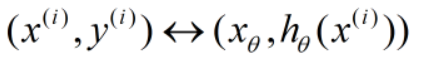
两个x相等，不同的只是对应的实际值y和预测值h（x）,所以此式后半部分为0.
那么，对于一个图像的拟合程度如何描述，只需要在有限的训练数据集中，对所有的点和预测方程直线的点之间的距离的平方（差距扩大化）进行求和。
左侧的1/2m的作用：
1/m是为了得出平均差距；
1/2是在后来求偏导的过程中抵消平方对应的2，而不对损失函数本身造成影响。
3.问题解决目标
我们已经知道了我们预测的线性方程对数据集的拟合程度的标准为代价函数
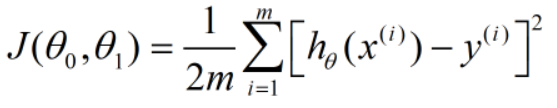
那么，接下来我们对此问题的处理便变成了一个对代价函数的最小化处理问题，即
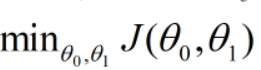
不过，在进行对代价函数最小化问题的处理之前，我们先来看看代价函数的工作原理。
4.代价函数的工作原理
吴恩达老师对代价函数的工作原理的分析由浅入深
因为此编辑器不支持对特殊数学符号进行处理，所以，我们暂且对h(x)换一种表述方法
-
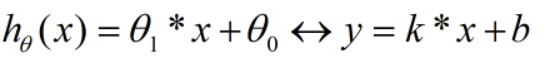
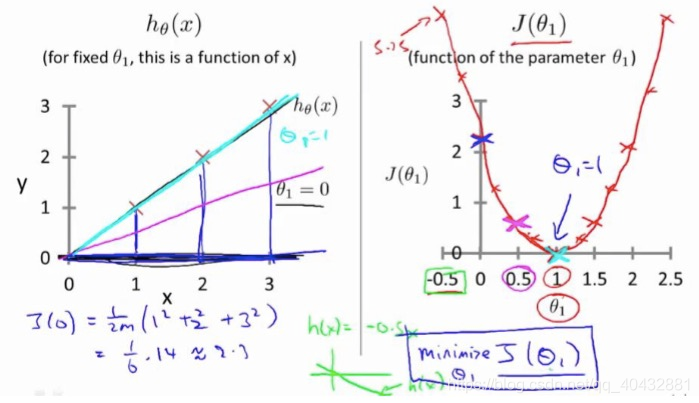
当b=0时
此时的拟合直线必为一个过原点的直线，当达到最佳拟合位置时，
此时的代价函数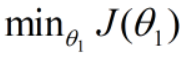
最小，此时的x对应的x0，随着x值向x0两侧远离，对应的代价函数的值也在增大,此时的代价函数大致是一个如图所示的抛物线：
当b不等于0时
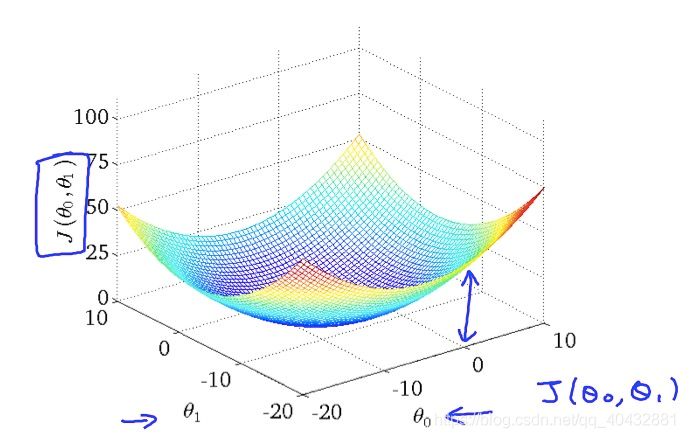
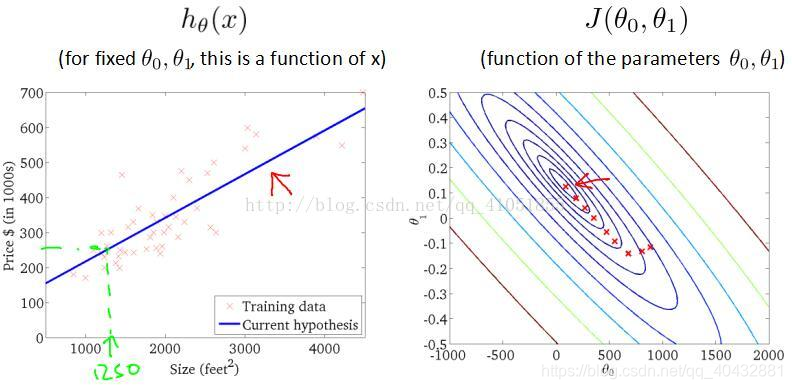
此时，影响代价函数的因素便变成了两个（k和b），因为b和k的效果一致，所以当k=0时，b对应的代价函数也大致是一个抛物线，当二者均不为0时，其对应的代价函数便是一个三维凸面：
其在下方平面上的投影为下图右侧的轮廓图：
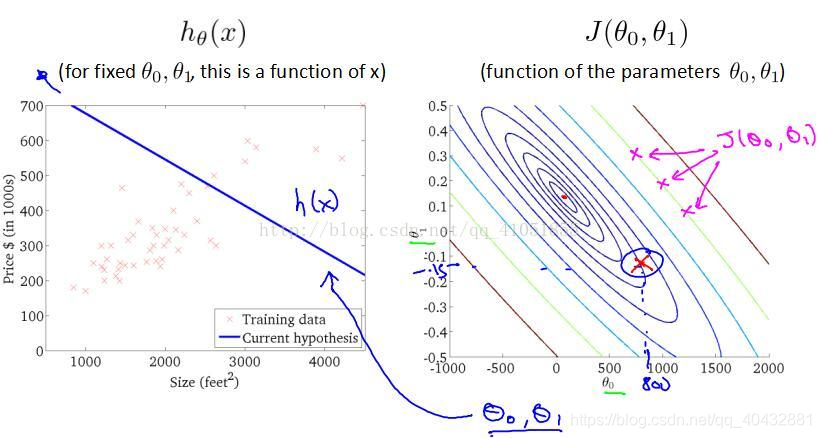
图上相同直线上的点对应的代价函数是等值的，代价函数的最小处为图上的中心点。
此时，我们已经了解了单变量线性回归模型的本质所在：对三维凸函数的最小点求解。下面我们来引入处理此问题的算法：梯度下降法。
5.梯度下降算法
梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数的最小值。
梯度下降的思想：开始时随机选择某一个具体的θ0和θ1，计算代价函数，然后寻找下一个能让代价函数值下降最多的参数组合。持续这么做，直到到一个局部最小值。选择不同的初始参数组合，可能会有不同的局部最小值，所以在没有尝试完所有的参数组合，不能确定得到的局部最小值是否是全局最小值。
如下图所示，从某一点开始，每次沿着一定的梯度下降直到达到一个极小值为止。梯度下降和下山一样，坡度不一样，下降的速度就不一样，而且有可能走向不同的最低点。下降梯度算法可以帮助我们改变θ0，θ1的值。（α称为学习率，后面的偏导是梯度）
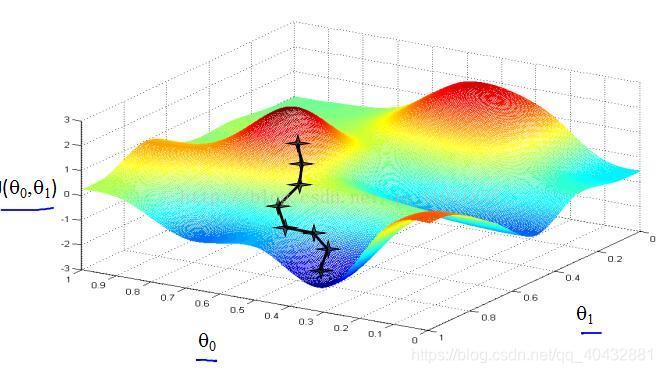
要注意两个参数应同时更改（对应的代价函数值不变），右边错误的原因在于先改变θ0的值，对应的代价函数的值也会改变。
梯度下降算法得到的是局部最小值，并非全局最小值，而对于单变量线性回归模型来说，其代价函数对应的是一个凸函数，最后获得的局部最小值便是全局最小值。
下面我们来解释一下上面参数更改式子的由来：
-
微分部分（梯度）：
令θ0=0，假设θ1在最低点的右侧，此时梯度是正数，根据梯度下降算法更新θ1，它的值会不断减小，靠近最低点。
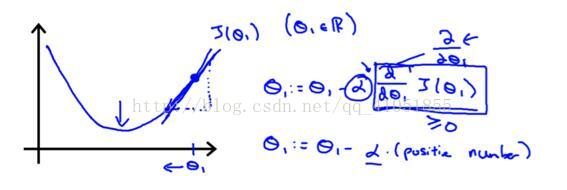
同理假设θ1在最低点的左侧，此时梯度是一个负数，根据算法更新θ1，值会增大，靠近最低点。
所以微分部分达到了下降的目的。 -
学习速率α：
通俗来说，如果将凸函数看做是山峰，待处理的问题是如何下到山底，此时，微分部分梯度下降已经保证了我们会一直下山，α的作用便在于控制了我们下山的步子大小。α大，下山快；α小，下山慢。
这样看来，α不应该越大越好吗？
事实并非如此，我们除了要考虑训练时间外，还应考虑精度的问题：
学习率α也会影响梯度的下降。α太小，θ的变化会很小，梯度下降会很慢。相反，α太大，θ的变化会很大，可能越过最低点，可能永远没法达到最低点。
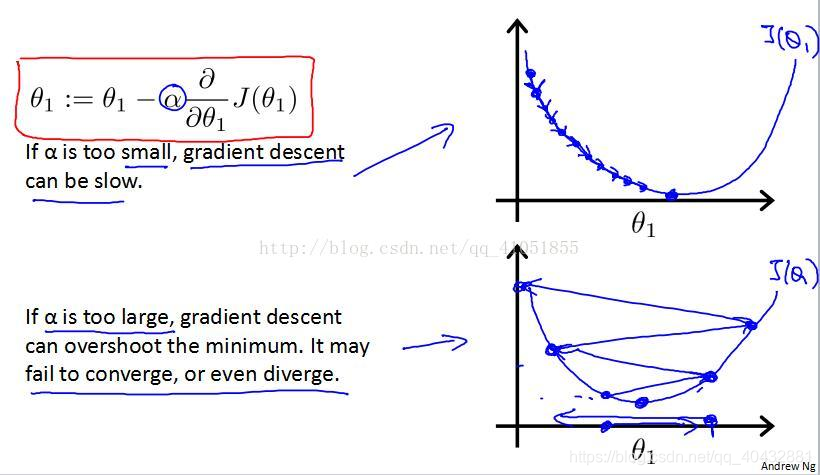
梯度下降法同时改变了函数的两个参数，那么，学习速率α是否也应随之改变呢？
其实并不需要。下面我们来看一下梯度下降的过程：
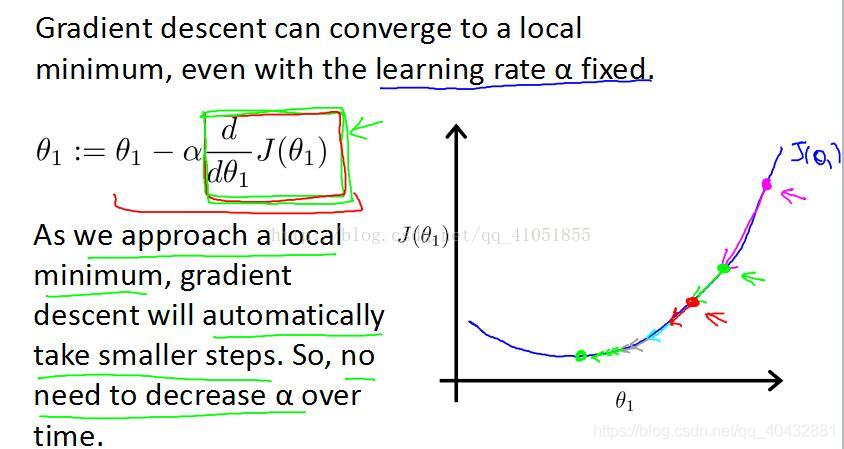
对最低点越来越接近，那么斜率会逐渐减小，每次下降程度会越来越小，所以不需要改变α的值来减小下降程度。
接下来的问题便是对于微分项的处理了。 -
微分项处理：
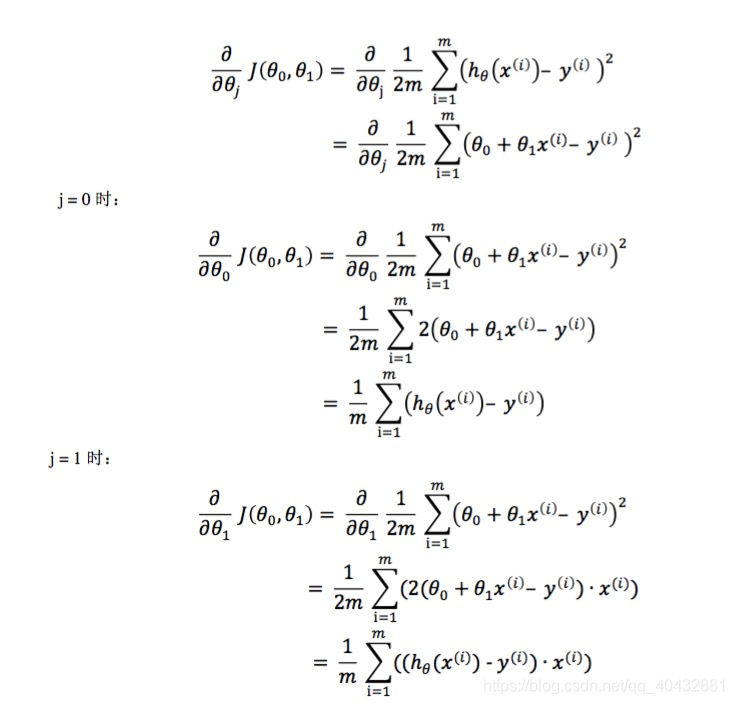
6.梯度下降算法的迭代过程
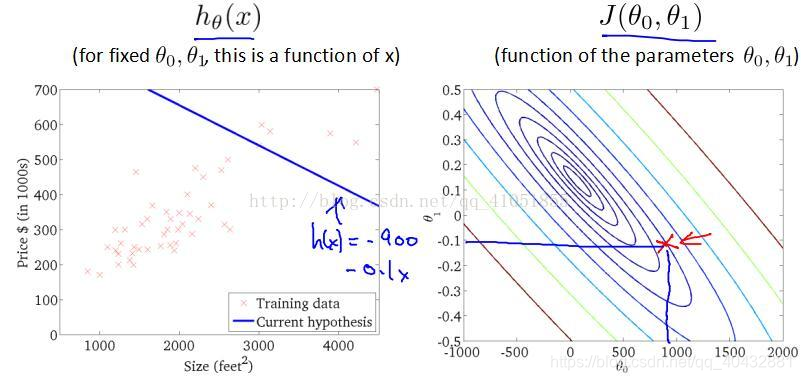
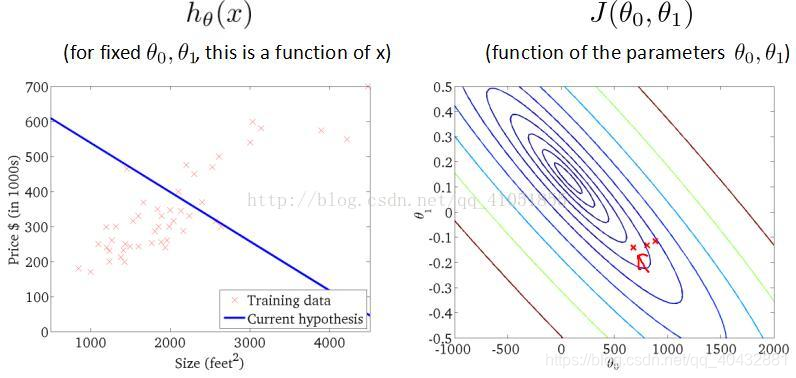
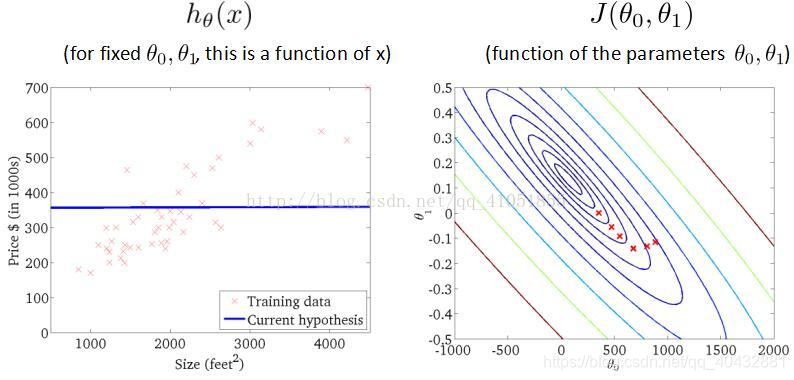
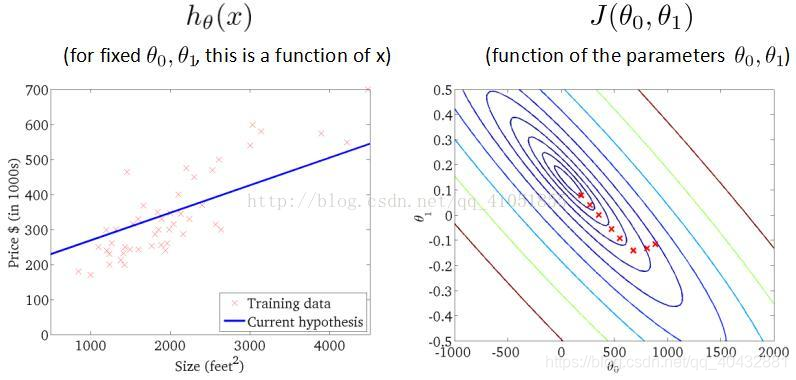
以上便是单变量线性回归模型的理论部分的解释。