降维（一）PCA (李宏毅机器学习）

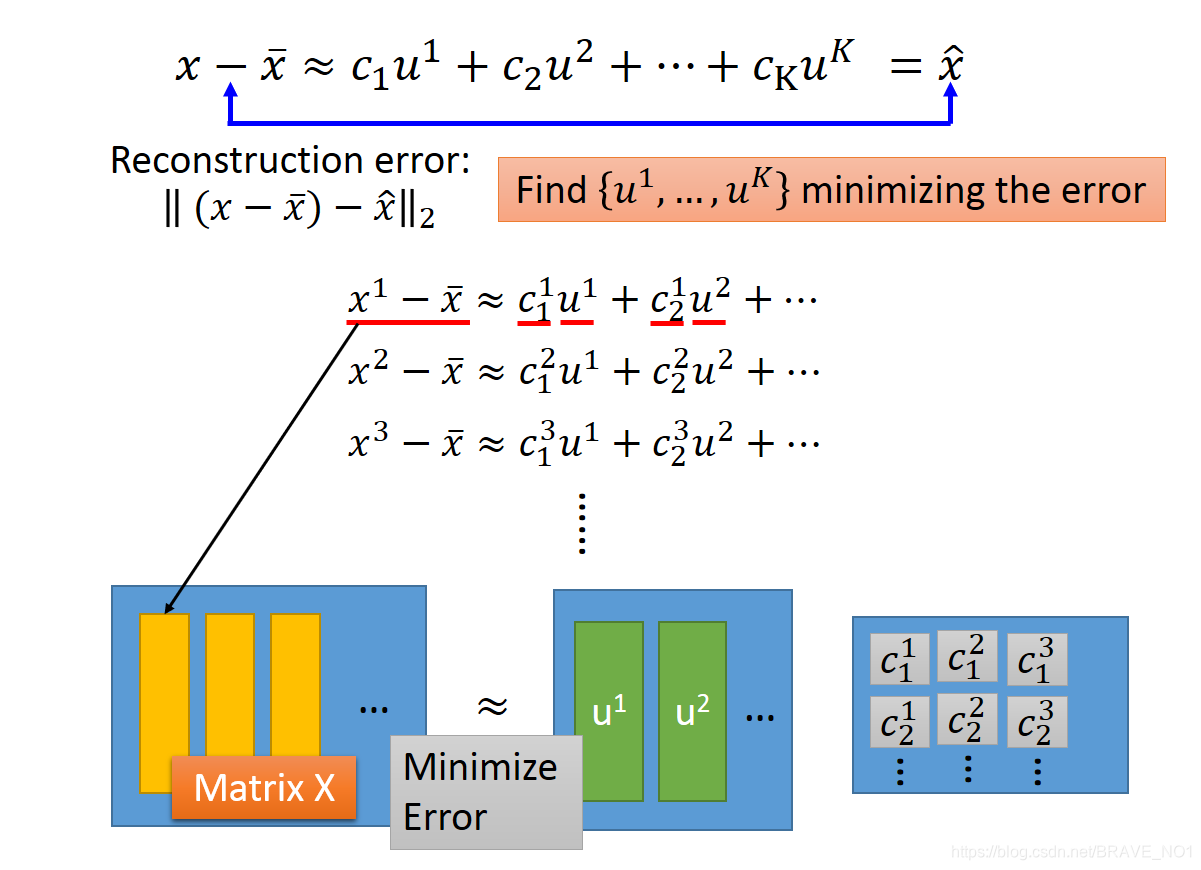
一直以来数据降维是非常重要的预处理步骤，通过数据降维，我们可以实现数据可视化、数据降噪、数据压缩等目标。那么如何定义降维呢？我们定义一个映射矩阵W，z=w*x，则表示原数据通过矩阵W变成Z。

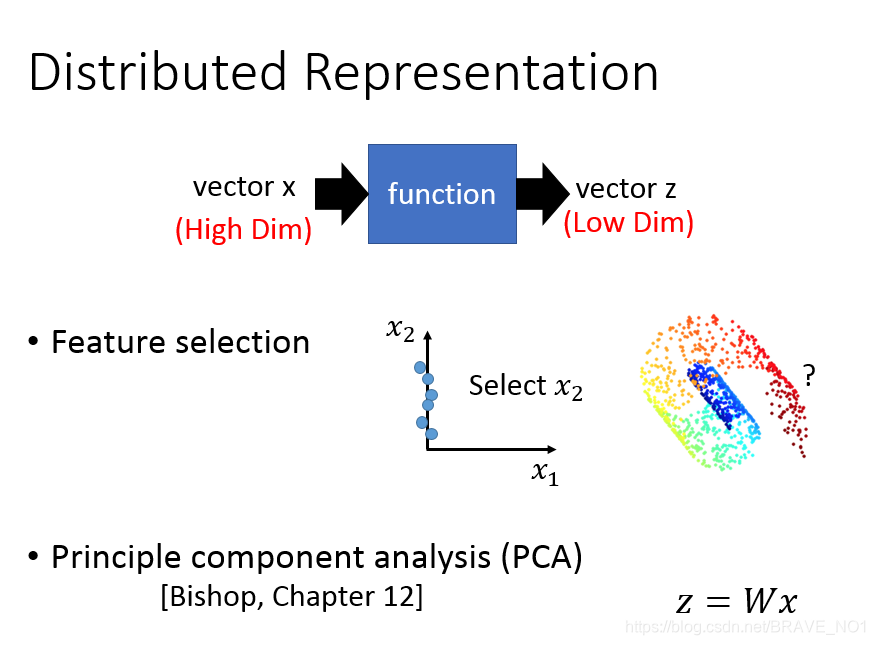
PCA（principle component analysis主成分分析）

主成分分析总体来说是为了在降维的过程中尽可能的保存信息。那么如何衡量信息呢，我们考虑到了熵： $-\int p lnp$。熵中用到了概率分布，那么如何求解pdf(概率密度函数），我们考虑到了高斯。那么如何度量保存了信息的大小呢，我们考虑到了方差。如果原数据X与降维后的数据Z之间的方差接近，那么我们认为保存了足够的信息。但是var(Z)与var(X)是不同维度的数据，无法比较，所以我们可以换个角度进行思考。因为X是已知的，则var(X)也就是已知的。而var(Z)越大也就是离var(X）越近，最大也不会超过var(X)。这样一来，我们的目标就变成了使得Var(Z)最大化。

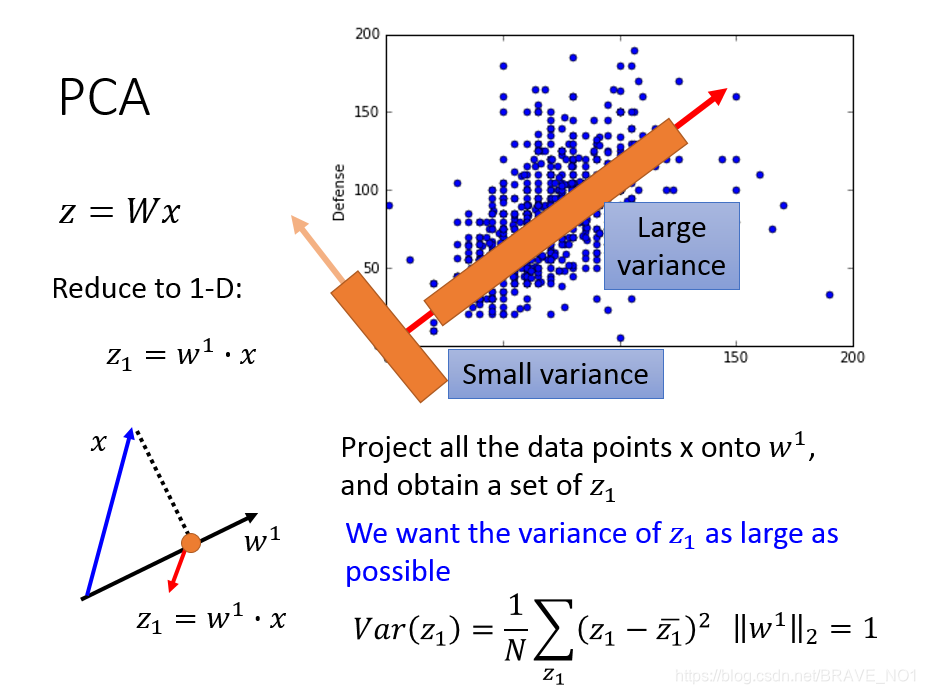
在图中，当投影在方差大的方向时，保存得信息最多。

那我们就开始计算：从第一个主成分开始： $z_1=w^1x$：

根据前面对W的声明，它是一个正交矩阵，那么我们在这里可以添加约束认为是标准正交矩阵。那么可以添加约束 $(w^1)^Tw^1$=1。因此我们可以采用拉格朗日办法求解最大值问题：

根据推导我们发现使得方差最大化，最后竟然变成了使得特征值最大，那么也就是说当我们选取最大的特征值时，方差最大，而 $w^1$则刚好就是协方差矩阵S的最大的特征值对应的特征向量。这里还有一点数学知识需要明确：由于S是半正定的实对称矩阵，所以他的特征向量正交。
下面我们求解第二个主成分： $z^2=w^2x$(求解过程与1非常类似）

由于 $(w^1)^Tw^2$=0, $(w^1)^Tw^1$=1, $(w^1)^TSw^2$= $(Sw^1)^Tw^2$= $\lambda_1(w^1)^Tw^2$=0,因此从上图可以推导出 $\beta$=0。因此我们可以推出：

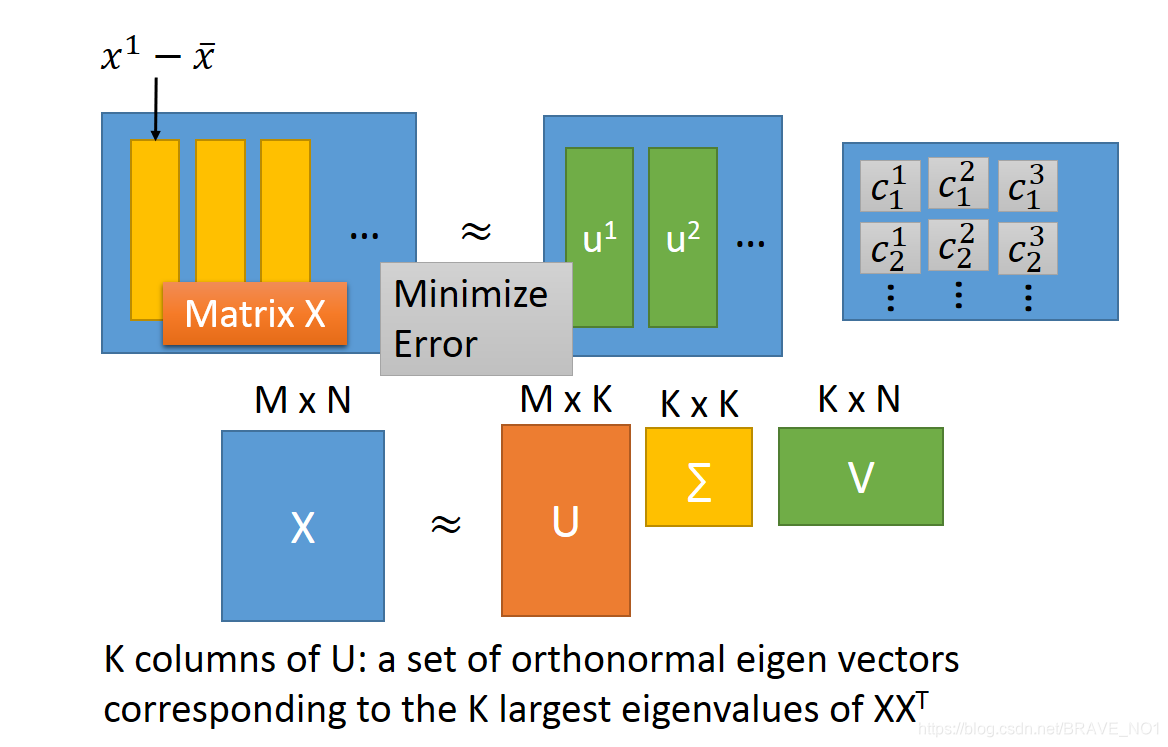
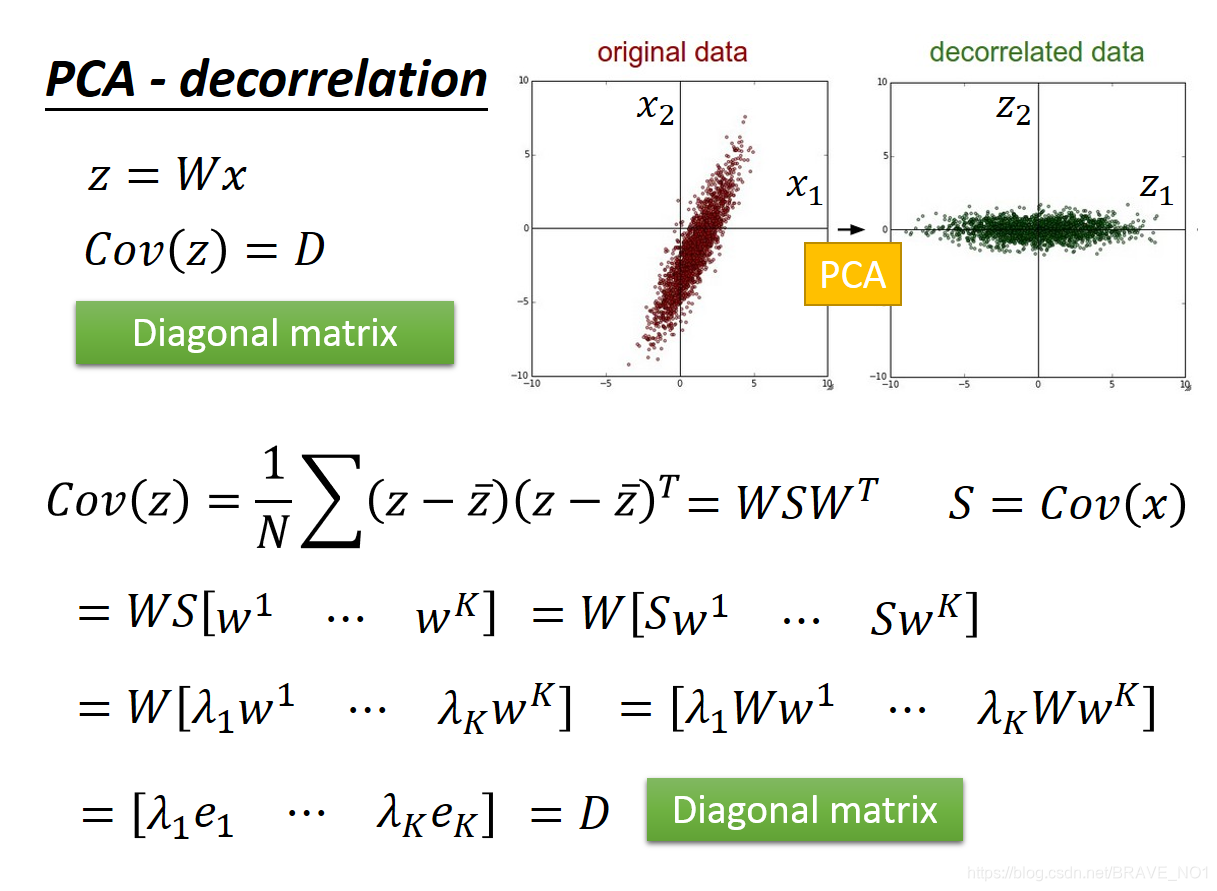由此我们可以推论：整个过程其实就是一个使协方差矩阵对角化的过程。协方差矩阵主对角线是方差，其余元素是协方差，所以整个过程就是一个使得协方差不断变小趋于0的过程。而我们的目标也就是求解使得协方差矩阵S对角化的矩阵W，也就是我们的投影矩阵。看到这个形式，是不是想到了奇异值分解。所以奇异值分解也也是PCA的一种求解方法。从重建的角度来分析这个问题。

x-mean(x）表示降维前的数据。而（ $\acute{x}$）表示降维后的数据，用主成分组成。当二者之前的Loss越小，我们则认为保存的信息越多，降维效果越好。