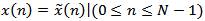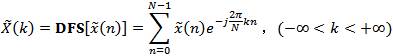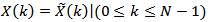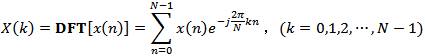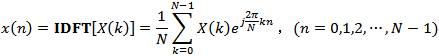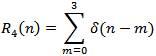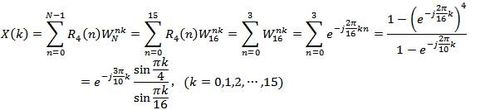1.闲话放在前面扯
什么是频域?从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。所以我们眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
2.严密的数学推导
我们知道,在离散傅里叶级数(DFS)中,离散时间周期序列在时域是离散的n ,其频谱是离散频率周期序列,在频域也是离散的k,理论上解决了时域离散和频域离散的对应关系问题。但由于其在时域和频域都是周期序列,所以都是无限长序列。无限长序列在计算机运算仍然是无法实现。为此必须取有限长序列来建立其时域离散和频域离散的对应关系。
DFS的主值序列:我们知道,离散时间周期序列 是一个无限长序列,其傅立叶级数展开式为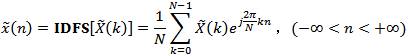
可以看出时间点序号n 是以N为周期的,如果只取其一个周期,称之为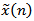
主值序列x(n)就是一个长度为N的有限长离散时间序列。同理,的DFS也是一个无限长序列,即傅立叶系数:
也可以看出频率点序号k 也是以N为周期的,如果只取其一个周期,称之为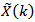
主值序列X(k)是一个长度为N的有限长离散频率序列。可见,离散时间周期序列在时域和频域的主值序列,均为有限长离散序列。且主值序列的长度均为N(即n,k=0,1,2,…,N-1)。
离散傅里叶变换:
在离散傅立叶级数(DFS)中,取其时域和频域的主值序列,变换仍然成立。这就是离散傅里叶变换(DFT),即:
和其逆变换(IDFT):
可见离散傅里叶变换(DFT)只不过是特殊的离散傅立叶级数(DFS),就是对其时域和频域都仅取主值序列。
离散傅立叶级数(DFS)中的无限长序列
和
都是以N为周期的周期序列,所以在计算离散时间周期序列及其频谱时,可以利用DFS的周期性,只需要在时域和频域各取一个主值序列,用计算机各计算一个周期中的N个样值,最后将所得的主值序列x(n)和X(k)进行周期延拓,即可得到原来的无限长序列
和
。
由DFT的导入过程可以发现,DFT不仅可以解决无限长周期序列的计算机运算问题,而且更可以解决有限长序列的计算机运算问题。事实上,对于有限长离散序列,总可以把时域和频域的变换区间(序列长度)均取为N(包括适当数量的补0点),通常把N称之为等间隔采样点数,我们可以把这个N点的变换区间视为某个周期序列的一个主值序列,直接利用DFT的定义计算其N点变换。
3.代表性的实例
1.单纯的从计算角度出发。假设有一个序列长度N=4,具体的x(n)={1,2,-1,3},n=0,1,2,3。
首先,由N=4得到 :
于是有:
反变换:
2.补零,增加有限长序列的长度是否能够提高物理分辨率?
有效长度N 1 =4的单位矩形序列:
如下图所示:
如果变换区间等间隔采样点数N=16(注意:可以补零延伸为序列有效长度N 1 的整数倍),则其16点的DFT频谱为
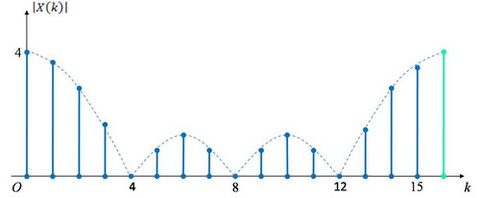
其16点DFT的幅度频谱图如下:
当然,如果取变换区间N=32,即在有限长离散时间序列尾部补零更多位,则32点的DFT谱线更密。这是因为增长观察时间,可提高频率分辨率。但DFT频谱的包络,始终与非周期序列的离散时间傅立叶变换DTFT的连续频谱曲线一致。这又表明DFT是DTFT连续频谱的离散化。