12.离散傅里叶变换（DFT） [学习笔记]

不同于网上的直接推导离散傅里叶变换的方法，本文将从连续傅里叶出发，用采样近似的方法来推导出离散傅里叶变换

推导的思路是：

1. 先对连续函数$f$进行离散化操作，即采样，得到离散的点$f_{sampled}$。
2. 然后对其傅里叶变换${\scr F}(f_{sampled})$进行采样，得到$({\scr F}(f_{sampled}))_{sampled}$
3. 最后，再将连续傅里叶变换本身${\scr F}$也转换为对应的离散形式${\scr F}_{sampled}$

总的来说，离散傅里叶变换（DFT）就是用离散的点来近似得到$f$，${\scr F}f$以及${\scr F}$

---

第一步

首先需要说明的一点是：在连续傅里叶变换中，一个信号不能同时在时域、频域都受到限制。
举一个简单的例子，如果时域中的信号是矩形函数，即被限制在某一范围内，其他点的值均为$0$，那么它的傅里叶变换就是$sinc$函数，即在频域中是不受限的。反之亦然。

但是作为离散傅里叶变换，我们希望探究的问题无论在频域还是在时域内都是有限的（根据采样而定）。为了导出有限值，我们不妨先假定研究的函数在时域、频域内都受限。

设$f(t)$在时域内受限，$0 \leq t \leq L$
对应的${\scr F}f (s)$在频域内受限，$0 \leq s \leq 2B$，其中$B$为带宽（注意为了方便计算，我们将区间从$-B \leq s \leq B$平移了）

根据上一章的内容可知，以两倍带宽作为采样频率可以保留完整的信息，因此我们不妨把采样频率设为$2B$，相当于我们在时域上每隔$\frac{1}{2B}$的距离取一个点，如下图

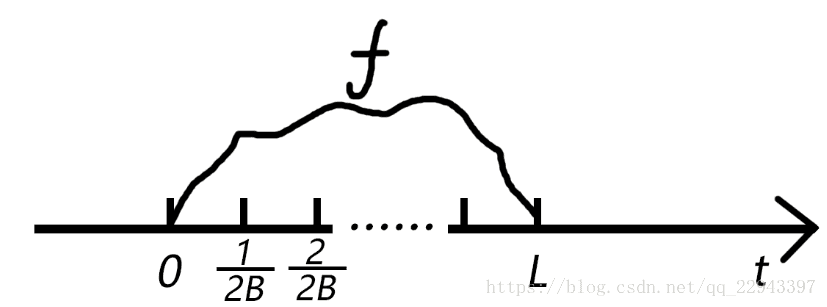
于是，在时域中的采样点个数就是$N = \frac{L}{\frac{1}{2B}}=2BL$，每个采样点在时域中的横坐标就应为：$t_0 = 0, t_1 = \frac{1}{2B}, \dots , t_{N-1} = \frac{N-1}{2B}$，对$f(t)$进行采样，采样位置为$t_0, t_1, \dots, t_{N-1}$，可以得到$f_{sampled}(t)$：

$$\begin{align*} f_{sampled}(t) &= f(t)\delta(t-t_0) + f(t)\delta(t-t_1) + \dots + f(t)\delta(t-t_{N-1})\\ &=\sum_{k=0}^{N-1}f(t)\delta(t-t_k)\\ &=\sum_{k=0}^{N-1}f(t_k)\delta(t-t_k)\tag1 \end{align*}$$

---

第二步

对$(1)$式进行连续傅里叶变换，注意$(1)$式中变量是$(t)$，故$f(t_k)$实际上是一个常量

$$\begin{align*} {\scr F}f_{sampled} (s) &= \sum_{k=0}^{N-1}f(t_k) {\scr F} \left(\delta(t-t_k) \right)\\ &=\sum_{k=0}^{N-1} f(t_k) e^{-2\pi ist_k} \end{align*}$$

用与第一步类似的方法，与$2B$类似，我们将$L$定为在时间上的一个限制，于是，根据频率与时间的倒数关系，我们可以在频域内对函数进行采样，采样间隔为$\frac{1}{L}$。如下图：

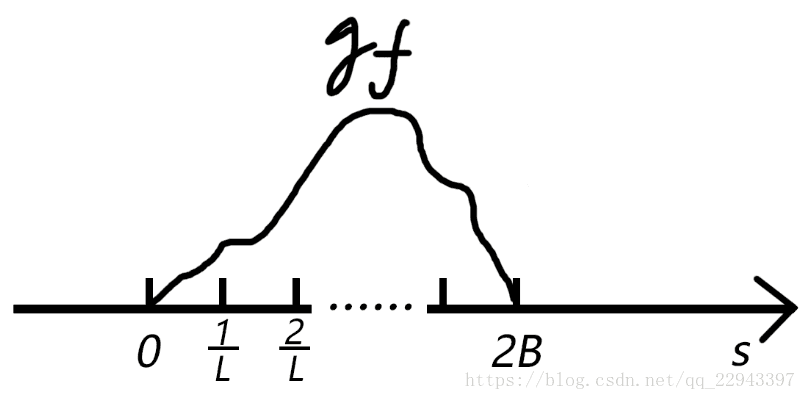
于是，在频域中的采样点个数就是$M = \frac{2B}{\frac{1}{L}}=2BL$，我们发现$M=N$，因此，每个采样点在频域中的横坐标就应为：$s_0 = 0, s_1 = \frac{1}{L}, \dots , s_{N-1} = \frac{N-1}{L}$，对${\scr F}f(s)$进行采样，采样位置为$s_0, s_1, \dots, s_{N-1}$，可以得到$({\scr F}f_{sampled})_{sampled}(s)$：

$$\begin{align*} ({\scr F}f_{sampled})_{sampled}(s) &= \sum_{k=0}^{N-1} f(t_k) e^{-2\pi ist_k} \sum_{m=0}^{N-1} \delta(s-s_m)\\ & = \sum_{m=0}^{N-1} \sum_{k=0}^{N-1} f(t_k) e^{-2\pi is_m t_k} \delta(s-s_m) \end{align*}$$

清楚起见，我们将上式左边部分记为$F(s)$，则

$$F(s_m) = \sum_{k=0}^{N-1} f(t_k) e^{-2\pi is_mt_k}\tag2$$

---

到此为止，我们已经在某种程度上得到了DFT，但是$t_k$和$s_m$其实是连续图像中截取的点，因此为了彻底消除连续性，我们进行以下操作：

根据前文采样时下的定义，可知$t_k = \frac{k}{2B}$，$s_m = \frac{m}{L}$，于是我们就可以将$(2)$式改写为

$$\begin{align*} F(s_m) &= \sum_{k=0}^{N-1} f(t_k) e^{-2\pi is_mt_k}\\ &=\sum_{k=0}^{N-1} f(t_k) e^{-2\pi i\frac{mk}{2BL}}\\ &=\sum_{k=0}^{N-1} f(t_k) e^{-2\pi i\frac{mk}{N}} \end{align*}$$

至此，所有连续性消除，而上式括号中的原变量$t_k$，$s_m$其实也已经变成了变量$k$，$m$

---

最后，我们写出DFT的完整表达：

为了区别于连续值，我们以下划线的形式记录离散值

假设$\underline{f}$为一组离散的信号：

$$\underline{f} = \left( \underline{f}[0], \underline{f}[1], \dots, \underline{f}[N-1] \right)$$

则该信号经DFT后：

$$\underline{F} = \left( \underline{F}[0], \underline{F}[1], \dots, \underline{F}[N-1] \right)$$

其中，DFT的表达式为：

$$\underline{F}[m] = \sum_{k=0}^{N-1} \underline{f}[k]e^{-2\pi i\frac{mk}{N}}$$

---

注意到在推导过程中，$\Delta t = \frac{L}{N}$，$\Delta s = \frac{2B}{N}$，故$\Delta t \Delta s= \frac{2BL}{N^2} = \frac{1}{N}$，这说明了$\Delta t$与$\Delta s$存在着倒数关系，且在我们设置采样参数时，只要确定了$\Delta t, \Delta s, N$中两个，另一个就被确定了。

同时我们发现时域、频域的间隔关系中有一个系数$N$，这个系数在下一章会出现在离散傅里叶逆变换中