【Opencv】离散傅里叶变换DFT

离散傅里叶变换DFT

声明：这篇文章的图片大多是从其他网站获取的，图片来源见参考文献。如果文本有哪里理解的不对，还望指正。

1. 离散傅里叶变换

1.1 离散傅里叶变换与傅里叶变换

傅里叶变换对于信号分析来说是一大利器，他把信号从时域转换到了频域，使得我们能够更加直观的看出信号所包含的信息。傅里叶变换的理论来源在于，任何一个函数都可以表示为无数正弦波的叠加。我们对一个信号做傅里叶变换，实质上是为了获得信号的三个信息：信号的频率组成、分量的幅度和相位信息。

但是傅里叶变换只能处理连续的信号，而计算机是没有办法处理连续信号的，所以，通过对信号抽样的方式，就有了离散的傅里叶变换，这样就可以被计算机处理了。傅里叶变换到离散傅里叶变换的过程如下：

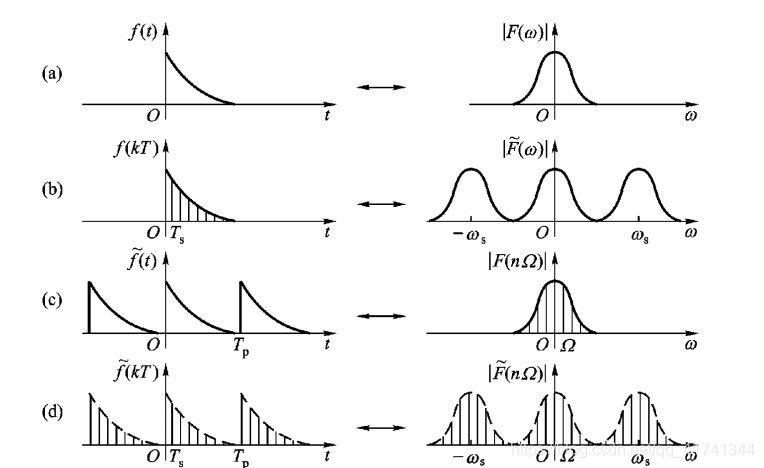
图（a）任意信号f(t)及其傅里叶变换之后的频谱图
图（b）是对连续信号f（t）进行抽样之后得到的频谱图
图（c）根据傅里叶变换的对称性，时域为周期函数时，频域必定为抽样函数
图（d）对时域和频域同时抽样，就同时得到了离散的信号及其频谱。注意，离散傅里叶变换的两端均为周期函数，我们一般使用的都是他的主值区间。

1.2 离散傅里叶变换之后得到了什么

像傅里叶变换那样，F(ω)代表的是对信号进行分解，频率为ω的正弦分量的幅度和相位
$F(\omega)=\int_{-\infty}^{\infty} f(t) \cdot e^{-i \omega t} d t$
离散傅里叶变换的公式是这样的：
$正变换：X_{k}=\sum_{n=0}^{N-1} x_{n} \cdot e^{-i 2 \pi k n / N}$
$逆变换：x_{n}=\frac{1}{N} \sum_{k=0}^{N-1} X_{k} e^{i 2 \pi k n / N}$
我们从正变换中可以看出，离散傅里叶变换的2πk/N与傅里叶变换中的ω相对应。
故离散傅里叶变换之后的频域上的复数X_k（假设为a+bj)，实际上就代表了频率为2πk/N的正弦分量的幅度和相位特性。

而其反变换意义就是，各个信号分量通过怎么样的权重叠加能够得到原来的信号，这个权重就是离散傅里叶变换的结果X_k

1.3 离散傅里叶变换的共轭性

离散信号经过离散傅里叶变换之后得到的N个点，事实上，只有N/2个点的数据是有效的，我们可以通过下面的式子看出，X[N-k]与X[k]是共轭的，他们的幅值相等，相位相反。因此，离散信号经过离散傅里叶变换之后，得到的幅度图是对称的。不过，对于离散信号分析，得到的那个共轭点的信息是无效的。通过抽样定量可知，对时域信号与f_s的频率进行抽样，频域上不失真的信号频率最大为f_s/2。所以，与低频信号共轭的那个信号点的信息是无效的。
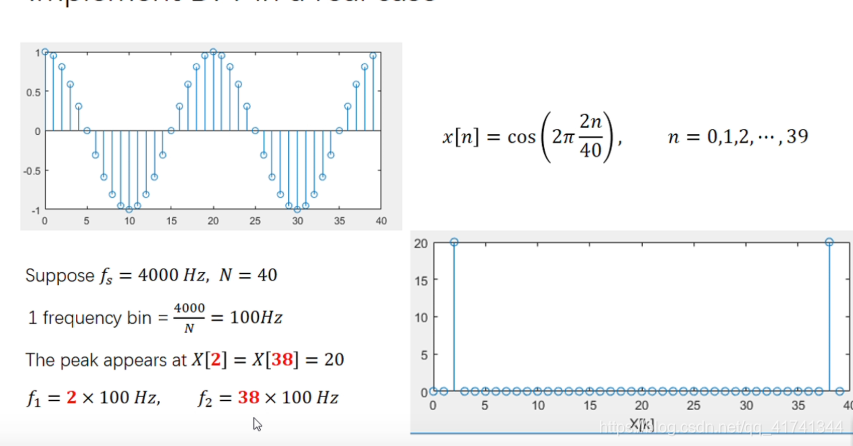
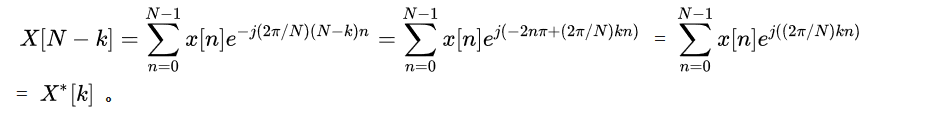比如对下面这张图进行离散傅里叶变换分析，得到的频谱图有两个峰，说明信号频率可能是200Hz,也有可能是3800Hz，但是由于高频信号点是失真的，所以，表示的信号应该是200Hz的正弦信号

2. 二维离散傅里叶变换

2.1 二维离散傅里叶变换的实质

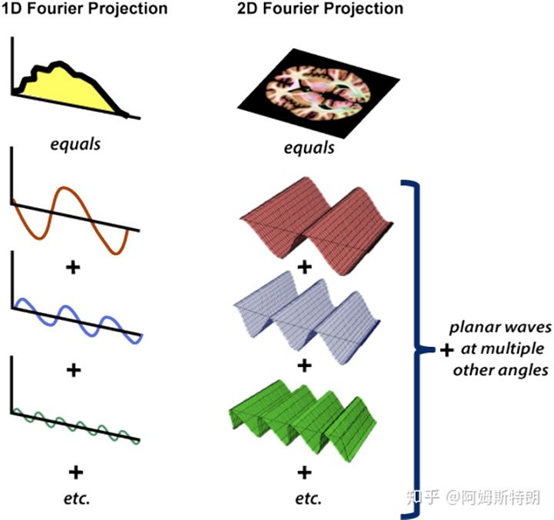
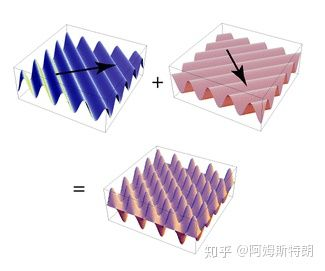
一维傅里叶变换表示的是信号能够由一个个的正弦分量叠加而成，而二维傅里叶变换的实质在于，所有的二维信号，都能够被分解为正弦波平面。正弦波平面可以看做是一个正弦波，沿着法方向拉伸得到的。

图片分解为正弦波平面的叠加

正弦波平面的叠加

对于一维的傅里叶变换，我们知道，要是想表示一个信号，就需要知道正弦分量的频率、幅度和相位。相类比，如果我们想表示一个二维的信号（比如图片信号），我们想要用正弦波平面来表示，除了需要知道这个正弦波的频率、相位、幅度之外，还要知道这个正弦波平面的延展方向。
$\begin{aligned} F(k, l)=& \sum_{i=0}^{N-1} \sum_{j=0}^{N-1} f(i, j) e^{-i 2 \pi\left(\frac{k i}{N}+\frac{1 i}{N}\right)} \\ & e^{i x}=\cos x+i \sin x \end{aligned}$

2.2 二维离散傅里叶变换储存的复数的含义

参考一维离散傅里叶变换，我们知道，X[k]中储存的复数为频率为2πk/N的正弦量的幅度和相位信息。那么对于二维傅里叶变换来说，F（k，l）中储存的复数就是，以cos（2πk/N）*cos（2πl/N）为基准的正弦波平面的幅度和相位。而二维点（k，l）表示的就是正弦波平面的拉伸方向。

不过，往往我们对一张图片做二维的离散傅里叶变换，是以左上角的那个点为原点的，因此，左上角的正弦波平面是低频信号，所以幅度会比较大，再加上离散傅里叶变换的共轭性（可以看下文2.4部分体会一下这个共轭性），四角的幅值都是相同的，所以一张图片的离散傅里叶变换结果，往往是四角亮（低频信号区幅值大，对应的灰度图就是偏白色），中间黑（高频信号区幅值小，对应的灰度图就是偏黑色）

为了看频谱图方便，人们往往会把原点移动到图片的中心，这样看起来会方便很多，原点移到中心以后，含义就变成了中心是低频正弦波平面区域，四角为高频正弦波平面区域，效果如下：

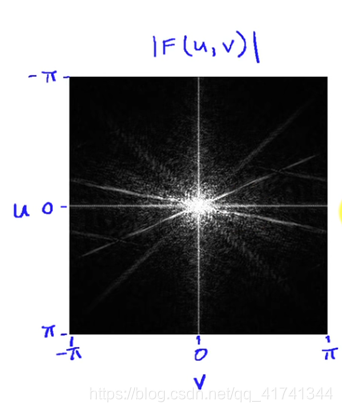
2.3 二维DFT的直观表示

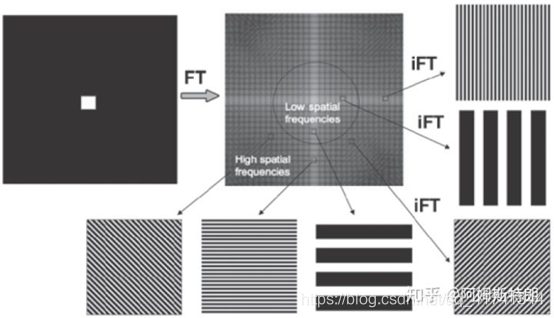
也就是说，我们经过2D DFT之后得到的矩阵集合点，实际上就代表了一张张正弦波平面分量的幅度和相位特性。比如下面这张幅度图的正弦波平面分解示意图。原点在中心，越靠近中心的正弦波平面条带（可以看做是俯视图）越少，因为靠近原点的正弦波平面频率低，所以振动次数少，而远离中心点表示的正弦波平面条带次数就多，因为正弦波平面的频率高。沿对角线方向的正弦波平面呈现45度的斜线样子，因为表示方向的坐标（k，i）两个数字是一样的，合成的角度就是45度。

经过离散傅里叶变换的矩阵，就是表示这些正弦波平面的幅值和相位。

2.4 二维傅里叶变换的过程

二维傅里叶变换公式如下：
$\begin{aligned} F(k, l)=& \sum_{i=0}^{N-1} \sum_{j=0}^{N-1} f(i, j) e^{-i 2 \pi\left(\frac{k i}{N}+\frac{1 i}{N}\right)} \\ & e^{i x}=\cos x+i \sin x \end{aligned}$
2D DFT其实就是分别在两个维度上做了DFT，具体过程如下：
（1）原始图片

（2）先对垂直方向做一次一维离散傅里叶变换

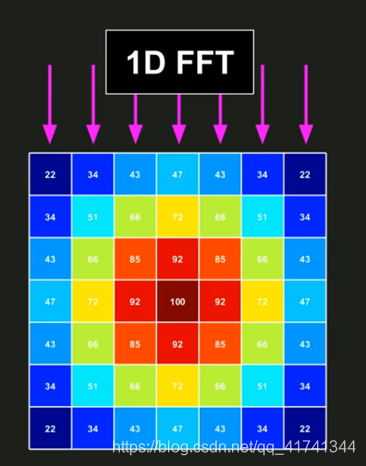
（3）得到如下结果

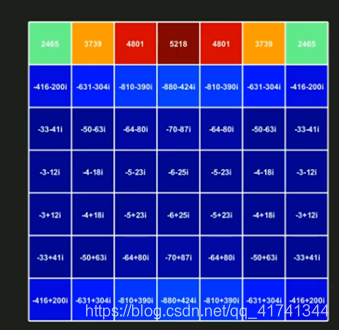
我们能够看到，在竖直方向做傅里叶变换仍然具有共轭特性，与水平中心线对称的两个点，实部不变，虚部对称。
（4）对水平方向做一次1D DFT

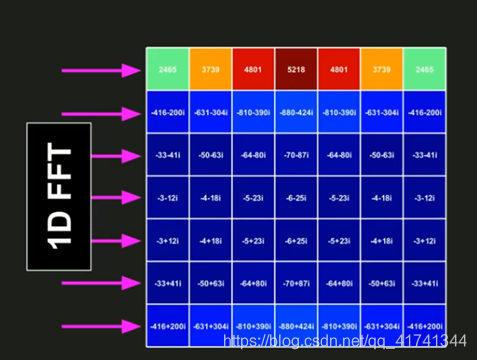
（5）2D DFT的结果

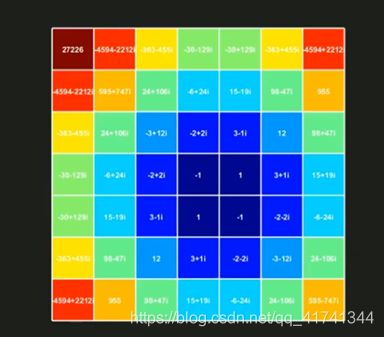
这样我们就得到了最终的一个二维的傅里叶变换矩阵。这个矩阵水平方向和竖直方向均具有共轭特性，如果把矩阵内的复数全部取根下平方和（也就是幅度值），其实就是相当于得到了一个左右上下全都对称的矩阵，因此，对一张图片做离散傅里叶变换，往往是这样的结果。

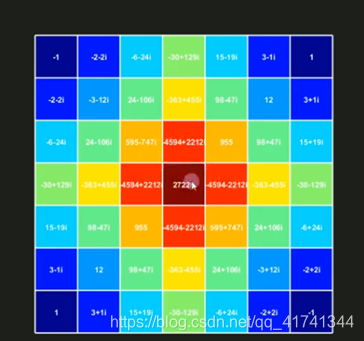
（6）改变频谱图的中心点

改变了中心点以后，高频区域分布到了四个角，低频区域到了中心，就会出现中心亮，四角暗的频谱图了

3. Opencv dft代码解析

在了解了离散傅里叶变换的整个过程和意义之后，我们来通过实际的Opencv代码来理解DFT。

3.1 导入图片

	//1.载入图片:应该是灰度图
	Mat m = imread("1.png",0);

3.2 计算最佳的边界长度

//2、计算最佳的边界长度
	Size dftsize;
	dftsize.width = getOptimalDFTSize(m.cols);
	dftsize.height = getOptimalDFTSize(m.rows);

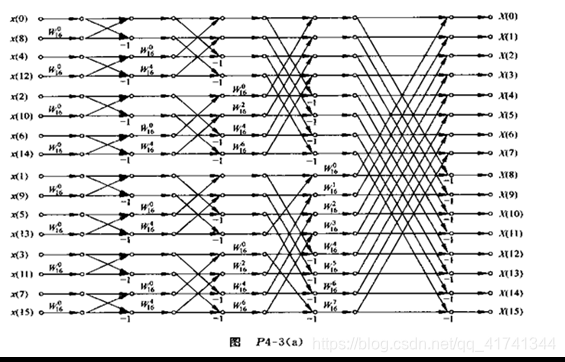
getOptimalDFTSize()函数用于获得最佳的边界值长度，从快速傅里叶变换（FFT)的角度来看，计算傅里叶变换的时候，两个共轭的数据可以组成一个蝶形计算单元，能够加快运算速度。所以如果边界点的数值合适的话，能够提高计算速度。官方说明是，当图片边界为2,3,5的倍数时，能够提高dft函数的计算速度。

3.3扩充边界

//3、扩充边界
	Mat Re(dftsize, CV_8UC1);
	copyMakeBorder(m, Re, 0, dftsize.height - m.rows, 0, dftsize.width - m.cols, BORDER_CONSTANT);

函数原型为：

void cv::cuda::copyMakeBorder	(	
	InputArray 	src,
	OutputArray 	dst,
	int 	top,	
	int 	bottom,
	int 	left,
	int 	right,
	int 	borderType,
	Scalar 	value = Scalar(),
	Stream & 	stream = Stream::Null() 

第一个参数：输入图片src
第二个参数：输出图片dst，输出图片的大小应该满足Size（src.cols+left+right,src.rows+top+bottom）
第三到第六个参数：沿上下左右扩充的像素点大小
第七个参数：边界类型，如果取值为BORDER_CONSTANT的时候，那么下一个参数就是填入的边 界值
第八个参数：默认值为0，可以认为是边界值

3.4 增加通道数

因为经过傅里叶变换之后，原来的实数矩阵会变成复数矩阵，为了能够储存复数量，必须增加一个通道，也就是说，傅里叶变换之后得到的那个矩阵，实际是一个CV_8FC2类型的矩阵，第一个通道是实数量，第二个通道是复数量。所以我们必须给输入矩阵增加一个通道

//4、增加通道
	Mat Im(dftsize, CV_8UC1, Scalar::all(0));

3.5 合并通道

因为傅里叶变换得到的数据，不但有正负，还有浮点数，数据还都很大，原来储存像素点的uchar类型无法做到储存这些数据。因此，必须转换成float类型的数据进行傅里叶变换，在此处就做了数据类型转换。

	//5、合并实部和虚部
	vector<Mat> temp = { Mat_<float>(Re),Mat_<float>(Im) };//要做数据类型转换，从uchar变成float
	Mat out(dftsize, CV_32FC2);
	merge(temp, out);

3.6 傅里叶变换

//6、进行离散傅里叶变换
	dft(out,out,0,0);

3.7 求幅值

因为最后绘制的频谱图是一个单通道灰度图，如果想通过像素点的量暗来观察频谱，就必须转换成幅值图像。这个函数的作用就是求的前两个输入矩阵的根下平方和，赋值给输出矩阵。

//7、从复数图中分离出实部和虚部，并且求他们的幅值
	vector<Mat> channels;
	split(out, channels);
	Mat rst;
	magnitude(channels.at(0), channels.at(1), rst);

3.8 取对数

因为灰度图只有0-255个数据，而明显经过傅里叶变换以后的矩阵数值不是这个范围，所以我们通过取对数的方法，减少这个数据大小，并且通过下一步的归一化，把所有数据变成0-1的范围，方便显示

//8.把数字取对数，变小
	log(Scalar::all(1) + rst,rst);

3.9 归一化

经过归一化之后的图像，呈现的结果就是那种四角亮，中心暗的频谱图了，如果想把原点变到中心，就还要进行下一步操作

//9.归一化
	normalize(rst, rst, 0, 1, NORM_MINMAX);
	imshow("a", rst);

3.10 中心点转移

这一步首先做了一个操作就是把图像边长边长偶数，通过与-2进行按位与运行。

为什么与-2按位与可以获得偶数呢？因为-2的二进制是11111110（假设只有8位），与任何一个整数进行按位与运算，都可以做到前面所有位都不变，最后一位变成0。而偶数和奇数的二进制区别不就是最后一位是1还是0吗。所以通过与-2按位与，能够把任何一个整数的最后一位变成0，也就确保了图像边长是偶数个像素点。

至于下面中心点转移使用的方法就是，把图片分成四个部分，左上角和右下角交换，左下角和右上角交换，即可得到最后的图片

//10、裁剪成偶数，并把原点转移到中心来
	rst = rst(Rect(0, 0, rst.cols & -2, rst.rows & -2));

	int width = rst.cols / 2;
	int height = rst.rows / 2;
	Mat roi1 = rst(Rect(0, 0, width, height));
	Mat roi2 = rst(Rect(width, 0, width , height));
	Mat roi3 = rst(Rect(0, height, width , height));
	Mat roi4 = rst(Rect(width, height, width , height));

	Mat exchange;
	roi4.copyTo(exchange);
	roi1.copyTo(roi4);
	exchange.copyTo(roi1);
	

	roi2.copyTo(exchange);
	roi3.copyTo(roi2);
	exchange.copyTo(roi3);
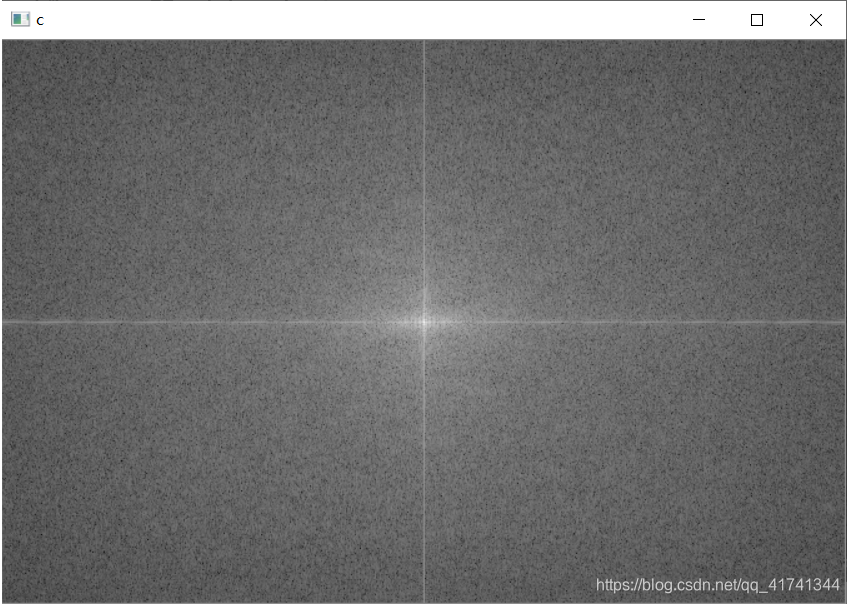
	imshow("c", rst);

频谱图未中心化：
频谱图中心化：

参考文献

[1] 深入理解离散傅里叶变换(DFT) https://zhuanlan.zhihu.com/p/71582795
[2] 2-Dimensional Discrete-Space Fourier Transform https://www.youtube.com/watch?v=YYGltoYEmKo&t=614s
[3] 二维傅里叶变换是怎么进行的 https://www.zhihu.com/question/22611929?sort=created
[4] How the 2D FFT works https://www.youtube.com/watch?v=v743U7gvLq0&t=475s
[5]离散傅里叶变换零基础入门-中文1（针对工科生，无需连续傅立叶变换知识）https://www.bilibili.com/video/av44600709?from=search&seid=15317105793432807268