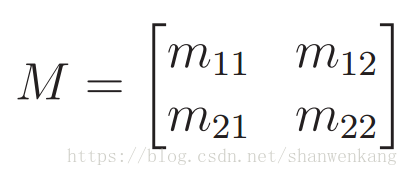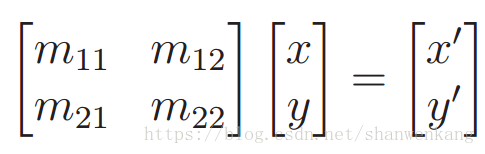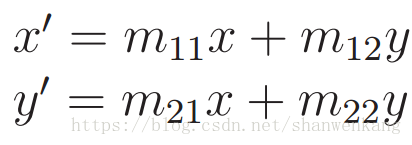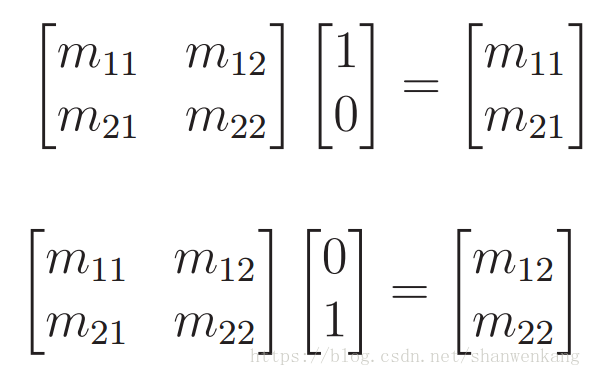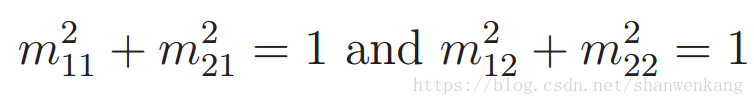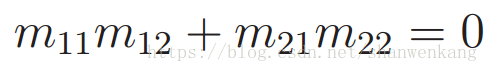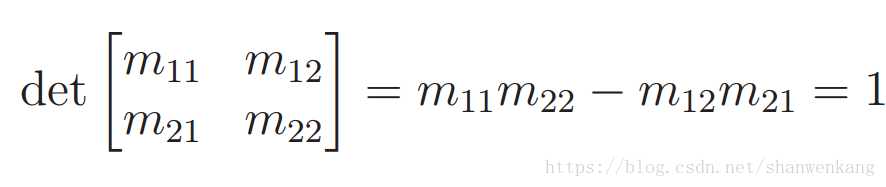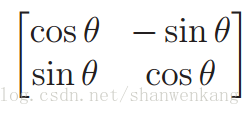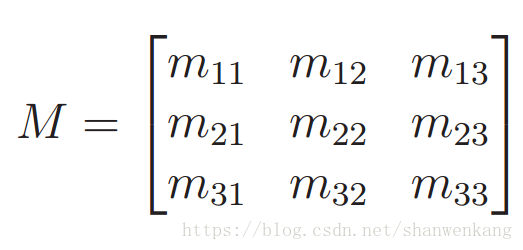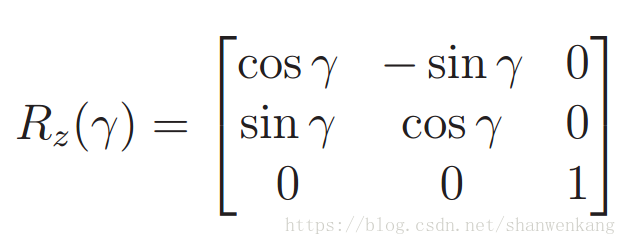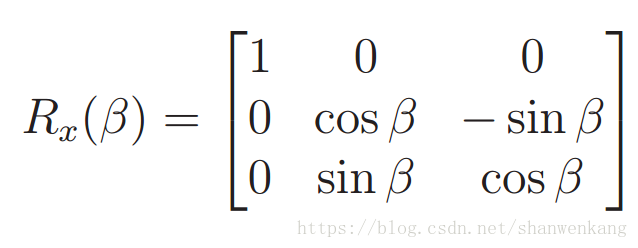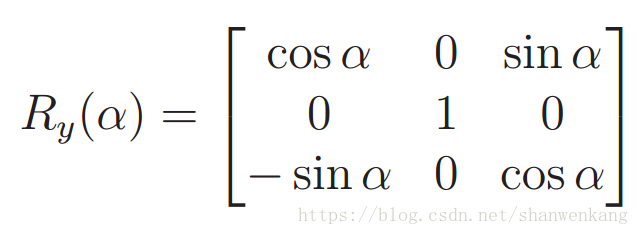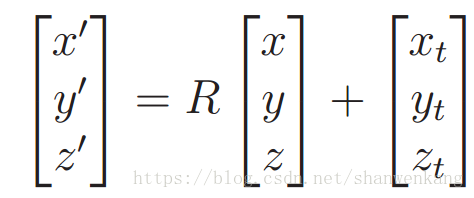Steven M. LaValle 的 Virtual Reality 这本书中讲了关于几何模型变换以及显示的知识,跟网上的资料比这本书里讲的比较简洁,于是想做一个总结。本博客参考了《Virtual Reality》的中文译版,翻译与校验人员: 上海交通大学媒体技术实验室(http://medialab.sjtu.edu.cn)
Part I
Part II
平移
考虑以下 3D 三角形
((x1, y1, z1), (x2, y2, z2), (x3, y3, z3))
顶点坐标表示为通用常量。
设 xt,yt 和 zt 是分别沿 x,y 和 z 轴的我们想要改变的三角形位置量。 改变位置的操作称为变换,由下式给出
(x1, y1, z1) → (x1 + xt, y1 + yt, z1 + zt)
(x2, y2, z2) → (x2 + xt, y2 + yt, z2 + zt)
(x3, y3, z3) → (x3 + xt, y3 + yt, z3 + zt)
其中 a→b 表示在变换之后 a 被 b 替换。
旋转——2D
考虑一个 2D 虚拟世界,其中的点坐标(x,y)。 你可以把它想象成我们最初的 3D 虚拟世界中的一个垂直平面。 现在考虑一个通用的 2x2 矩阵。
其中四项的每一个可以是任何实数。 我们看看当这个矩阵乘以点(x, y)后会发生什么,当它被写为列向量时。执行乘法,我们有
其中(x',y')是变换点。使用简单的代数,矩阵乘法产生
假设我们放置两个点(1,0)和(0,1)在平面上。它们分别位于 x 和 y 轴上,距离原点的距离(0,0)一个单位。使用向量空间,这两点就是标准单位矢量(有时写为 i 和 j)。如果我们将它带入矩阵乘法中可以得到:
这些特殊点只选择 M 上的列向量。这意味着如果 M 应用于模型转换,则 M 的每一列确切地表示每个坐标轴是如何改变的,也就是说x轴变换成了(m11,m21)这个方向,y轴变换成了(m12,m22)这个方向。下图说明了将各种矩阵 M 的变换效果。
对于上述M矩阵中只有一部分是有效的旋转,因为为了确保模型不会被扭曲,要求M满足下列条件:
1.没有伸展的轴。
2.没有剪切。
3.没有镜像。
为了满足第一条规则,M 的列必须有单位长度
为了满足第二条规则,必须保证转换后的坐标轴垂直。否则,会发生剪切。由于 M 的列表示轴是如何变换的,那么此规则意味着它们的内部(点)积为零,也就是x轴的变换(m11,m21)与y轴的变换(m21,m22)垂直:
满足第三条规则要求 M 的行列式是正数。当满足前两条规则后,唯一可能的行列式是 1(正常情况下)和-1(镜像情况)。 因此,该规则意味着:
第一个约束条件表示每列必须都被选择以使它每个元素位于一个以原点为中心的单位圆上。在标准的平面坐标,我们通常将这个圆的方程写作 x^2 +y^2 = 1,在极坐标下可以得x = cosθ y = sinθ。我们用角度θ代替点的坐标(x, y),令 m11=cosθ m21= sinθ,M可写做:
这样通过θ的变化(0~2π范围内),就可以表示所有的 2D 旋转。
接下来我们讨论旋转的自由度(DOF)。一开始的时候,矩阵 M 的四个元素是可以任意取值的,也就是说有 4 个自由度。第一个约束条件减少两个自由度,第二个条件也减少一个自由度,第三个条件并没有减少自由度,它只去掉了一半可能的变换,因为这些变换是另一半的镜像翻转。 最后, 我们得出结论, 2D 旋转只有一个自由度, 由参数θ决定; 而且,这些旋转都可以用单位圆的点来表示
旋转——3D
现在我们尝试将 2D 旋转的模式扩展到三维空间中,旋转矩阵的三维形式如下所示,包含 9 个元素:
因此,一开始 3D 旋转有着 9 个自由度,同样的,我们也要知道一个合法的 3D 旋转需要哪些限制条件。首先,每一列必须保证是单位长度。例如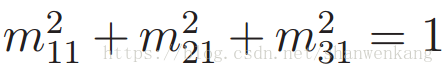
最后,我们得到了一系列满足代数约束的矩阵,然而,和 2D 旋转不同,它并不能用单位球面上的点来表示。我们只知道它有 3 个旋转自由度,意味着它应该可以由 3 个独立的参数来表示,旋转矩阵M中的 9 个元素均可由这 3 个参数计算出,因此我们通过构建几个 2D 旋转变换来描述 3D旋转。
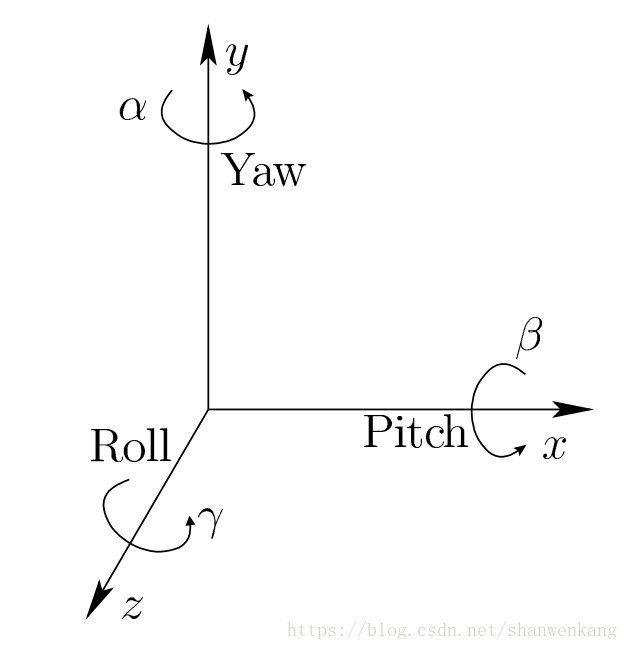
用翻滚角(roll) 来表示绕 z 轴逆时针方向的旋转γ,用俯仰角(pitch) 来表示绕 x 轴的逆时针旋转β,用偏航角(yaw) 来表示绕 y 轴的逆时针旋转α,旋转矩阵如下:
偏航角、俯仰角、翻滚角经过组合可以表示所有可能的 3D 旋转:
需要注意的是矩阵乘法是“后向的”,也就是说对一个向量p进行旋转的时候是将它左乘矩阵,因此旋转RQp是先用Q进行旋转,然后再用R进行旋转。还需要注意的是上式中的顺序不可颠倒,因为它不满足交换律。例如,先旋转π/2 的偏航角,再旋转π/2 的俯仰角与先旋转俯仰角再旋转偏航角的结果是不一样的。
平移+旋转
我们用一个旋转矩阵 R 进行旋转,紧接着平移(xt, yt, zt),代数形式如下所示:
如果可以通过一次操作同时完成平移和旋转,那我们使用起来将会方便很多。尽管我们没有办法通过一个 3x3 的矩阵完成如上操作,但是我们可以增加矩阵的维度,用一个 4×4 的齐次变换矩阵来表示。
符号Trb指代一个做刚体变换的矩阵,也就是说,不包含扭曲变形。一个齐次变换矩阵可能包含其他种类的变换。因此一个原始点经过平移加旋转可以表示为
我们经常会想要进行反变换,对于平移变换(xt, yt, zt),只需简单地对其取相反数(‐xt, ‐yt, ‐zt)即可;对于一般的矩阵变换 M,我们取它的逆 M‐1(如果存在)。这计算起来通常很复杂,但幸运的是,对于我们所研究的情况,它们的逆计算起来要简单很多。对于旋转矩阵 R, 取逆的过程相当于取它的转置 R‐1=RT。 对于上述, 它的反变换写为:
经过上述过程就可以将矩阵的平移与旋转用一个4×4的矩阵表示了