计算机图形学整理

色彩视觉

色彩是对不同波长的光的能量的感知：

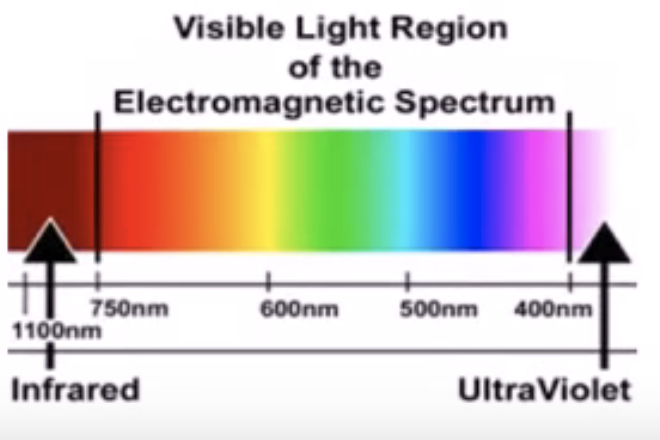
1. 不同波长的电磁波(electromagnetic waves)对应不同的色彩；
2. 对于人眼能感知的光(可见光)，其波长范围为380nm到760nm之间。

光的谱分布

1. 光是由不同波长的电磁波按照某种能量分布混合叠加而成。例如，白光是由所有可见波长的电磁波以相等的强度混合得到。
2. 谱分布：光在各个可见波长的分量的强度分布函数称为光的谱分布。

光在每个波长上的能量有多大，就得到了上图中的一条曲线，这个曲线就是谱分布。我们可以用这条曲线来刻画一些特有的光。

1. 与光类似，色彩也可以使用谱分布函数来进行描述。
2. 然后，使用谱分布函数来表示色彩，不仅复杂，而且这样的表示方法并不是一个一一对应关系。
3. 实际上，不同的谱分布函数可能对应为同一种色彩，也就是异谱同色现象。

RGB色彩空间

• 在所有用于表示色彩的各种色彩空间中，RGB(红绿蓝)色彩空间在计算机图形学中的使用最为广泛：

1. 色彩使用三通道RGB向量(r,g,b)来表示；
2. 在RGB色彩空间中，有部分的常用操作可以通过对RGB三通道分别处理而进行；
3. 通常可以将r、g、b分别规整化为[0,1]内的浮点数；当使用8bit进行存储时，r、g、b通常取值为[0,255]内的整数。

• 色彩被表示成三个基本色彩：红色(R)、绿色(G)、蓝色(B)的线性组合：

1. C = rR + gG + bB
2. 为什么选择红绿蓝作为基本色彩？
   1. 以人类视觉的三刺激理论为基础；
   2. 人眼的视网膜中有三种锥状视觉细胞，分别对红、绿、蓝三种光最敏感。

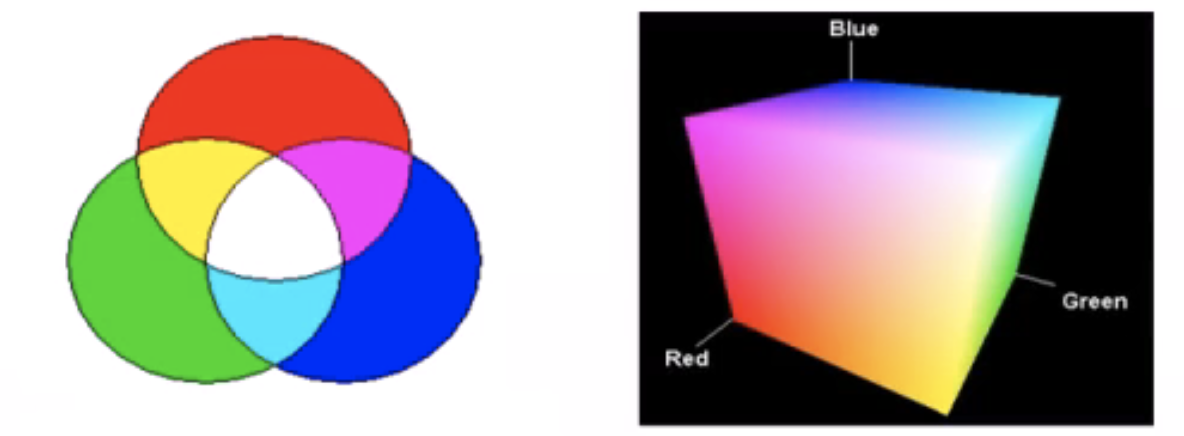
我们可以近似把所有的颜色看成是一个立方体，立方体的三个轴对应R、G、B的值，那么它们在立方体空间中的每一个点都有一个(r,g,b)值对应一种颜色。

• 然而，一部分色彩无法表示成R、G、B光波的正线性组合，这是RGB色彩空间的一个缺点。

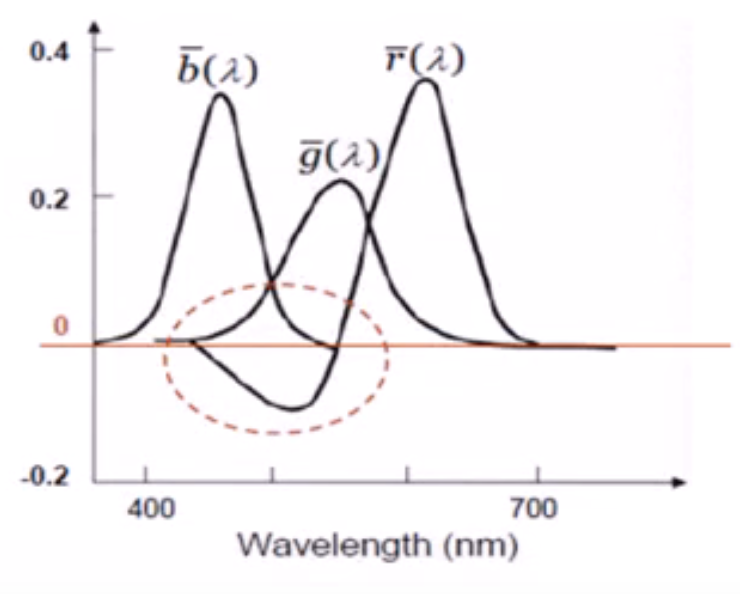
上图是红、绿、蓝的三根曲线，当波长为600的时候，可以由红色和绿色曲线的两个交点组合而成的波长为600的光，这里是正常的；但是波长为500的时候，红色光的取值为负，它无法使用正线性组合来表示，这是一个问题。国际标准化组织就引入了另外的色彩空间做修正来使得R、G、B都是正的。

• 其他常用的色彩空间还包括：

1. CMY
2. HSV
3. CIE XYZ

CMY色彩空间

CMY是不同于RGB的另外一种基本色彩。它是由青(Cyan，1-红色)、品红(Magenta，1-绿色)、黄(Yellow，1-蓝色)组成，它们分别是R、G、B的补色(complements)。

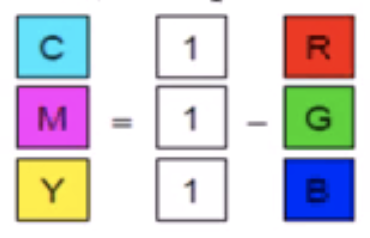
1. CMY被称为“减色系统”，(0,0,0)为白，(1,1,1)为黑；数值越大越灰暗。
2. RGB为“加色系统”，(0,0,0)为黑，(1,1,1)为白。数值越大越鲜艳。

CMY主要用于印刷出版行业使用。

HSV色彩空间

1. 在真实的RGB彩色图像中，可以包含多达256*256*256=16777216种可能的色彩；
2. 使用RGB色彩空间来描述和定位如此大量的不同色彩非常困难，也不直观。HSV系统则提供了一个直观的方法来对色彩进行准确的选择；
3. HSV色彩空间应用于：图像处理、分形图像、光线跟踪...

HSV的具体内容可以参考OpenCV计算机视觉整理 中的HSV/HSB/HSL。

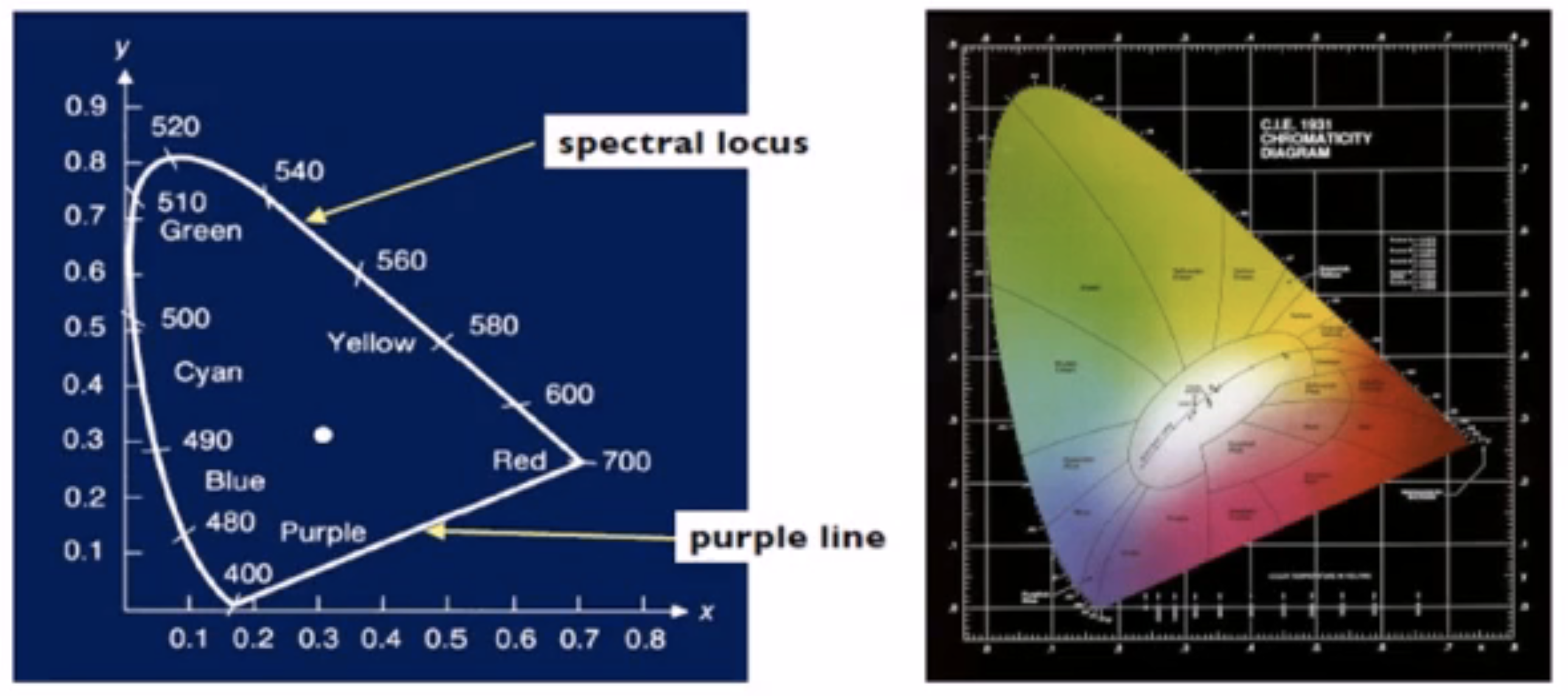
CIE XYZ色彩空间

由国际发光照明委员会于1931年提出。

CIE XYZ色彩空间可以表示所有可感知的色彩(而RGB空间却不能)。

1. 色彩基XYZ是色彩基RGB的线性变换。
2. 更多地应用于色彩科学的研究。
3. 于人类的感知系统密切相关。

可以把CIE XYZ色彩空间可视化为如下色度图，其中x=\(X\over X+Y+Z\)，y=\(Y\over X+Y+Z\)

图像和像素

图像

1. 图像可以看成是一个二维离散函数f(x,y)；
2. 函数f的定义域是由矩阵排列着的许多格子组成，这些格子被称为像素(pixel)；
3. 函数f的取值则为各个像素的色彩；对于彩色图像，可以是RGB或者RGBA；对于灰度图像，f为单值函数。

三角网格模型

图形学的基本目标是什么？

1. 从虚拟的三维场景及相机的位置信息中，生成出一副二维图像。
2. 而三维场景又以怎样的数据结构来表示？
   1. 简单的球体，长方体可直接用其参数描述；
   2. 对于复杂模型，则需要使用参数曲线和曲面或者更一般的网络模型来进行描述。
   3. 网络模型中又以三角网格最为常用。
3. 三角网格是由一系列欧式空间中的三维顶点以及连接这些顶点的若干三角面片组成，具体包括：
   1. 顶点集合 V=(\(v_1,v_2,...,v_n\))
   2. 面片集合 F=(\(f_1,f_2,...,f_m\))
   3. 其中F中的每个面片\(f_i\)都是由V中的顶点构成的空间三角形：\(f_1=(v_{a1},v_{b1},v_{c1}),f_2=(v_{a2},v_{b2},v_{c2}),...\)

上图中的牛显示了三角网格的结构，龙和人头也是使用三角网格绘制的结果。

法向量

三角面片的法向量(normal):

1. 三角面片的法向量是垂直于该三角面片所在平面的非零向量；
2. 对于每个三角面片单独而言，其法向量都有两种可能的朝向；
3. 法向量的朝向决定了一个三角面片的正面与反面；
4. 对于连续可定向的三角网格整体而言，相邻的三角面片需要具备一致的法向量朝向。

光照模型

光照模型(lighting model或illumination model)用于计算光的强度

1. 局部光照明(Local Lighting)，关注物体直接受到光源影响所产生的光照效果。
2. 全局光照明(Global Lighting)
   1. 关注阴影效果；
   2. 关注所有不是直接与光源位置相关的光照效果，例如反射和折射效果，等等...

光照模型的历史

1. 1967年，Wylie等人第一次在显示物体时加入了光照明效果，认为光的强度与物体到光源的距离成反比关系。
2. 1970年，Bouknight提出了第一个光反射模型：
   1. Lambert漫反射光+环境光
   2. 发表于Communication of ACM
3. 1971年，Gouraud提出了漫反射模型加插值的思想：
   1. Lambert漫反射光+Barycentric插值
   2. 发表于IEEE transactions on Computers
4. 1975年，Phong提出了图形学中第一个有影响也是最有影响的光照模型：Phong模型
   1. 漫反射(diffuse light)+环境光(ambient light)+高光(specular light)
   2. 发表于Communication of ACM

光的传播

• 光的传播遵循反射定律：

1. 入射角等于反射角；
2. 入射光线、反射光线、以及反射面的法向量位于同一平面内。

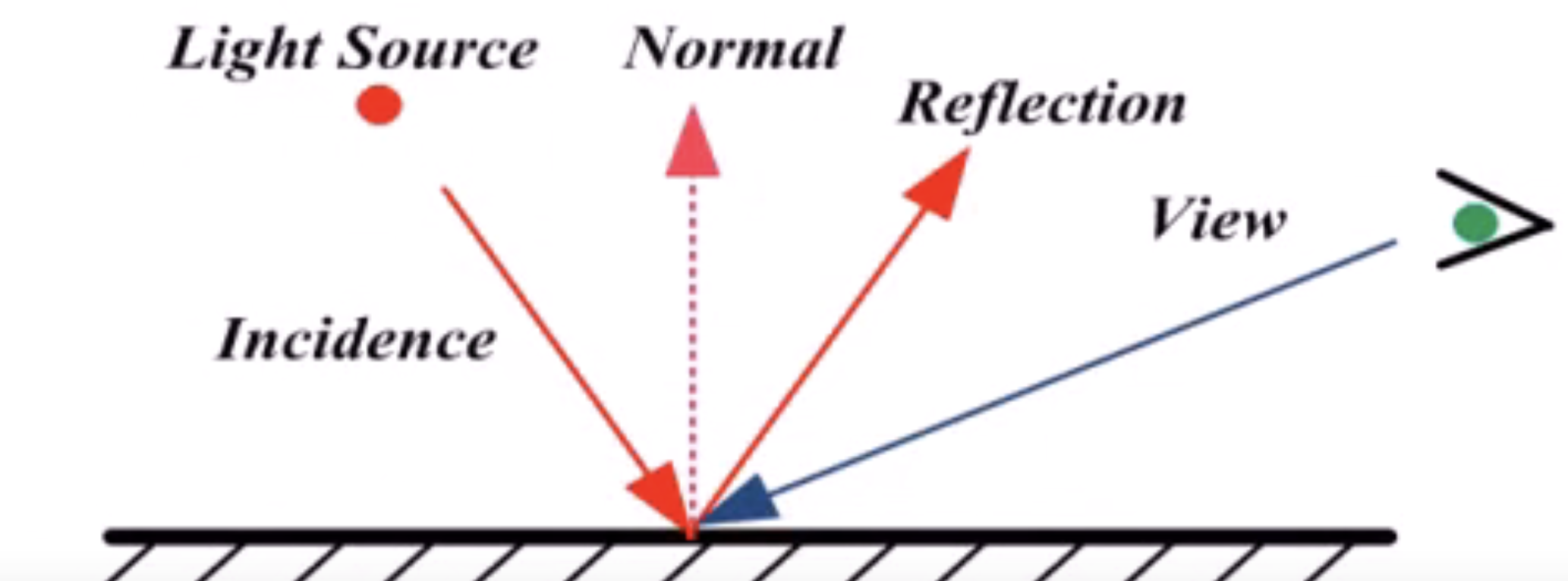
上图中，右边的绿点表示眼睛，Light Source表示光源，Reflection是反射光，Normal是法向，View是视点。它们都是位于同一个平面的。

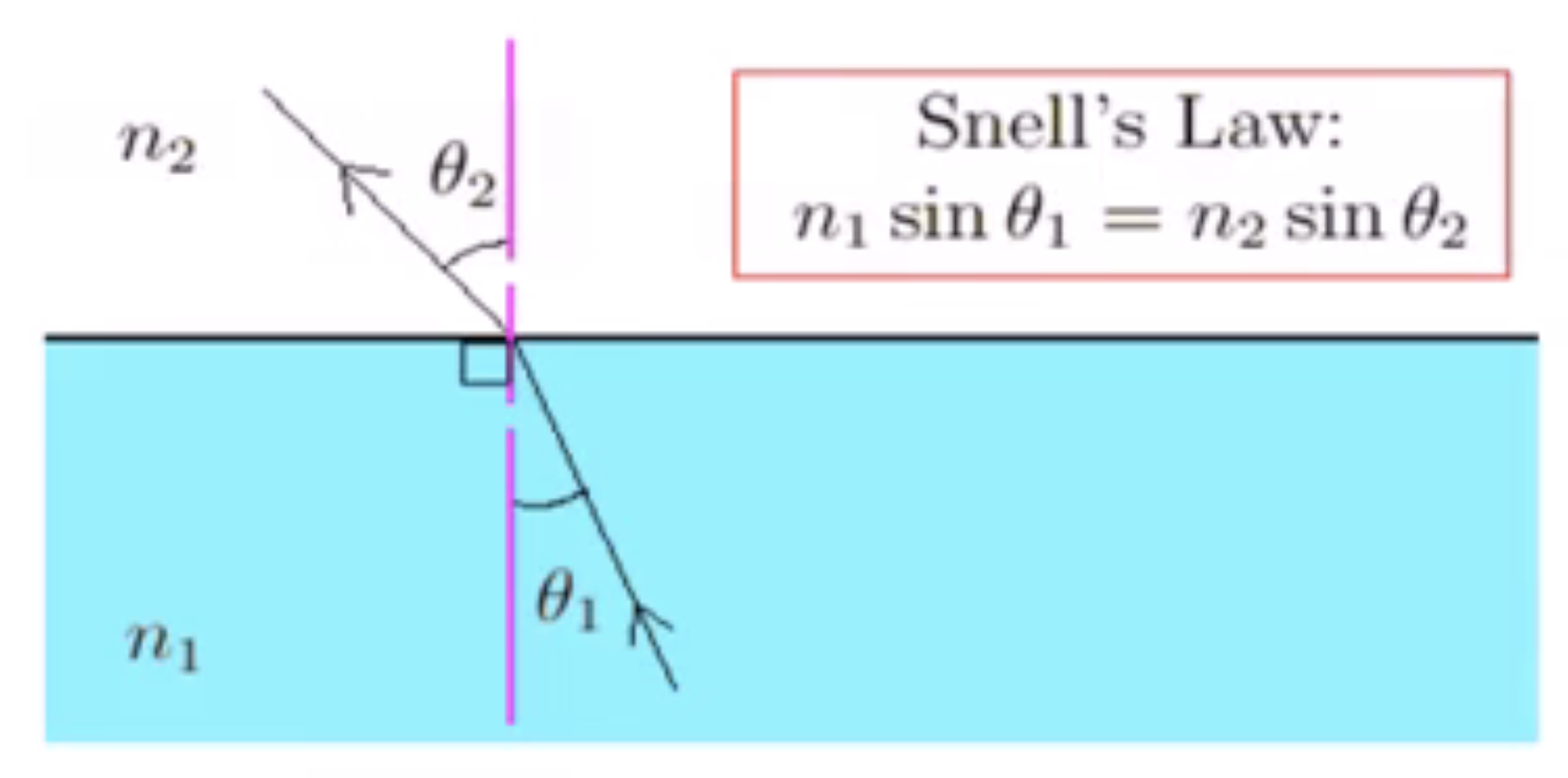
• 折射定律(也叫Snell定律)：

1. 入射角和反射角的正弦值之比是一个仅仅取决于介质的常数；
2. 这个常数称为相对折射系数。

• 光的传播遵循能量守恒定律：

\(I_i = I_d + I_s + I_t + I_v\)

1. \(I_i\)：入射光的能量
2. \(I_d\)：漫反射光的能量
3. \(I_s\)：镜面反射(specular reflection)光的能量
4. \(I_t\)：折射(refraction)光的能量
5. \(I_v\)：被介质和物体所吸收的能量

• 光的度量方法

1. 立体角(Solid Angle):
   1. 衡量物体相对于某一视点P的视角大小；
   2. 立体角最大为4π。
   3. 
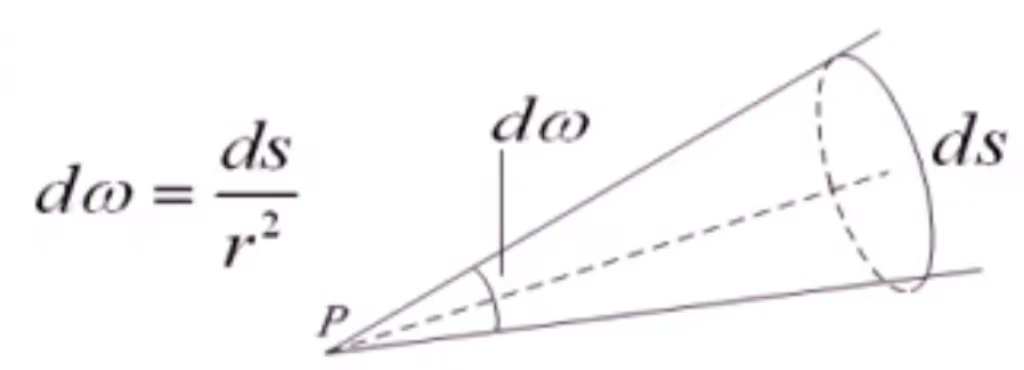
   4. 在上图中，使用空间一个面片的面积除以面片中心点到视点的距离的平方来表示立体角。空间最大的角度就是球，球的面积除以半径平方，得到最大立体角4π。平面角度最大是2π。
2. 光通量(Luminous Flux):
   1. 光通量定义为：单位时间内通过面元dS的光能量，记为dF。
3. 发光强度(Radiance):
   1. 发光强度定义为：单位立体角内的光通量，记为I。

Phong光照模型

Phong模型支持点光源和方向光源。

Phong模型是局部光照模型，将局部光照明效果分解为三个部分：

1. 漫反射光效果；
2. 镜面反射光效果；
3. 环境光效果。

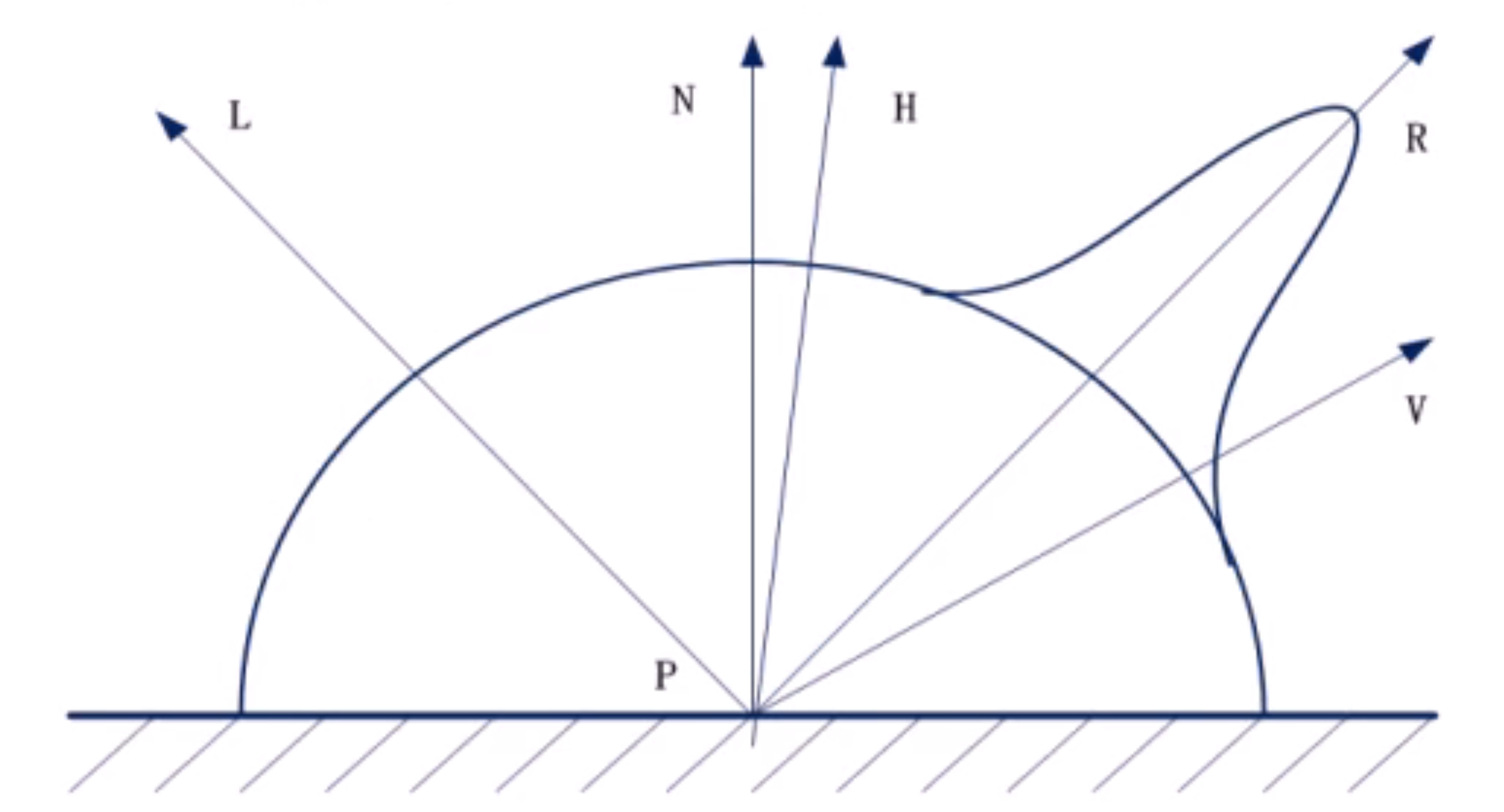
上图中，L是入射光，R是反射光，N是物体表面法向量，V是视点方向，H是L和V夹角的角平分线方向。

• 漫反射光效果

1. 漫反射光的传播是各向同性的；
2. 漫反射光的强度为：

\(I_d = I_iK_d*(L⋅N)\)

1. \(I_i\)是入射光强度
2. \(K_d\)是漫反射系数，它具有三个分量\(K_{dr}\)、\(K_{dg}\)、\(K_{db}\)，分别代表R、G、B三个通道的漫反射系数。
3. \(K_d\)与模型自身的色彩紧密相关。
4. L是入射光方向，N是法向。

该公式说明，物体表面上的一点，它的光强(颜色)主要取决于入射光和法向的夹角，该夹角越小，则光强越强，夹角越大则越弱。这就比如说中午的太阳光照比晚上的要强。

• 镜面反射光效果

1. 对于光滑的平面，依据反射定律，反射光线往往集中在一个小的立体角内，就是上图中反射光周围的一个凸起部分，这些反射光我们称之为镜面反射光；
2. 镜面反射光的强度为：

\(I_s = I_iK_s*(R⋅V)^n\)

1. \(K_s\)是镜面反射系数，与物体表面光滑度相关；
2. n是反射指数：n越大，则高光区域越集中。

R是反射光，V是视角，反射光线和视角的夹角如果为0表示反射光正好打到眼睛里。因为物体表面有粗糙度，不是完全光滑的，所以光线反射的时候不一定严格的局限在反射方向上，相邻的地方也能看到反射光的影响。

• 环境光效果

环境光的强度为：

\(I_a = I_iK_a\)

1. \(K_a\)是物体对环境光的反射系数。

其他因素产生的光统称为环境光。这样就得到了Phong模型。

• 视角光强度

视角方向的发光强度为漫反射光分量、镜面反射光分量，以及环境光分量的发光强度之和：

I = \(I_iK_a + I_iK_s*(R⋅V)^n + I_iK_d*(L⋅N)\)

上图是Phong模型中，这三种光的效果。叠加后的效果如下

调节不同的参数所产生的效果如下

明暗处理(shading)

考虑到物体表面的几何细节往往并不规则，为了减缓由模型离散化所导致的不光滑的色彩效果，通常的明暗处理除了使用光照模型外，还需要进行插值。

如果图像的每个点都算一个颜色的话，面片与面片之间有一个问题，人眼有一种马赫带效应，会夸大相邻两个面片的颜色的差异，如果一个模型是由很多面片表示的，一旦绘制出来之后，就变得棱角分明，很难看。所以我们必须给其做插值，做光滑。

Gouraud明暗处理和Phong明暗处理：

1. Gouraud明暗处理是对色彩进行插值；
2. Phong明暗处理则是对法向进行插值。

• Gouraud明暗处理

由Gouraud于1971年提出，又被称为Gouraud插值。

计算方法：

1. 首先计算所有模型顶点的色彩值；
2. 对模型上的任何一点，按照其所在的三角面片上顶点的色彩值按重心插值(Barycentric Interpolation)的结果赋予其色彩值。

• Phong明暗处理

由Bui Tuong Phong于1973年在他的博士论文中提出。与Phong光照模型是不同的概念。

计算方法：

与Gouraud明暗处理不同，Phong明暗处理不是对色彩插值，而是对点的法向量进行插值，得到连续的法向量场，再利用该法向量场逐点使用光照模型进行色彩的计算。

视点变换和视点方向

1. 图形学关注于如何将由几何模型组成的三维场景绘制成高质量的彩色图像。
2. 变换在图形学中至关重要：通过变换，可以简洁高效地设置和编辑三维场景，光照位置，以及是视点方向。

• 变换(Transformation)

1. 变换是一个将空间中的点x映射成其他点x'的函数。
2. 广泛应用于：Morphing(一个物体变成另一个物体，如猫变老虎)，Deformation(同一个物体的变形，如老虎变大一点，变长一点，眼睛变威武一点)。

• 简单变换

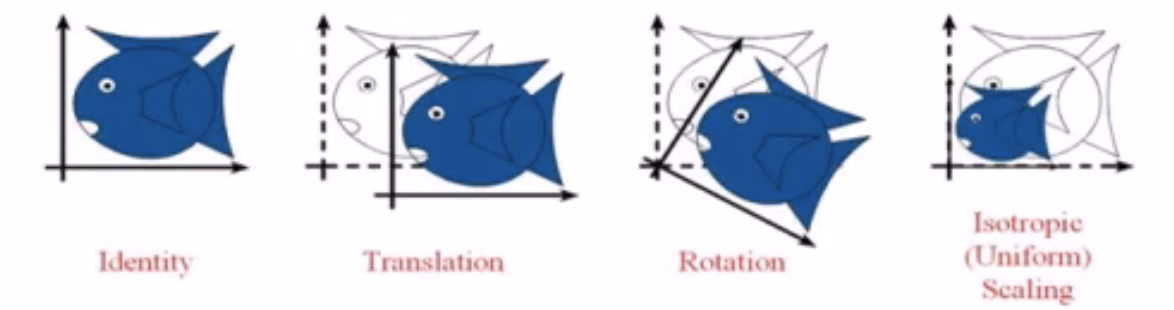
1. 从左到右的变换分别是：不变(Identity)、平移(Translation)、旋转(Rotation)、均衡缩放(Isotropic scaling)
2. 变换可以相互复合和嵌套：例如先旋转，再缩放，最后再平移。
3. 简单变换都是可逆的。

• 变换分类

常见的变换有如下几类：

1. 刚体变换(Rigid-body Transformation)
2. 相似变换(Similarity Transformation)
3. 线性变换(Linear Transformation)
4. 仿射变换(Affine Transformation)
5. 投影变换(Projective Transformation)

• 刚体变换

保持度量(长度、角度、大小)

刚体变换包括：

1. 不变
2. 平移
3. 旋转
4. 以及它们的组合

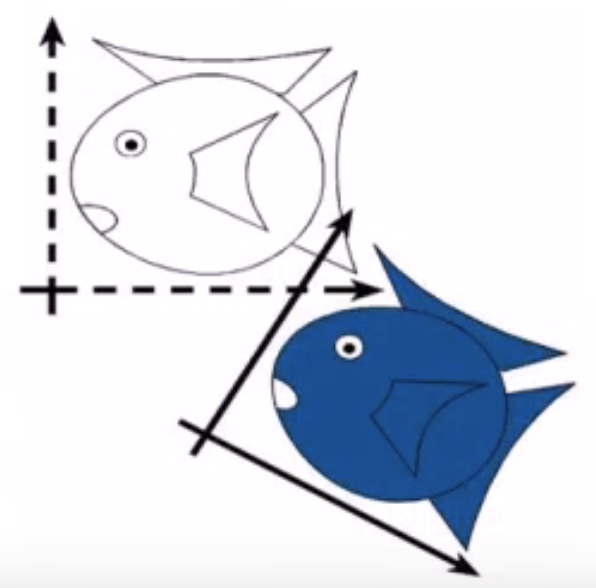
• 相似变换

保持角度。

相似变换包括：

1. 不变
2. 平移
3. 旋转
4. 均衡缩放
5. 以及它们的复合

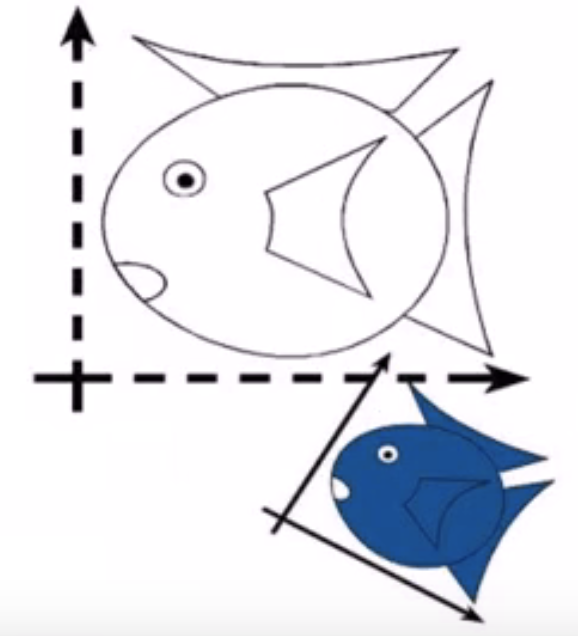
• 线性变换

线性变换满足如下方程：

L(p+q) = L(p) + L(q)           αL(p) = L(αp)

线性变换包括：

1. 不变、旋转、缩放(不一定要均衡缩放)
2. 对称(Reflection)，错切(Shear)

• 仿射变换

保持直线以及直线与直线的平行。两条在仿射变换之前平行的直线，在仿射变换之后依旧平行。

仿射变换包括：

1. 线性变换
2. 相似变换
3. 以及它们的复合

• 投影变换

保持直线

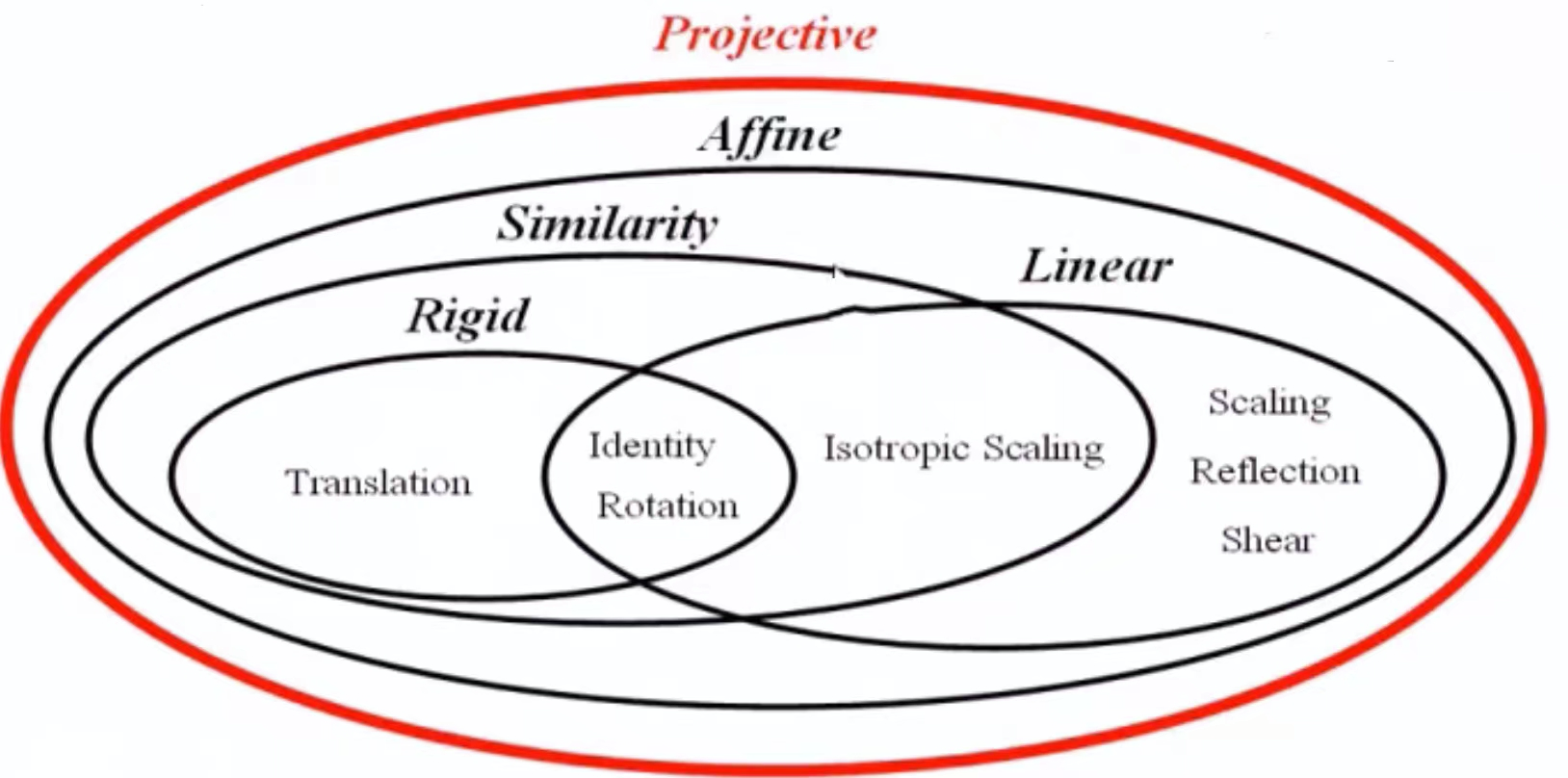
上图是投影变换的关系图

• 变换的表示

考虑简单的二维仿射变换(x'、y'是变换后的坐标，x、y是原坐标)：

1. x' = ax + by + c   
2. y' = dx + ey + f    

可以将1、2统一地写成矩阵形式：

变换的表示涉及到了两个变量：M和t，M是变换矩阵，t是平移向量。

p' = Mp + t

p'是变换后的坐标向量，p是原坐标向量。

然而，使用齐次坐标(Homogenous Coor-dinates)来表示p和p'，则上述公式成为：

p' = Mp

其意思就是将平移向量t放入到变换矩阵M中，使得M增加一个维度。

• 齐次坐标

齐次坐标的本质是使用四维数组来表示三维空间中的点和向量。

本来是一个二维向量(x',y')，在齐次坐标中写成(x',y',1)；而变换矩阵由\(((a,d),(b,e))^T\)变为\(((a,d,0),(b,e,0),(c,f,1))^T\)。有关齐次的概念可以参考线性代数整理 中的齐次线性方程组。

由于引入了新的维度，我们使用4*4的作用矩阵，同时使用(x,y,z,w)来表示一个点或向量：

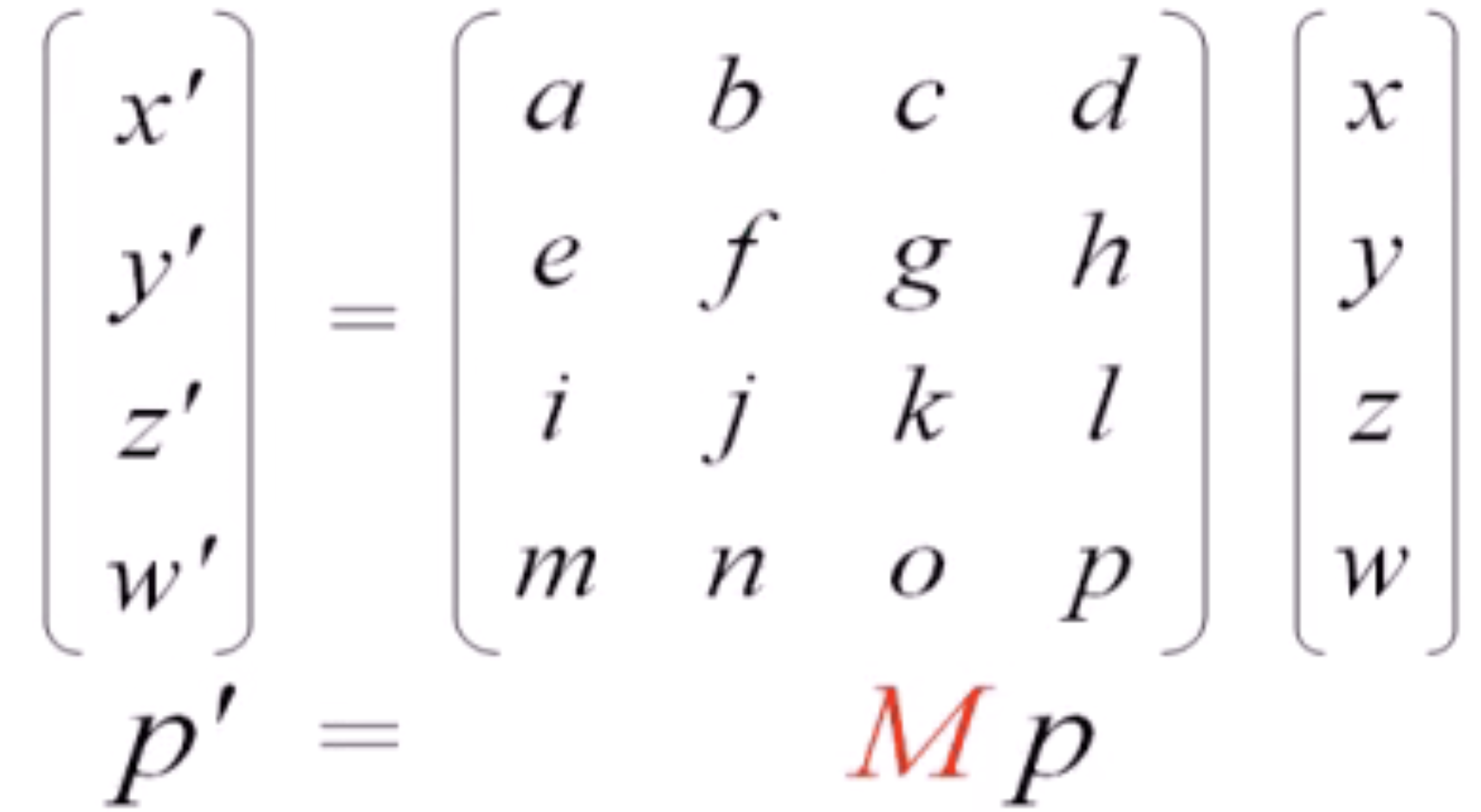
在大部分情况下w=1，可以忽略。

当齐次坐标被仿射矩阵作用时，w不会改变；而如果被投射矩阵作用时，w会改变。

齐次坐标的几何意义：

1. 当w非零时，通过将所有四个坐标同时除以w以归一化。例如(2x,2y,2z,2)等价于(x,y,z,1)。
2. 当w为零时，齐次坐标(x,y,z,0)可以理解为沿(x,y,z)方向的无穷远点。

• 平移变换(\(t_x,t_y,t_z\))的矩阵表达

在齐次坐标的框架下，平移变换可以表示成为简单的矩阵乘法：

有关这里的矩阵乘法的内容可以参考线性代数整理 中矩阵和向量的乘法

• 缩放变换(\(s_x,s_y,s_z\))的矩阵表达

以原点为缩放中心的缩放变换可以表示成为：

• 旋转变换的矩阵表达

三维空间中物体的旋转具有三个独立的自由度。

围绕z轴的旋转可以表示为：

围绕单位向量(\(k_x,k_y,k_z\))的旋转变换可以写成如下的Rodrigues公式：

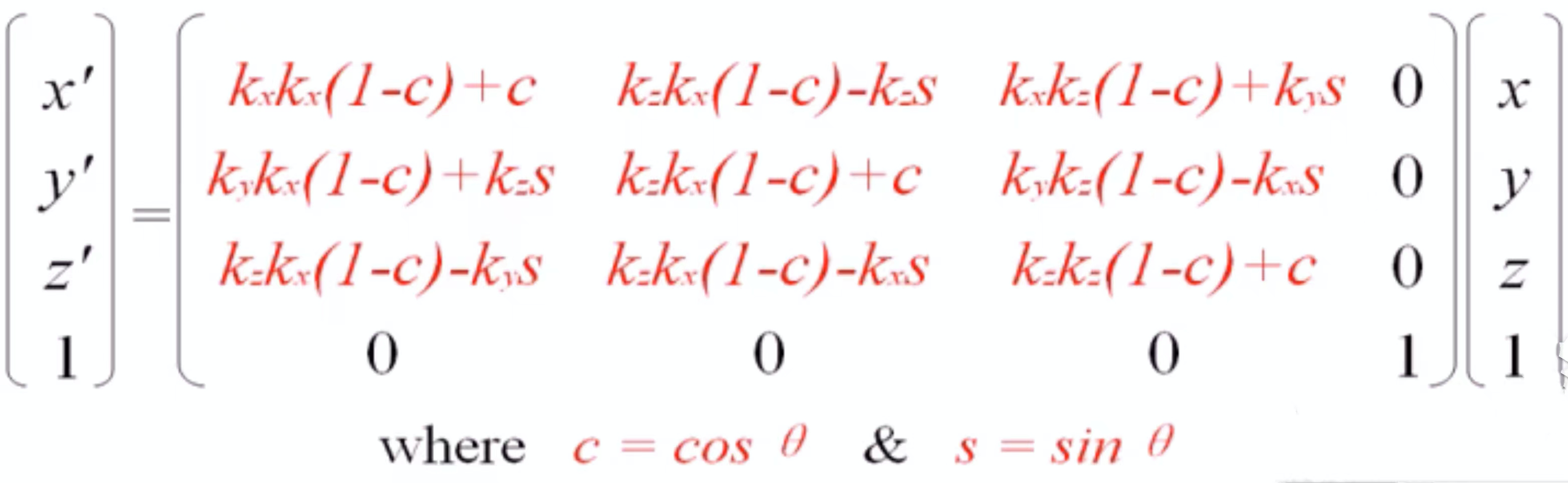
• 变换的复合(combination)

一个缩放和平移进行复合的例子：

复合等价于矩阵乘法：p' = T(Sp) = TSp

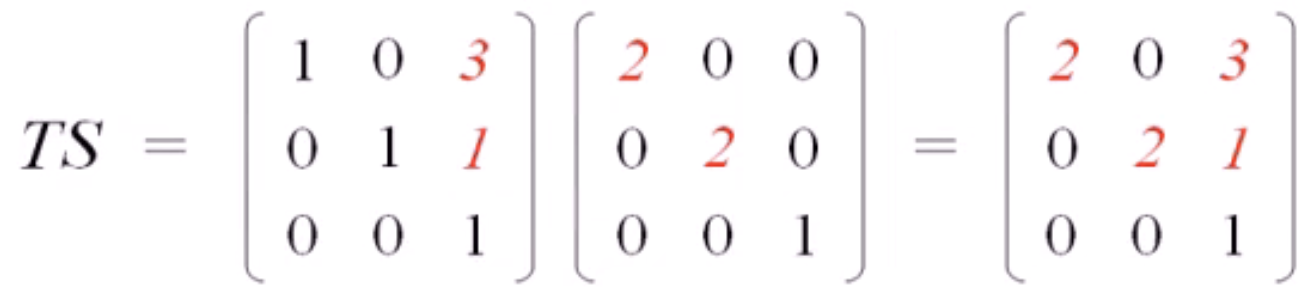
这里的矩阵乘法可以参考线性代数整理 中的矩阵和矩阵的乘法

先平移再缩放：p' = S(Tp) = STp

变换的复合不满足交换律，这是因为矩阵的乘法不满足交换律：TS ≠ ST

• 法向量变换

曲面的(单位)法向量是曲面与曲面正交的(单位)向量，它们是曲面最为重要的几何性质之一。

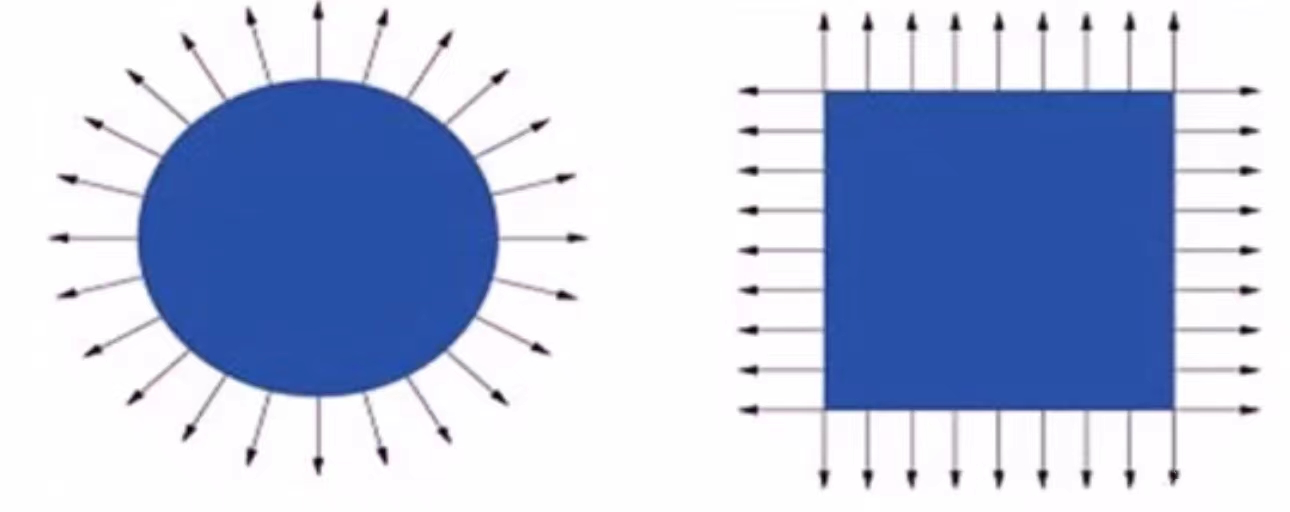
法向量是进行光照处理的必要输入，所有的光照模型都涉及到物体的法向量。只有知道了物体的法向量信息，才能绘制出具有三维立体感的图像。

在我们对物体进行变换时，法向量可以类似变换吗？我们发现，对于相似变换，法向量可以和物体使用同样的变换方程。

然后对于带有错切变换的仿射变换，同样的方程则不适用。

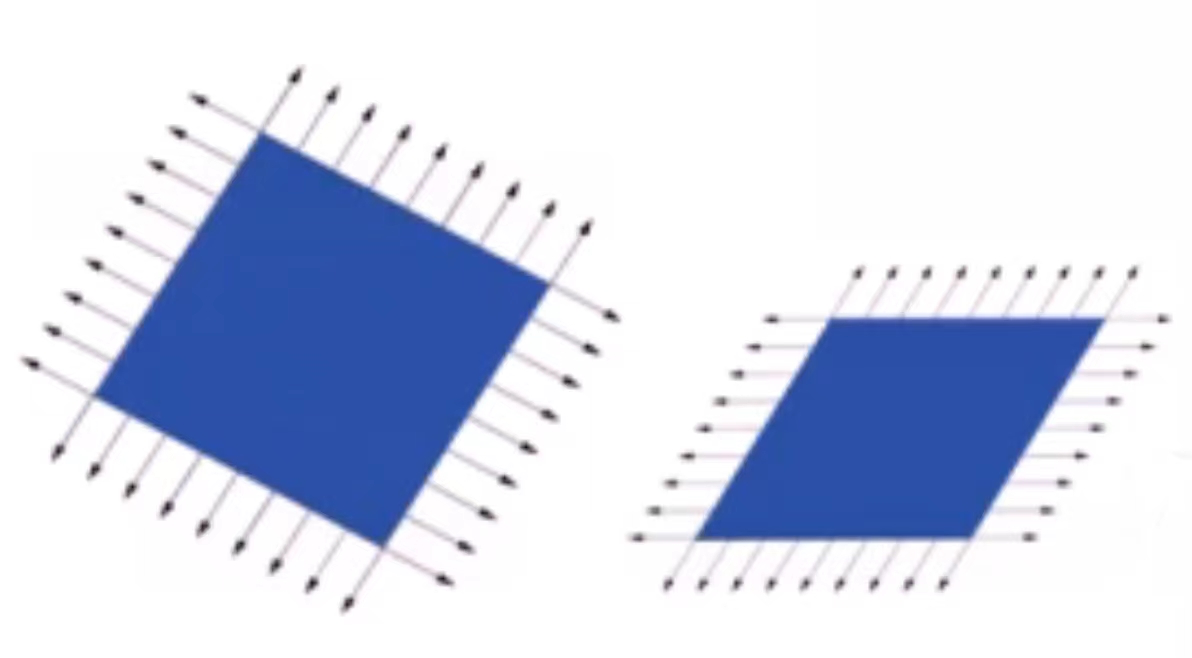
另一个例子(缩放)：对球做非均衡缩放，使用与物体同样的变换方程用于变换法向量会出现错误结果。

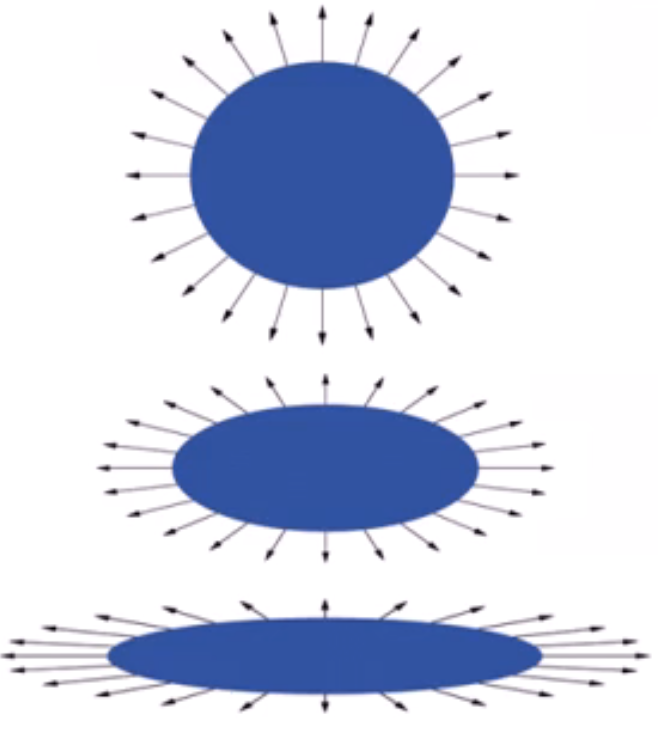
以下是错切和球正确的法向量变换

• 正确变换法向量

变换切平面(tangent plane)，再通过切平面结算法向量，而不是直接计算。

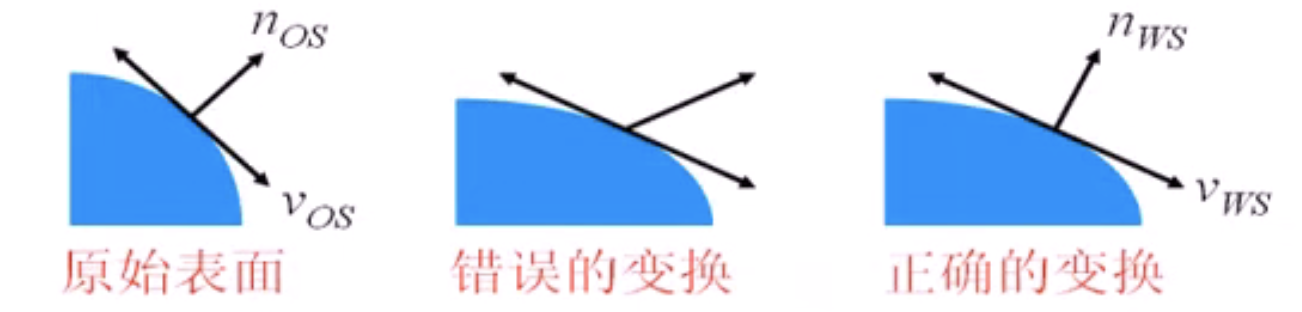
切平面上的任一向量\(v_{OS}\)变换后成为\(v_{WS}\):

\(v_{WS}\) = M\(v_{OS}\)

在上图中的原始表面，\(v_{OS}\)与\(n_{OS}\)垂直：

\(n_{OS}^T\)\(v_{OS}\)=0

\(n_{OS}^T\)(\(M^{-1}\)M)\(v_{OS}\)=0

(\(n_{OS}^T\)\(M^{-1}\))(M\(v_{OS}\))=0

(\(n_{OS}^T\)\(M^{-1}\))\(v_{WS}\)=0

正确变换上，\(v_{WS}\)与\(n_{WS}\)垂直：

\(n_{WS}^T\)\(v_{WS}\)=0，根据上面的推导，则有

\(n_{WS}^T\) = \(n_{OS}^T\)(\(M^{-1}\))

\(n_{WS}\)=\((M^{-1})^T\)\(n_{OS}\)

由此可见，法向量的变换矩阵是原变换矩阵的逆的转置。

视点和投影模式

1. 我们的眼睛能将三维场景感知为二维图像，大脑则会将二维图像再重构回三维。
2. 在计算机图形学中，我们利用投影，模拟眼睛的功能和效果。
3. 投影的两个重要概念：
   1. 视点变换：与相机位置及朝向相关。
   2. 投影模式：是将3D变换成为2D的变换模式，常用的包括正交投影和透视投影。

• 正交投影(Orthographic Projection)

1. 正交投影是视点在无穷远处的投影模式。
2. 缺乏立体透视效果。
3. 当xy平面是投影平面时，正交投影把(x,y,z)映射成(x,y,0)。

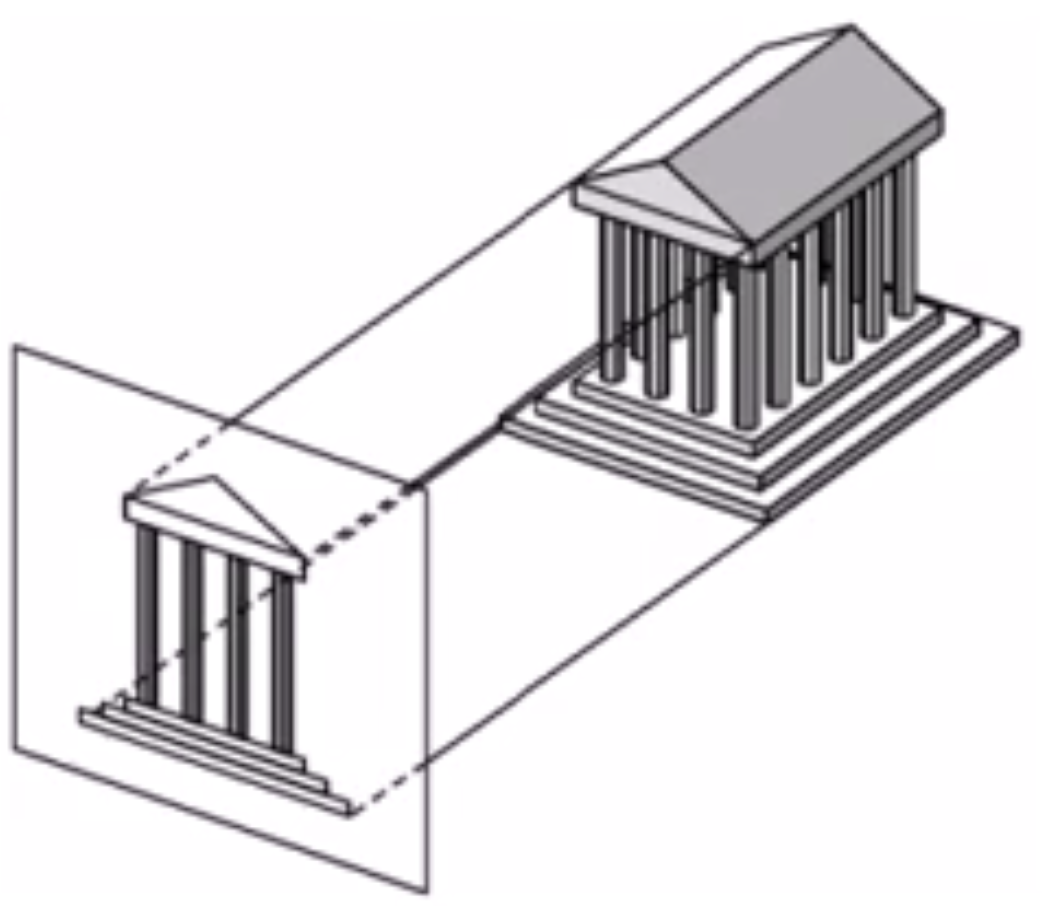
• 透视投影(Perspective Projection)

1. 透视投影是视点在有限距离处的投影模式。
2. 具有立体透视效果。
3. 当视点位于原点，投影平面为z=d时，透视投影把(x,y,z)映射成为((d/z)x,(d/z)y,d)。

透视投影矩阵

使用齐次坐标描述的透视投影变换可以写成矩阵形式：

T(x,y,z) = ((d/z)x,(d/z)y,d)

材质反射属性模型BRDF

双向反射分布函数(BRDF：Bidirectional Reflectance Distribution Function)

描述的是物体表面对光的反射性质。

• 球面坐标(Spherical Coordinate)

1. 由于光线主要是通过方向来表达，通常用球面坐标表达它们比用笛卡尔坐标更方便。
2. 球面坐标中的向量用三个元素来指定：
   1. r表示向量的长度
   2. θ表示向量和z轴的夹角
   3. φ表示向量在x-y平面上的投影和x轴的逆时针夹角

球面坐标与三维笛卡尔坐标(Cartesian Coordinates)之间的对应关系：

Car(x,y,z) = Sph(r,θ,φ)

转换公式为：

1. r = \(\sqrt {x^2+y^2+z^2}\)
2. θ = acos(\(z \over r\))
3. φ = atan(\(y \over x\))
4. z = r⋅cosθ
5. y = r⋅sinθ⋅sinφ
6. x = r⋅sinθ⋅cosφ

• 立体角(Solid Angle)

1. 立体角描述了从原点向一个球面区域张成的视野大小，是平面角在三维的自然推广。
2. 立体角的最大值为全角：4π，该最大值可以在区域为整个球面时取到。

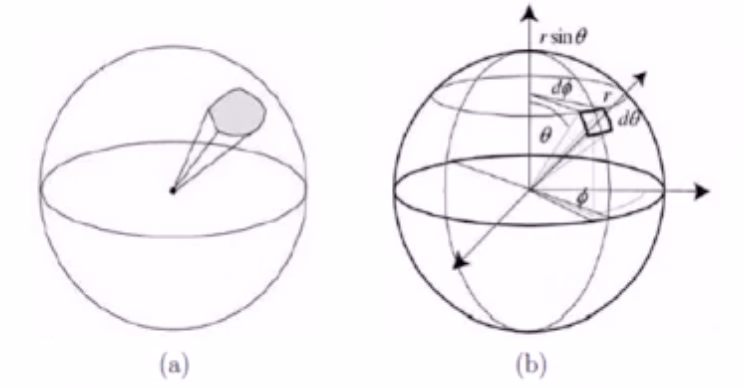
立体角ω具有如下微分形式：

dω = \(dA \over r^2\)

dA为球面面片面积，r为球体半径，由于面积微元(非常小的一块面积，类似于一元函数中的微分)在球面坐标系下可以写成：

dA = (rdθ)(r⋅sinθdφ) = \(r^2\)sinθdθdφ

这里主要看上图中的b图，我们首先可以把面片看成一个矩形，它的面积=长*宽；由于是面积微元，在球的经度上的弧长可以看成是矩形的一条边，那么根据弧长公式，就等于rdθ，dθ是该弧长的弧度。在球的纬度上的弧长，需要先找出纬度上的圆平面的半径，该半径=r⋅sinθ，该圆的弧度为dφ，那么该弧长就是r⋅sinθdφ

因此：

 dω = \(dA \over r^2\) = sinθdθdφ

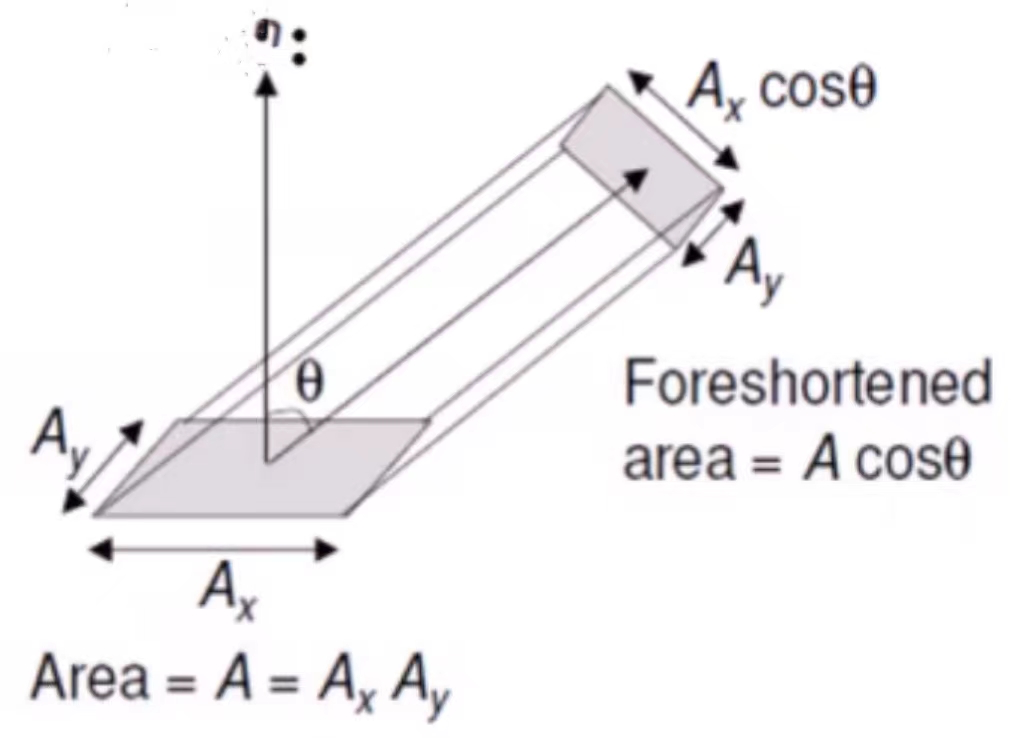
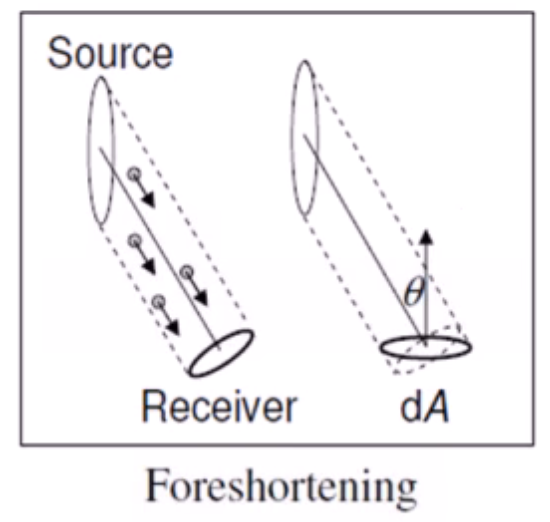
• 投影面积(Foreshortened Area)

1. 投影面积描述了一个物体表面的微小区域在某个视线方向上的可见面积。
2. 对于面积微元A，则沿着与法向夹角为θ方向的A的可见面积为：

Area = Acosθ

• 光能(Radiant Energy)

1. 光能表示的是(一个区域中)光子能量的总和。
2. 光能通常使用符号Q来表示，其单位是焦耳(J)。

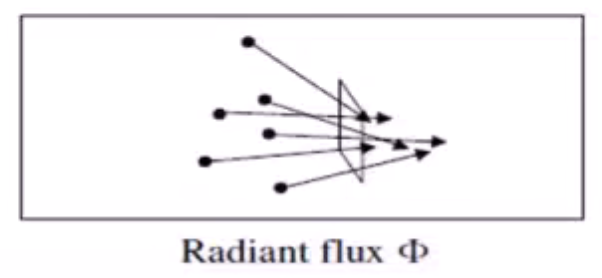
• 光通量(Radiant Flux)

1. 光能并不会停留和储存在某个位置，而是在始终不断运动着的。
2. 光通量描述的是在单位时间穿过单位面积截面的光能：

Φ = \(dQ \over dt\)

通常使用符号Φ来表示，单位是瓦特(W)。

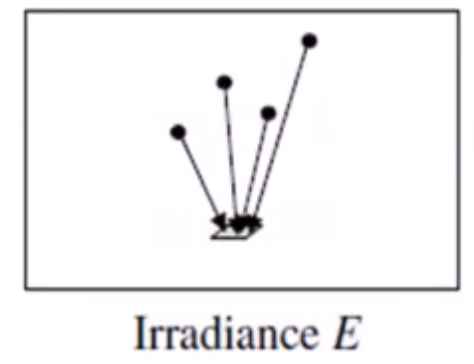
• 辉度(Irradiance)

辉度表示的是物体表面受光能的影响程度，它等于单位面积上的光通量：

E = \(dΦ \over dA\)

通常使用符号E来表示，单位是W/\(m^2\)。

• 发光强度(Intensity)

对一个点(例如点光源)来说，发光强度表示单位立体角上的光通量：

I = \(dΦ \over dω\)

发光强度简称光强，使用符号I来表示，单位是W。

• 光亮度(Radiance)

光亮度表示物体表面沿某一方向的明亮程度，它等于单位投影面积和单位立体角上的光通量，使用I(L?)来表示，单位是W/\(m^2\)

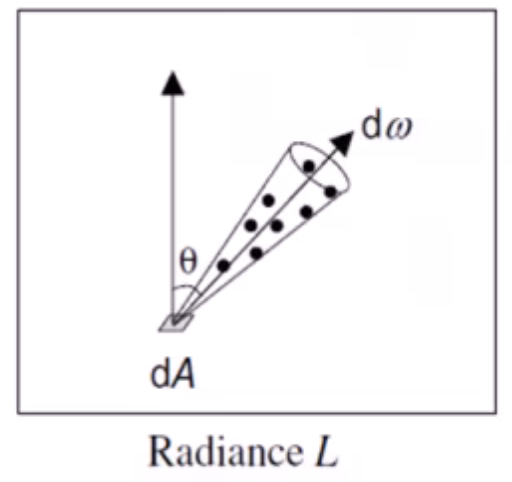
一种直观的光亮度的理解方法是：将光亮度理解为物体表面的微面元所接收的来自于某方向光源的单位面积的光通量，因此截面选用垂直于该方向的截面，其面积按投影面积计算。

光亮度的微分形式：

L = \(d^2Φ \over dAcosθdω\)

光亮度使用物体表面沿目标方向上的投影面积而不是面积。

• 辉度与光亮度的关系

辉度可以写成光亮度在入射光所形成的半球上的积分：

\(dΦ \over dA\) = E = \(\int_ΩL(ω)cosθdω\)

1. Ω是入射光所形成的半球。
2. L(ω)是沿ω方向的光亮度。

BRDF的定义与性质

• BRDF的定义

1. BRDF描述的是物体表面将光能从任何一个入射方向反射到任何一个视点方向的反射特性。
2. BRDF模型是绝大多数近代图形学算法中用于描述光反射现象的基本模型。
3. BRDF是关于入射光方向和反射光方向的四维实值函数，它等于反射方向的光亮度和沿入射方向的入射光的辉度之比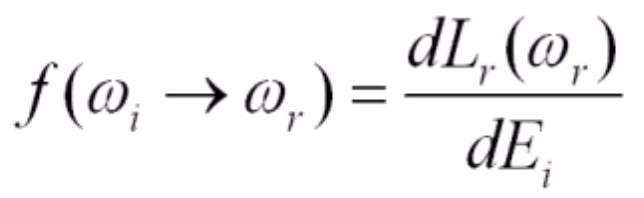：，这里\(ω_i\)是入射光的立体角，\(ω_r\)是反射光的立体角。\(dL_r(ω_r)\)是反射光的光亮度，\(dE_i\)是入射光的辉度。
   1. 可以写成关于入射光的光亮度的形式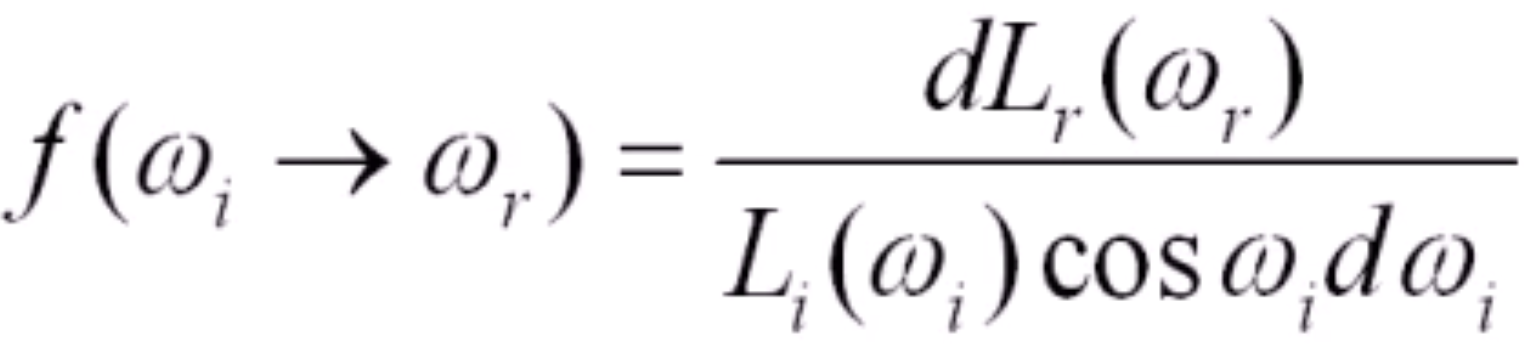：，这里是根据辉度跟光亮度的关系，这样的话分子、分母都是光亮度，原本\(E_i\)是积分，则\(dE_i\)会将积分符号去掉，变成微分形式。

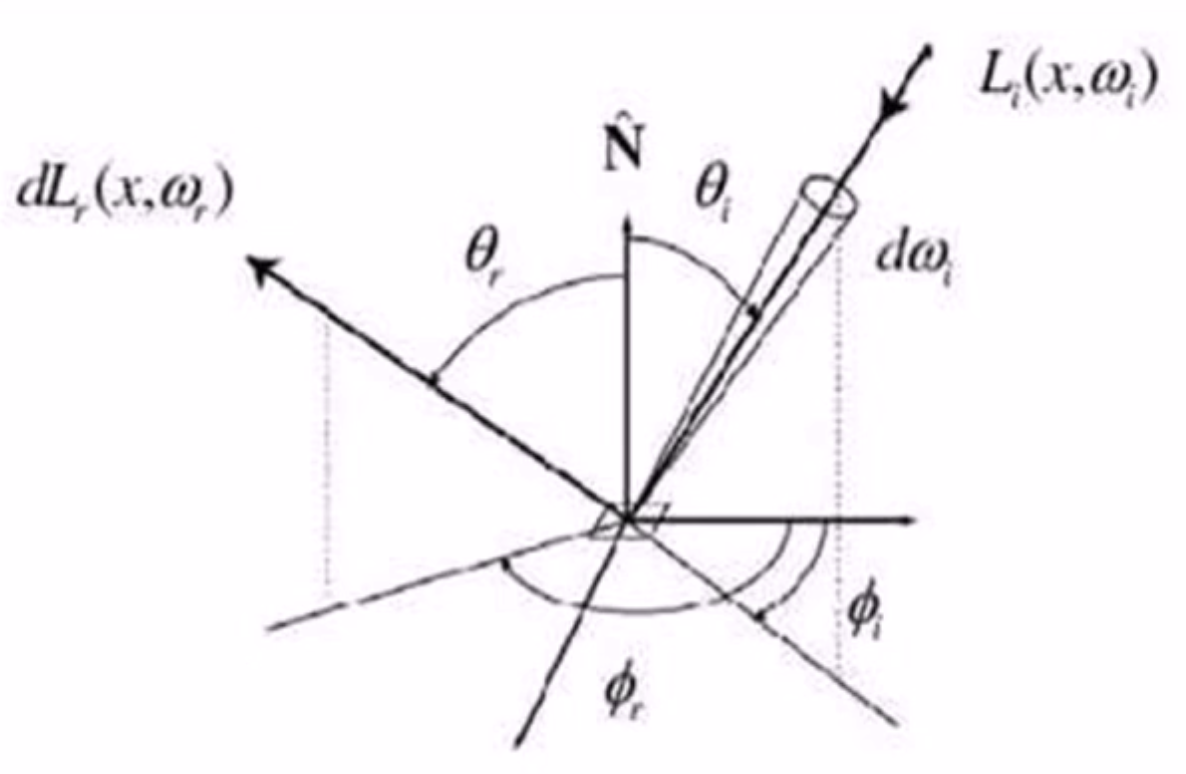
在上图中，右边的箭头是入射光，左边的箭头是反射光，假设我们的人眼在反射方向上，那么人眼看到的东西跟反射光的光强、光亮度有关系。不同方向的光照到图中的一点都可能会到反射方向上来，所以在考虑入射的时候需要考虑面积的积分，则入射的时候需要辉度。即不同方向的光都会对人眼产生影响。这里我们可以看到入射光和反射光在这里并不是关于法向N对称的。

• BRDF的可逆性

1. BRDF的可逆性源自于Helmholtz光路可逆性(Helmholtz Reciprocity Rule)。
2. BRDF的可逆性是说：交换入射光与反射光的角色，并不会改变BRDF的值。

• 能量守恒性质

1. BRDF需要遵循的另一个物理定律是能量守恒定律。能量守恒定律指出：入射光的能量与出射光的总能量应该相等。
2. 能量守恒方程如下：
   1. 
   2. 这里\(Q_{incoming}\)为入射光能量，\(Q_{reflected}\)为反射光能量，\(Q_{absorb}\)为吸收的能量，\(Q_{transmitted}\)为透射(折射)的能量。
3. 由此我们知道：
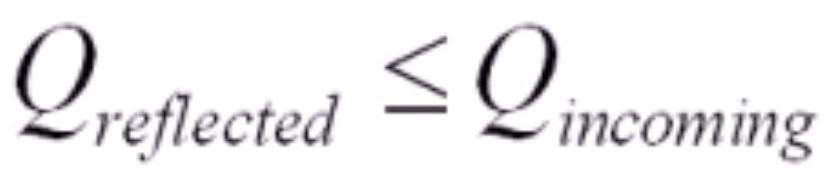   1. 反射光能量一定小于等于入射光能量。
4. 因此BRDF必须满足如下的积分不等式，也就是所谓的能量守恒性质：
   1. 

• 渲染方程(Rendering Equation)

渲染方程用于计算环境光照明下的反射光的光亮度，它可以写成不同角度下反射光的光亮度乘以BRDF的积分：

{{o.name}}

{{m.name}}