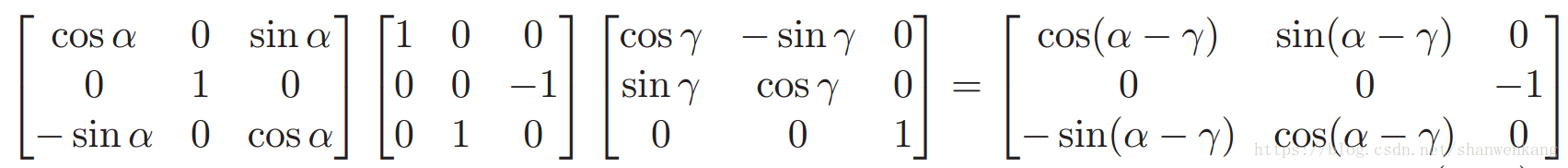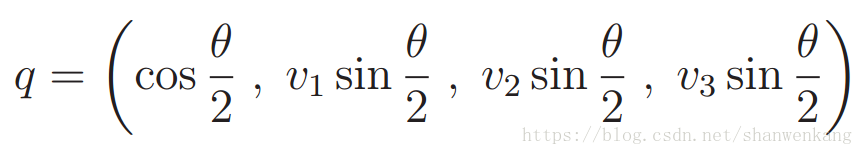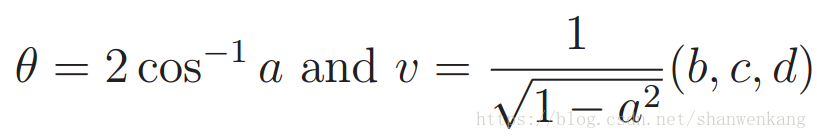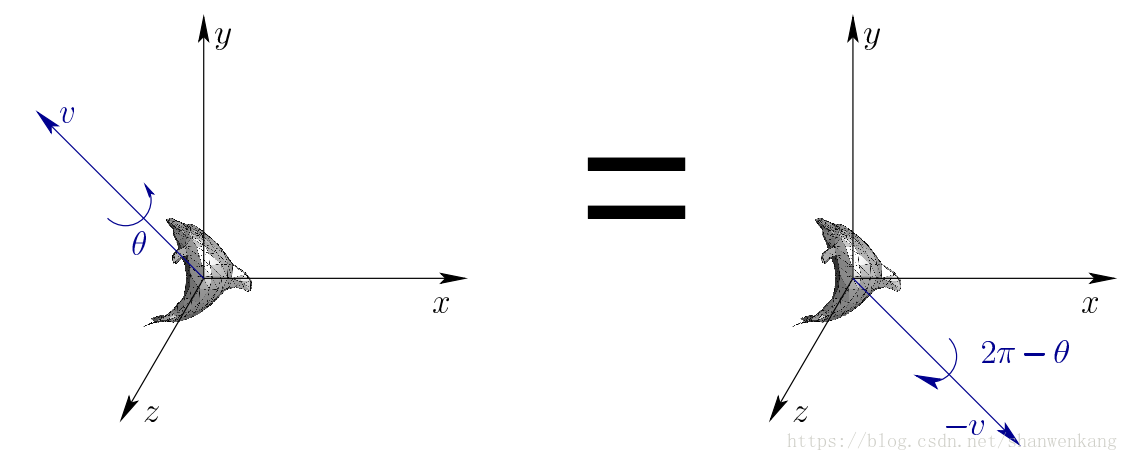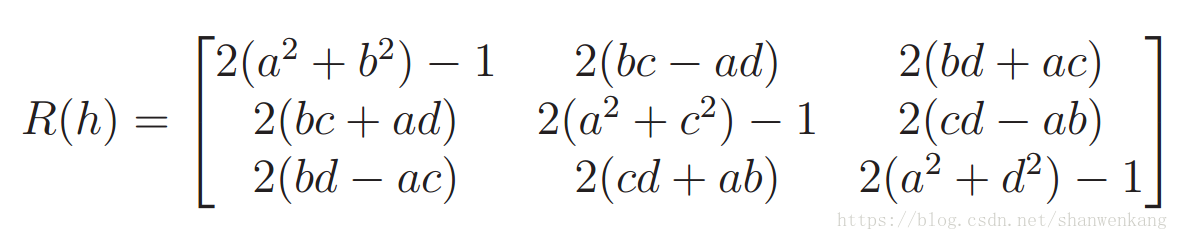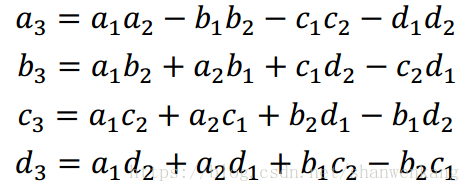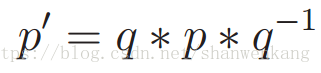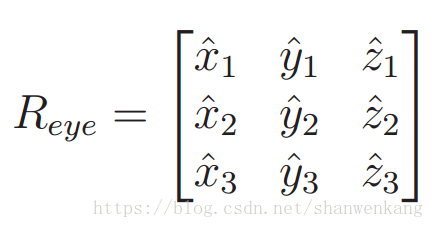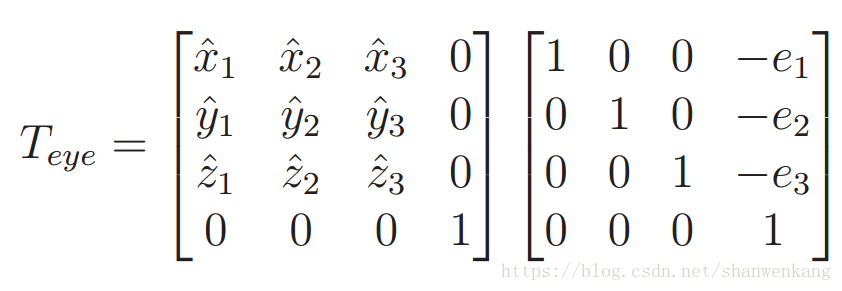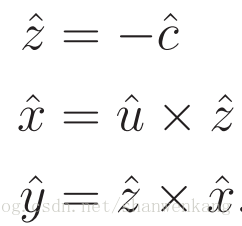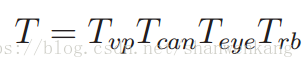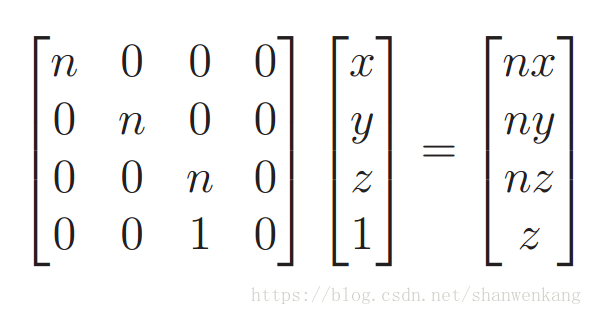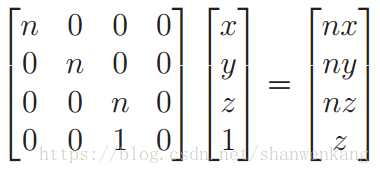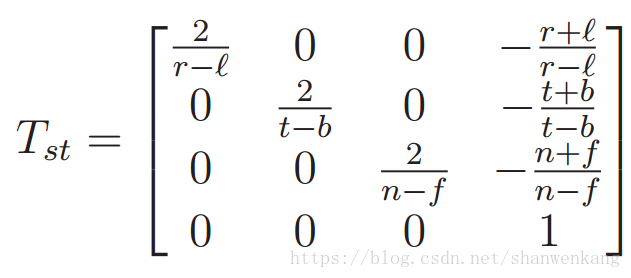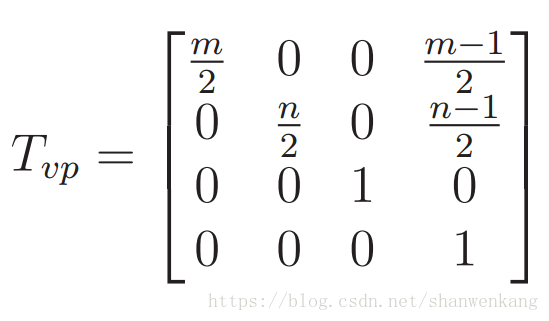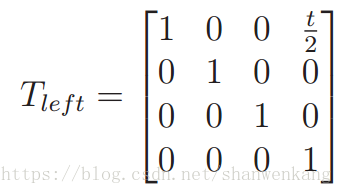Part I
Part II
四元数
如上节所说的欧拉旋转是很复杂的，原因有三：（1）参数化的过程不简单，仅由 3 个独立的参数来代替旋转矩阵中 9 个元素（2）每次的旋转轴是不同的。（3）运算是不可交换的，所以顺序非常重要。更加重要的是用这种方法表示旋转会出现万向节死锁的情况，我之前也写过一篇关于万向节死锁的理解，有兴趣可以看一下（戳我）。从矩阵的角度看是如下情况（俯仰角β=π/2）
上式第二个矩阵对应着俯仰角β = π/2（3.17）。经过矩阵乘法和减法三角恒等式，我们得到右面的结果。可以发现，矩阵中的元素是一个关于α 和 γ的函数，但是仅有α 和 γ的差对结果有影响，所以它只有一个自由度。
这个问题用轴‐角表示方法可以轻易的解决，这推动了一个新的数学概念的产生叫做四元数。四元数 h 是一个 4D 的向量：q=(a,b,c,d)，a,b,c,d 均取实数。因此， q 可以认为是 4 维空间的一个点。经过证明，我们仅能用单位四元数来表示 3D 旋转，也就是说要保证a^2+b^2+c^2+d^2=1。可以看出， 这是一个在单位球面上的方程， 只是维度要更高一些。 通常的球面是一个 2D
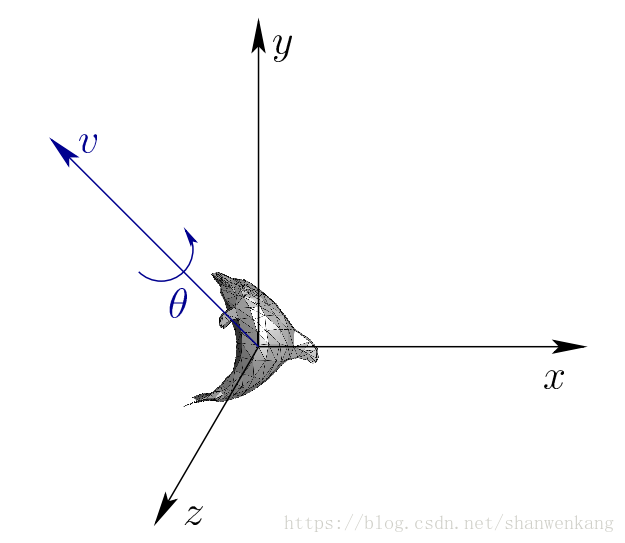
平面，而单位四元数是在一个 3D 的“超平面”上，通常也叫做流形。令（v， θ）为 3D 旋转的轴‐角并表示，如下图所示。它可以转化为下面的四元数形式：
将 q 考虑成一个表示 3D 旋转的数据结构，同样的，也可以将 q 转换为（v， θ）
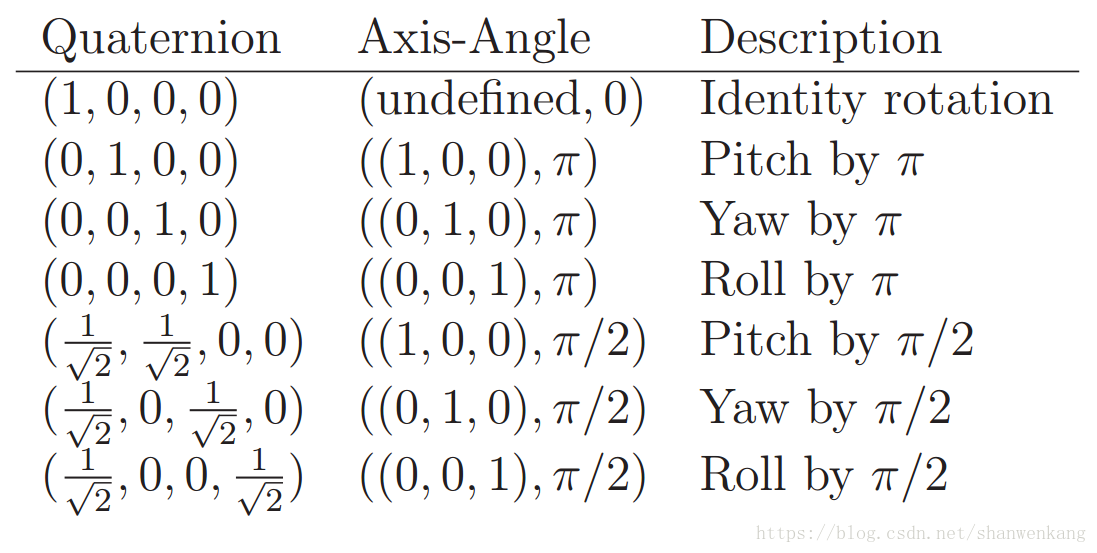
如果 a=1，那么上式不成立，这也正对应了恒等旋转的情况（旋转角度为0），下图展示了几个常见的例子：
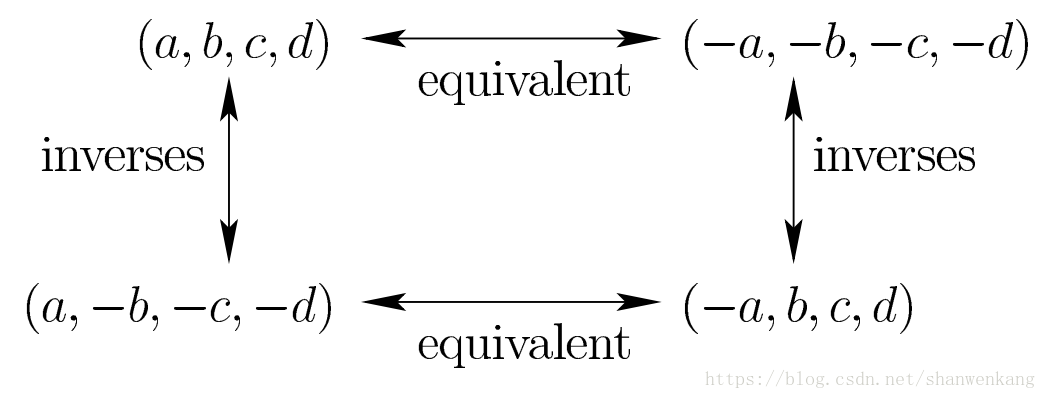
下图展示了四元数及其对应旋转之间的关系
水平箭头的 q 和‐q 表示相同的旋转， 对应着下图中的两种表示方式； 从四元数的表达式中也可以看出它们之间的相等关系。竖直箭头对应着反向旋转，是因为轴的方向反向了（旋转θ变成了旋转 2π‐θ）。
另外，我们可以将四元数表达为旋转矩阵的形式
更方便的是，我们定义四元数乘法， 对于任意两个四元数 q1 和 q2， 乘积用 q1*q2表示，定义如下：
我们使用关于 h 的旋转表达式来对（x， y， z）点进行旋转。令 p=（x， y， z， 1），这是为了给点 p 与四元数相同的维数。通过应用四元数乘法来旋转这个点，如下式所示：
其中 q-1 =（a， -b， -c， -d）（从四元数对照关系的式子中可以得到）。 旋转后的点是（x'， y'， z'），它取自结果 p'=（x'， y'， z'， 1）。
视角变换
本节介绍如何转换虚拟世界中的模型，以便它们出现在虚拟屏幕上。
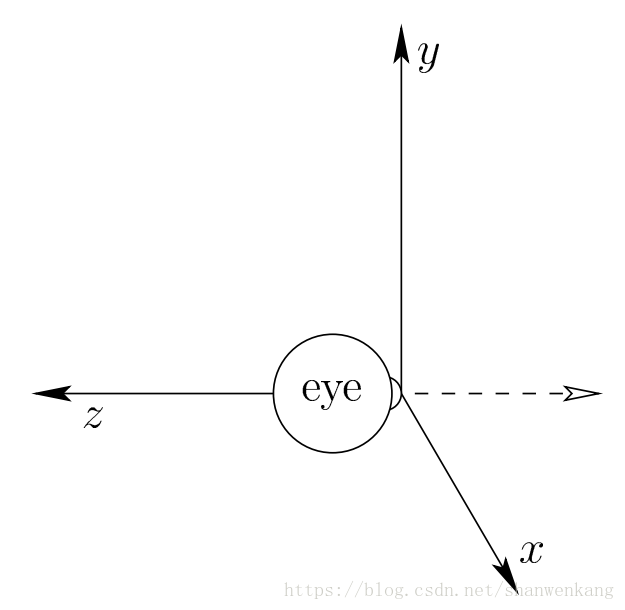
下图显示了一个俯视负 Z 轴的虚拟眼睛。它的放置位置从眼睛的角度来看， x 向右增加， y 向上，这对应于一般的笛卡尔坐标。
如果我们把眼球看做一个放置在三维世界的物体，它的位置在e = (e1, e2, e3)，旋转由如下矩阵给出：
那么为了显示三维世界中其他的物体，我们需要将虚拟世界中的所有模型移动到眼睛的参照系，这意味着我们需要应用逆变换：
为了渲染眼睛看到的图像，我们首先需要对眼球的朝向进行建模，我们需要用以下三个特征描述它：
1.眼睛的位置： e
2.眼睛的中心方向：ˆ c
3.向上的方向：ˆ u
ˆ c与 ˆ u都是单位向量。或眼睛的向上方向。
我们现在需要从上述条件构造Teye。平移部分已经由 e 来确定，我们只需要确定旋转 Reye，Reye的每个列向量计算为
正交投影
当 Teye 已知，设（x， y， z）表示任意点的坐标。如果我们强制把每个 z 坐标取值为 0，然后将所有点直接投影到垂直 xy 平面中，将会发生什么？换句话说，也就是（x， y， z）→（x， y， 0），这就是所谓的正交投影。这会带来以下几个问题：
1.混杂的物体将被叠加，而不是物体之间有相互遮挡的关系。
2.显示画面将在所有方向无限延伸（z 除外）。但实际情况是，如果显示器是 xy 平面上的一个小矩形，则超出范围的模型部分可以被消除掉。
3.不满足距离较近的物体应大于距离较远的物体。
前两个问题是图形学中的重要问题，我们将在以后介绍，下面主要解决一下第三个问题。
透视投影
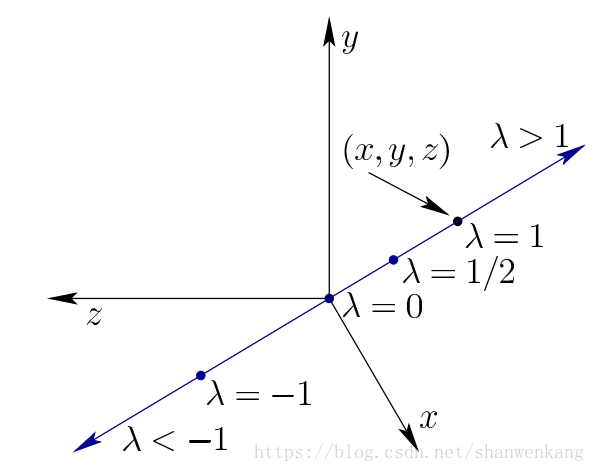
我们定义一个透视投影，而不用上述提到的正交投影。 对于每个点（x， y， z）它位于通过原点的一条线上。 下式表示直线中所有点的集合：（λx，λy，λz）。其中λ可以是任何实数。 换句话说，λ是一个能够到达线上所有点（包含（x， y， z）和（0， 0， 0））的参数
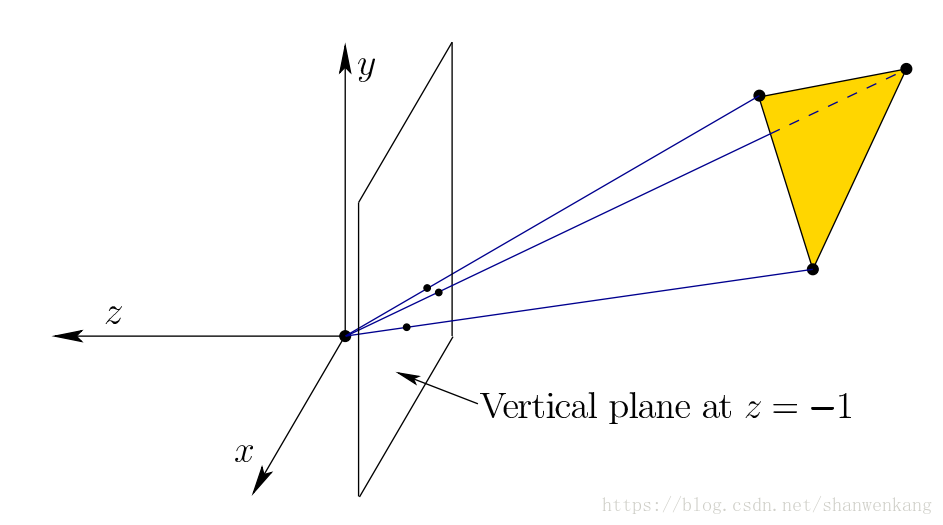
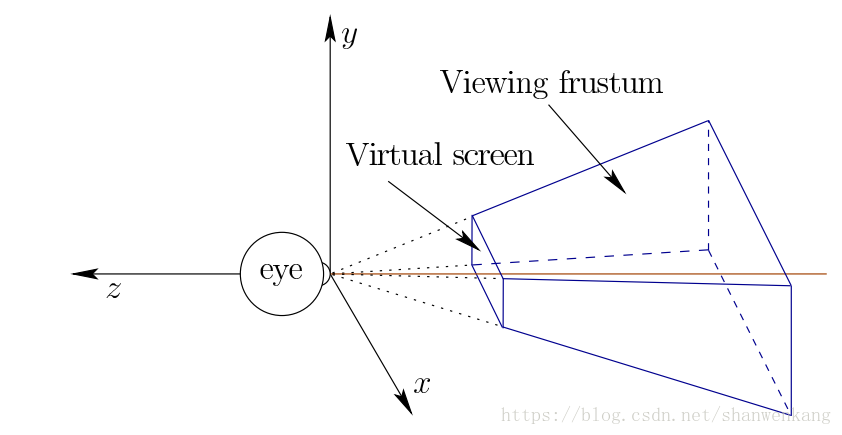
现在我们可以在虚拟世界的任何地方放置一个“电影屏幕”，并查看所有线条穿透它的位置。 为了简单化这个数学表达式，我们选择 z = -1 平面将我们的虚拟屏幕直接放在眼睛的前方，见下图。我们有λz= -1，这意味着λ= -1 / z。屏幕上点的坐标计算为 x'= -x / z， y'= -y / z。 请注意，由于 x和 y 对于每个轴的缩放量 z 相同，因此它们的宽高比将保留在屏幕上。
更一般地说，假设垂直屏幕放置在沿着 z 轴的某个位置 d 处。 在这种情况下，我们可以获得更多的通用表达式来显示屏幕上某个点的位置：x′ = dx/z ， y′ = dy/z。以上就是我们将点投影到虚拟屏幕上， 同时考虑到各种距离下物体的缩放属性时所需要做
的所有事情。
转换级联
通过将以上提到的所有变换级联在一起，同时稍微调整其形式以适应 VR 和计算机图形工业目前使用的形式，我们就可以将三维世界中的物体转换到我们的显示屏幕上了。该级联的一般表达式如下：
当 T 应用于点（x， y， z， 1）时，会生成屏幕上点的位置。请记住，这些矩阵乘法不可交换，并且操作顺序是从右向左。第一个矩阵 Trb 是应用于可移动模型上的点的刚体变换。对于三维世界中不同的刚体，对应的Trb不同。在应用 Trb 之后， Teye 将虚拟世界转换为眼睛的坐标系。
规范化视图变换
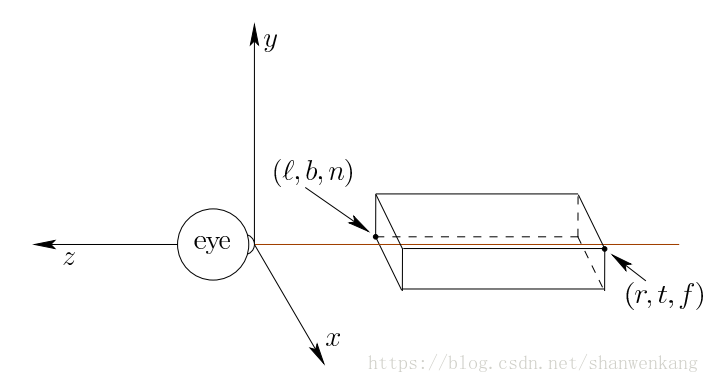
下一个变换， Tcan 执行之前提到的透视投影，我们希望变换的结果是一种看起来没有单位的规范形式，因此， Tcan 被称为规范视图变换，下图显示了一个的四个角的视锥，透视投影应该将截锥内的所有点放置在以近平面为中心的虚拟屏幕上。 z = n 和 z = f 分别为近平面和远平面。请注意，这些情况下 z <0，因为 z 轴指向相反的方向，虚拟屏幕为近平面。
我们可以修改透视投影的表达式 x′ = dx/z ， y′ = dy/z 来适应这种情况：
在前两个坐标中，我们得到表达式的分子。 表达式的非线性分母是 1 / z 因子。 为了处理这个问题，第四个坐标用来表示 z，而不是 1，以此来处理 Trb。所得到的 4D 矢量被解释为一个 3D 矢量， 该矢量通过划分其第四个分量来缩放。 例如，（v1，v2， v3， v4）被解释为（v1/v4，v2/v4， v3/v4），因此上述结果被解释为（nx/z , ny/z , n）
跟踪深度
以下矩阵常用于计算机图形学：
除了转换 z 坐标外，这个矩阵与上面提到的矩阵相同。在这个矩阵中，z坐标有另一个作用：跟踪每个点与眼睛的距离， 以便图形算法可以确定对象的前后关系。矩阵 Tp 计算第三个坐标为：(n + f)z - fn 。当这个式子除以 z以后，原来的距离将不会被保留，而是保留了物体的相对关系。例如，如果点 p 比点 q 离眼睛更远，那么通过上式计算以后，二者的距离可能发生改变，但是却一直能保证点p比点q远。此外，它确实保留了两种特殊情况下的距离： z = n 和 z = f ，在这两个面上，变换前与变换后点的z坐标相同。
额外的转换和缩放
用 Tp 后，视锥的 8 个角被转换成矩形框的角，如下图 所示。
以下变换对z 轴进行了一个简单的转换，并进行了一些重新调整，使其在原点处居中，其角点坐标为（±1，±1，±1）：
最后，我们将规范视图变换 Tcan 定义为：Tcan = Tst · Tp
视角变换
在级联表达式中应用的最后一个转换是视角变换Tvp。 在应用了 Tcan 之后， x 和 y坐标的范围是从-1 到 1。 需要最后一个步骤才能将投影点带到用于对物理显示中的像素进行索引的坐标。令 m 为水平像素的数量， n 为垂直像素的数量。 例如，对于 1080p显示器， n = 1080， m = 1920。 那么显示索引的行数从 0 到 n-1，列数从 0 到 m-1。此外，（0， 0）位于左下角。在这种情况下，视角变换是
左右眼
在级联表达式中求出的Teye实际上是一个等效的视点，代表的是两眼的中点，因此我们需要将这个变换矩阵推广到左右眼的情况。设 t 表示左右眼之间的距离。其在现实世界中的值因人而异，其平均值在 t = 0.064 米左右。为了处理左眼视图，我们需要简单地将等效的视点水平向左移动即可。
当从眼睛的角度看时，这对应于模型的右移。这个转换放在 Teye 之后再来调整它的输出。因此：
右眼是与上述相反的情况。
以上就是在虚拟世界中放置和移动模型的整个转换公式。应用了它以后，我们就能实现从虚拟世界到视角窗口的映射了，当然这只是最简单的情况，实际上我们还需要对它进行其他的变换以补偿由于 VR 头戴式设备中的广角镜头而导致的非线性光学失真。