SVM(Support Vector Machine)-1-linear

SVM(Support Vector Machine)-1-linear

综述

这一节纯理论,前方贼高能!!!!
在算法实现的角度上来说,我们需要先感性认识这个算法怎么work的

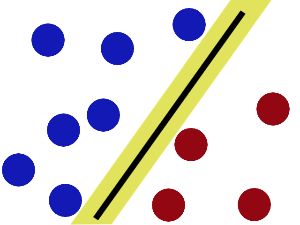
很直接地,向量机就是在找一条可以把在同一个空间的两样东西分开的线,数学一点的图:
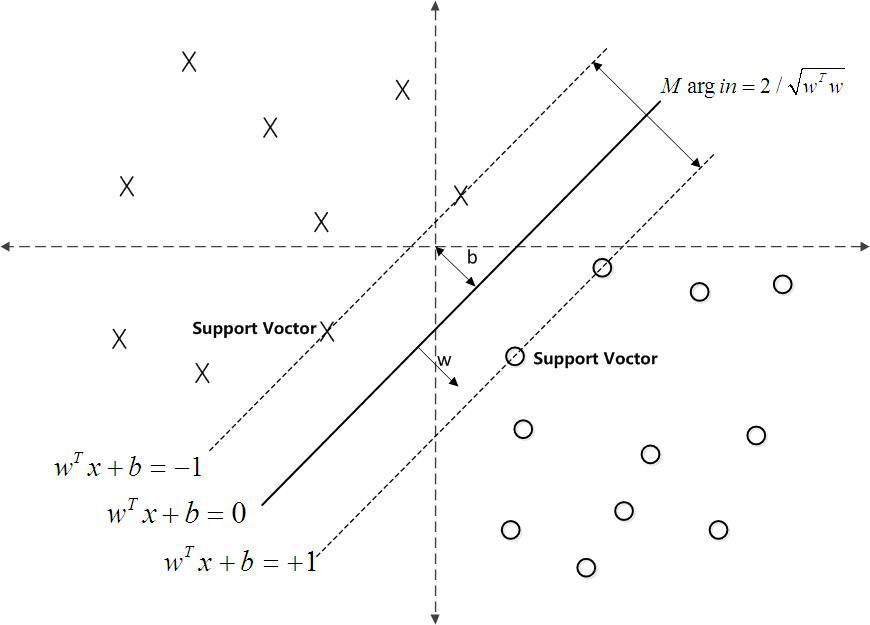
show2
所有不懂的数学符号和定义,在文末都有blog说明

线性可分支持向量机

由上面的讨论,有定义:

超平面

ω^{T} x + b = 0

$\omega^T x+b=0$
相应的 分类决策函数是:

y = f (x) = s i g n (ω^{T} ∙ x + b = 0)

$y=f(x)=sign(\omega^T \bullet x+b=0 )$
取转置这一点就可以知道,

ω

$\omega$ 定义的是这条线的法向量.由高数的知识可知道.在法向量定义下,可以确定一个高一维的平面(特征)

为了方便理解,我会一直用线这个名词代替 超平面这个名词,但是千万不要简单地以为向量机的维度就是一二维的!

同时可以带来后面定义的便利:

函数间隔和几何间隔

当线 $f(x)=sign(\omega^T \bullet x+b=0 )$ 确定的时候,每一个点对线的距离为:

r = ω ∙ x_{i} + b

$r=\omega\bullet x_i+b$
在这个基础上,加上我们的分类决策函数的结果:

{\hat{γ}}_{i} = y (w^{T} x + b)

$\widehat{\gamma}_i = y(w^Tx + b)$

\hat{γ}

$\widehat{\gamma}$ 被称为 函数间隔(functional margin)
这样做有两个好处:
1. 可以从符号看到分类的正确性
2. 可以从大小看到分类的 确信度

定义关于训练数据集T的超平面的函数间隔为:T中所有样本点的函数间隔最小值:

\hat{γ} = min_{i = 1, . . ., N} {\hat{γ}}_{i}

$\widehat{\gamma} =\min \limits_{i=1,...,N} \widehat{\gamma}_i$
为什么这样定义的话,后面讲到 支持向量的时候会讲到.
由于

ω

$\omega$ 和

b

$b$ 在同时扩大或缩小时,会让

γ

$\gamma$ 线性改变

所以,通过 归一化处理之后,可以得到:
几何间隔(geometrical margin)

γ_{i} = \frac{{\hat{γ}}_{i}}{| | ω | |}

$\gamma_i=\frac{\widehat{\gamma}_i}{||\omega||}$
同理:定义关于训练数据集T的超平面的几何间隔为:T中所有样本点的几何间隔最小值:

γ = \frac{\hat{γ}}{| | ω | |}

$\gamma=\frac{\widehat{\gamma}}{||\omega||}$
显式表达是:

γ_{i} = y_{i} (\frac{ω}{| | ω | |} ∙ x_{i} + \frac{b}{| | ω | |})

$\gamma_i= y_i \big (\frac{\omega}{||\omega||} \bullet x_i+\frac{b}{||\omega||} \big )$

扫描二维码关注公众号，回复： 3083347 查看本文章

归一化之后,这个间隔指的才是直观意义上点到线的距离
定义这两个东西的一个很直观的意义是为了定义损失函数,此处省略,好好想想吧

最大间隔分类器

看图上的两条虚线(Gap),他存在的意义就在于,当我的Gap越大,就证明我这条线和dataset的距离越远。
这样分类的效果就会越好，因为换个角度说，每一个分类的值域就会被这条线和间隔限制得越来越小。
可以用数电的噪声容限这个概念来帮助理解一下.

明显这是个几何参量定义，所以用几何间隔定义下，有最大间隔分离超平面：

max_{ω, b} γ

$\max \limits_{\omega , b} \gamma$

s . t . γ_{i} = y_{i} (\frac{ω}{| | ω | |} ∙ x_{i} + \frac{b}{| | ω | |}) \geq γ

$s.t. \quad \gamma_i= y_i \big (\frac{\omega}{||\omega||} \bullet x_i+\frac{b}{||\omega||} \big ) \ge \gamma$

最大间隔分离超平面具有存在唯一性,此处不作证明

显然,这里换成函数间隔来往下走是更好的选择:

max_{ω, b} \frac{\hat{γ}}{| | ω | |}

$\max \limits_{\omega , b}\frac { \widehat{\gamma}}{||\omega||}$

s . t . γ_{i} = y_{i} (ω ∙ x_{i} + b) \geq \hat{γ}

$s.t. \quad \gamma_i= y_i \big ( \omega \bullet x_i+{b}\big ) \ge \widehat{\gamma}$
因为前面讲过函数间隔拥有线性变化的性质,可以知道函数间隔并不会影响上面公式的解,所以不妨令

\hat{γ} = 1

$\widehat{\gamma}=1$

这种做法称为硬间隔最大化,指的是gap的不可变性

为了后续的公式化简,最大值也作了一点trick:

\begin{matrix} (1.1) & min_{ω, b} \frac{1}{2} | | ω | |^{2} \end{matrix}

$\min\limits_{\omega , b} \frac12 ||\omega||^2 \tag{1.1}$

\begin{matrix} (1.2) & s . t . y_{i} (ω ∙ x_{i} + b) - 1 \geq 0 \end{matrix}

$s.t. \quad y_i \big ( \omega \bullet x_i+{b}\big ) -1 \ge 0 \tag{1.2}$
从数学的角度上,这是一个凸二次(w,b)规划(convex quadratic programming)问题

支持向量和间隔边界

显然,在训练完之后,这条线是不是只会和线(或Gap)上的点有关系,所以就称满足
- $\quad y_i \big ( \omega \bullet x_i+{b}\big ) -1 = 0$ 的数据称为支持向量(Support Vector)

所以SVM的中文读法是支持向量 $\quad$ 机,而不是支持 $\quad$ 向量机 ,重点!!!

两条虚线之间的距离称为间隔(margin),虚线称为间隔边界
- gap= $\frac2{||\omega||}$

work it out (linear)

回到凸二次(w,b)规划(convex quadratic programming)问题,显然,从高数我们就可以知道,在这种情况下,我们应该引入

拉格朗日算子

在单不等式约束中:

L (x, y, λ) = f (x, y) + λ ∙ (g (x, y) - c)

$\mathcal{L}(x,y,\lambda) = f(x,y) + \lambda\bullet(g(x,y)-c)$
显然,在k项不等式约束中:

L (x, y, λ_{1}, . . ., λ_{k}) = f (x, y) - \sum_{i - 1}^{k} λ_{i} g_{i} (x, y)

$\mathcal{L}(x,y,\lambda_1,...,\lambda_k) = f(x,y) - \sum_{i-1}^k\lambda_i g_i(x,y)$
求解可以参考高数书一(下),9.45.46

其中,f为原函数,g为约束函数. $\lambda 为拉格朗日算子$

故代入(1.1)和(1.2)得:

L (w, b, α) = \frac{1}{2} | | w | |_{2}^{2} - \sum_{i = 1}^{k} α_{i} [y_{i} (w^{T} x_{i} + b) - 1], α_{i} \geq 0

$\mathcal{L}(w,b,\alpha) = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{k}\alpha_i[y_i(w^Tx_i + b) - 1] \; \quad ,\alpha_i \geq 0$

L (w, b, α) = \frac{1}{2} | | w | |_{2}^{2} - \sum_{i = 1}^{k} α_{i} y_{i} (w^{T} x_{i} + b) + \sum_{i = 1}^{k} a_{i}, α_{i} \geq 0

$\mathcal{L}(w,b,\alpha) = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{k}\alpha_i y_i(w^Tx_i + b) +\sum_{i=1}^k a_i\; \quad ,\alpha_i \geq 0$

在规划有解的前提下,由拉格朗日对称性,函数的优化可以转化为极大极小问题:

ψ (a) = \underset{α_{i} \geq 0}{\underset{⏟}{m a x}} \underset{w, b}{\underset{⏟}{m i n}} L (w, b, α)

$\psi(a)=\underbrace{max}_{\alpha_i \geq 0} \;\underbrace{min}_{w,b}\; \mathcal{L}(w,b,\alpha)$

推导:

(1) $\underbrace{min}_{w,b}\; \mathcal{L}(w,b,\alpha)$

由于要求最小值,变量为w,b,不妨分别对他们求偏导并置零:

\frac{\partial L}{\partial ω} = 0 \Rightarrow ω = \sum_{i = 1}^{k} α_{i} y_{i} x_{i}

$\frac{\partial \mathcal{L}}{\partial \omega} = 0 \;\Rightarrow \omega = \sum\limits_{i=1}^{k}\alpha_iy_ix_i$

\frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i = 1}^{k} α_{i} y_{i} = 0

$\frac{\partial \mathcal{L}}{\partial b} = 0 \;\Rightarrow \sum\limits_{i=1}^{k}\alpha_iy_i = 0$
版本一(抄来的):

\begin{aligned} (1) & ψ (α) & = \frac{1}{2} | | w | |_{2}^{2} - \sum_{i = 1}^{m} α_{i} [y_{i} (w^{T} x_{i} + b) - 1] \\ (2) & = \frac{1}{2} w^{T} w - \sum_{i = 1}^{m} α_{i} y_{i} w^{T} x_{i} - \sum_{i = 1}^{m} α_{i} y_{i} b + \sum_{i = 1}^{m} α_{i} \\ (3) & = \frac{1}{2} w^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - \sum_{i = 1}^{m} α_{i} y_{i} w^{T} x_{i} - \sum_{i = 1}^{m} α_{i} y_{i} b + \sum_{i = 1}^{m} α_{i} \\ (4) & = \frac{1}{2} w^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - w^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - \sum_{i = 1}^{m} α_{i} y_{i} b + \sum_{i = 1}^{m} α_{i} \\ (5) & = - \frac{1}{2} w^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - \sum_{i = 1}^{m} α_{i} y_{i} b + \sum_{i = 1}^{m} α_{i} \\ (6) & = - \frac{1}{2} w^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - b \sum_{i = 1}^{m} α_{i} y_{i} + \sum_{i = 1}^{m} α_{i} \\ (7) & = - \frac{1}{2} (\sum_{i = 1}^{m} α_{i} y_{i} x_{i})^{T} (\sum_{i = 1}^{m} α_{i} y_{i} x_{i}) - b \sum_{i = 1}^{m} α_{i} y_{i} + \sum_{i = 1}^{m} α_{i} \\ (8) & = - \frac{1}{2} \sum_{i = 1}^{m} α_{i} y_{i} x_{i}^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} - b \sum_{i = 1}^{m} α_{i} y_{i} + \sum_{i = 1}^{m} α_{i} \\ (9) & = - \frac{1}{2} \sum_{i = 1}^{m} α_{i} y_{i} x_{i}^{T} \sum_{i = 1}^{m} α_{i} y_{i} x_{i} + \sum_{i = 1}^{m} α_{i} \\ (10) & = - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} y_{i} x_{i}^{T} α_{j} y_{j} x_{j} + \sum_{i = 1}^{m} α_{i} \\ (11) & = \sum_{i = 1}^{m} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{m} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{aligned}

$\begin{align} \psi(\alpha) & = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \\& = \frac{1}{2}w^Tw-\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i -\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}(\sum\limits_{i=1}^{m}\alpha_iy_ix_i)^T(\sum\limits_{i=1}^{m}\alpha_iy_ix_i) - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i + \sum\limits_{i=1}^{m}\alpha_i \\& = -\frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_iy_ix_i^T\alpha_jy_jx_j + \sum\limits_{i=1}^{m}\alpha_i \\& = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \end{align}$

版本二:
由于意识到对单个 $y_i,a_i$ 来说,他们都只是一个实数而已,所以,他们的矩阵的转置等于他们本身:

\begin{aligned} ψ (α) & = \frac{1}{2} | | w | |_{2}^{2} - \sum_{i = 1}^{N} α_{i} [y_{i} (w^{T} x_{i} + b) - 1] \\ = \frac{1}{2} ω^{T} ω - \sum_{i = 1}^{N} α_{i} y_{i} (w^{T} x_{i} + b) + \sum_{i = 1}^{N} a_{i} \\ = - \frac{1}{2} \sum_{i = 1, j = 1}^{N} α_{i} y_{i} α_{j} y_{j} (x_{i}^{T} ∙ x_{j}) - \sum_{i - 1}^{N} a_{i} y_{i} ((\sum_{j = 1}^{N} a_{j} y_{j} x_{j}) ∙ x_{i} + b) + \sum_{i = 1}^{N} α_{i} \\ = \sum_{i = 1}^{N} α_{i} - \frac{1}{2} \sum_{i = 1, j = 1}^{N} α_{i} α_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{aligned}

$\begin{align*} \psi(\alpha) & = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{N}\alpha_i[y_i(w^Tx_i + b) - 1]\\&= \frac{1}{2}\omega^T \omega - \sum\limits_{i=1}^{N}\alpha_i y_i(w^Tx_i + b) +\sum_{i=1}^N a_i \\ & = -\frac{1}{2}\sum\limits_{i=1,j=1}^{N}\alpha_iy_i \alpha_jy_j(x_i^T\bullet x_j) -\sum_{i-1}^N a_iy_i\Big( \big( \sum_{j=1}^N a_j y_j x_j \big)\bullet x_i +b\Big) + \sum\limits_{i=1}^{N}\alpha_i \\ & = \sum\limits_{i=1}^{N}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{N}\alpha_i\alpha_jy_iy_jx_i^Tx_j \end{align*}$

(2)对 $psi(a)=\underbrace{max}_{\alpha_i \geq 0} \;\underbrace{min}_{w,b}\; \mathcal{L}(w,b,\alpha)$ 对a求极大,即是对偶问题
把上面的结果加个负号,可以将a的极大改成极小:

ϕ = \underset{α}{\underset{⏟}{m i n}} \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} ∙ x_{j}) - \sum_{i = 1}^{N} α_{i}

$\phi = \underbrace{min}_{\alpha} \frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \bullet x_j) - \sum\limits_{i=1}^{N} \alpha_i$

s . t . \sum_{i = 1}^{N} a_{i} y_{i} = 0, a_{i} \geq 0

$s.t. \sum_{i=1}^Na_iy_i=0 \quad ,a_i \geq 0$

KKT条件

KKT条件是说最优值必须满足以下条件：

L(a, b, x)对x求导为零；
h(x) =0;
a*g(x) = 0;

KKT的意义是:非线性规划问题能有最优化解法的充分必要条件,主要是因为,很明显,超平面在维度上去之后,显然不是一个线性分类问题,所以要先解决低维向高维转换的可能性

由于篇幅问题,可以参考参考文献的KKT条件-知乎和 extra-3,会有很好的解释

事实证明,用拉格朗日算子可以实现.
由h(x)=0可得(就是要你去翻博客..哼):

a_{i}^{*} (y_{i} (ω^{*} ∙ x_{i} + b^{*}) - 1) = 0

$a_i^*(y_i(\omega^*\bullet x_i+b^*)-1)=0$

result

自此,我们已经就可以得到结果啦:

ω^{*} = \sum_{i = 1}^{N} a_{i}^{*} y_{i} x_{i}

$\omega^*=\sum_{i=1}^N a_i^* y_ix_i$
选择一个正分量

a_{j}^{*} > 0

$a_j^*>0$

b^{*} = y_{j} - \sum_{i = 1}^{N} a_{i}^{*} y_{i} (x_{i} ∙ x_{j})

$b^*=y_j -\sum_{i=1}^N a_i^* y_i(x_i\bullet x_j)$
这样,线性可分支持向量机硬间隔就全部结束了

软间隔

由于上一节说了,我们取了一个 $\widehat{\gamma}=1$ 来简化之后,推出公式就易如反掌了,但是现在我们来考虑一些实际一点的问题:异常点

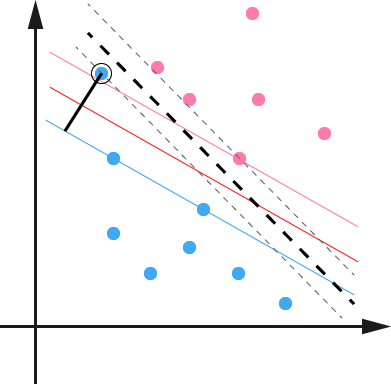
因为在硬间隔中我们就规定了函数间隔是1,面对这种异常点,往往硬间隔在训练的时候是不会自动去除而严重影响结果的.
如图所示,如果不放宽间隔的话,训练出来的结果就是那一条粗虚线,但是如果扩大了间隔之后,可以得到类似红色线这样良好的线

所以这里的重点在于,引入一个松弛变量,放宽间隔:

y_{i} (w ∙ x_{i} + b) \geq 1 - ξ_{i}

$y_i(w\bullet x_i +b) \geq 1- \xi_i$
作为代价,考虑目标函数,

m i n \frac{1}{2} | | w | |_{2}^{2} + C \sum_{i = 1}^{m} ξ_{i}

$min\;\; \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i$
其中,C>0称为惩罚参数,一般是 调参党需要手动给出的参数

work it out

这次其实和上一节的唯一差别就是,拉格朗日算子由两个(w,b)改变到三个(w,b, $\xi$ )
同样的,对L(w,b, $\xi$ )求 $\xi$ 方向的偏导

\frac{\partial L}{\partial ξ} = 0 \Rightarrow C - α_{i} - μ_{i} = 0, μ_{i} > 0

$\frac{\partial L}{\partial \xi} = 0 \;\Rightarrow C- \alpha_i - \mu_i = 0 \quad ,\mu_i>0$
这个限制条件给a_i设置了上限,在明确这点之后,显然,计算出来的结果和上一节是 一摸一样的.
改变在于,限制条件从

a_{i} \geq 0

$a_i \geq 0$ 变成了:

0 \leq a_{i} \leq C

$0\leq a_i\leq C$

边界条件

当 $a_i=C$ 的时候,就证明, $a_i$ 是被 $C- \alpha_i - \mu_i = 0 \quad$ 所限制了。在这个情况下,我们来看看会发生什么:
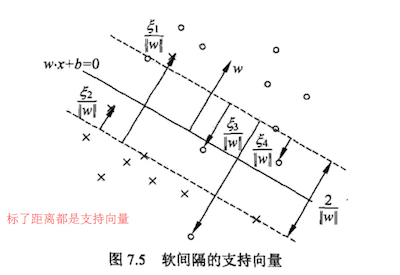
如果α=C，说明这是一个可能比较异常的点，需要检查此时ξi:
- 如果0≤ξi≤1,那么点被正确分类，但是却在超平面和自己类别的支持向量之间。如图中的样本2和4.

如果ξi=1,那么点在分离超平面上，无法被正确分类。
如果ξi>1,那么点在超平面的另一侧，也就是说，这个点不能被正常分类。如图中的样本1和3.

a=c

合页损失函数

　线性支持向量机还有另外一种解释如下：
　

\underset{w, b}{\underset{⏟}{m i n}} [1 - y_{i} (w ∙ x + b)]_{+} + λ | | w | |_{2}^{2}

$\underbrace{ min}_{w, b}[1-y_i(w \bullet x + b)]_{+} + \lambda ||w||_2^2$
　目标函数的第一项

[1 - y_{i} (w ∙ x + b)]_{+}

$[1-y_i(w \bullet x + b)]_{+}$ 称为经验损失或经验风险
　
　其中

L (y (w ∙ x + b)) = [1 - y_{i} (w ∙ x + b)]_{+}

$L(y(w \bullet x + b)) = [1-y_i(w \bullet x + b)]_{+}$ 称为合页损失函数(hinge loss function)，下标+表示为：
　

[z]_{+} = {\begin{cases} z & z > 0 \\ 0 & z \leq 0 \end{cases}

$[z]_{+}= \begin{cases} z & {z >0}\\ 0& {z\leq 0} \end{cases}$

自此线性情况就讲完了.

序列最小最优化算法SMO

这个是用来求解a的,理论来说是现实实现svm最需要的掌握的算法(让求a的速度变快),
但是因为超出了这篇博客的内容,就留到下一篇来写吧
可以在参考文献中看到推荐blog:

https://zhuanlan.zhihu.com/p/29212107

http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988419.html

非线性概述

在线性不可分的时候,我们可以通过核函数将数据映射到核函数对应的特征空间(比如二维转到三维)中.
在特征空间中,使用线性学习器分类
就好像是平面的数据,用某个规则突起其中一些特征数据,然后用一个线性平面去分类,然后将这个线性平面和三维特征空间的交线再投影回原来的平面中
其实说了这么久的核核核,其实就是变换对,功能是特征空间的变换,所以只要符合是正定核,即对称函数的kernel就能被称为一个核
由线性泛函的观点来说,这样的变换可以快速地变换自变量来推出公式:
没变换前:
$f (x) = \sum_{i = 1}^{n} a_{i} y_{i} < x_{i}, x > + b$ $f(x)=\sum^n_{i=1}a_i y_i<x_i,x>+b$
变换后:
$f (x) = \sum_{i = 1}^{n} a_{i} y_{i} < ϕ (x_{i}), ϕ (x) > + b$ $f(x)=\sum^n_{i=1}a_i y_i<\phi (x_i),\phi (x)>+b$
其中:
$\phi(\bullet) 为映射 ,<>为向量内积$

参考文献

理解SVM的三层境界
 范数
 s.t.
拉格朗日乘子
 拉格朗日对偶性
 KKT条件-知乎
 SVM-wiki
sign符号函数
 泛函分析
 非线性分析
 SMO
SMO2
extra-1
extra-2
extra-3
extra-4

《统计学习方法》，李航著；