支持向量机(support vector machine)(SVM)(1)

背景

对于两类问题，给定数据，使用线性函数，如何分类？

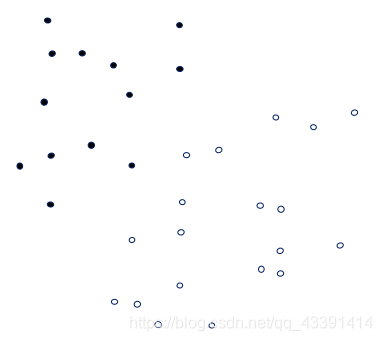
方案1（只看黑色分界线，红色不用管）

方案2（只看黑色分界线，红色不用管）

哪一个更好？
第二个好，将两类数据分得更开，而且：

建模

有了目标之后，我们要对上面那个更好的分界面进行数学描述：即希望拥有更大的间隔。间隔就是红色区域的宽度。
数学描述：
分界面的直线设为：

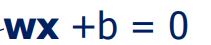
样本点x到该分界面的距离为（使用点到直线距离公式）：

该直线选得好不好？看间隔。

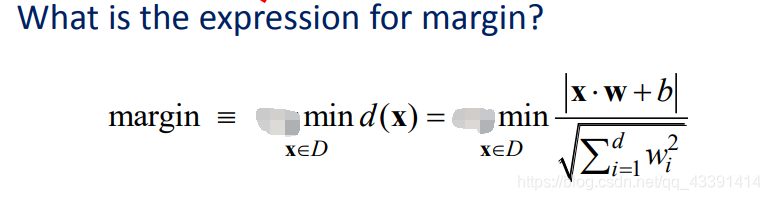
稍微解释一下，一般我们认为间隔是上面公式的两倍，即红色区域的宽度，但是我们的目标是间隔越大越好，其实也就是间隔的一半越大越好，所以我们没乘2也是可以的，不影响什么。

最后，算出了间隔之后，我们希望我们选的直线（由w,b决定）间隔是最大的。即：

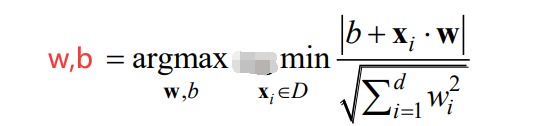
通俗的解释就是，我们先穷举一个w,b（定下一条直线），然后看下间隔，看大不大，不大就穷举下一个参数w,b，直到找到最大的那个间隔，此时返回对应的参数w,b。这样，就求解完成了。

远没有完成，我们忘记了约束。我们一心只管间隔最大，忘了去测试一下间隔最大对应的那个直线能否分对我们的样本。
为了便于数学处理，我们的所有点都预处理成$(x_i,y_i)$的格式，其中$y_i$是标签，我们预处理成$+1$或者$-1$。一个代表正类，一个代表负类。因此，直线可以分对样本也就是：

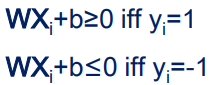
合起来就是：

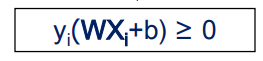
最终得到：

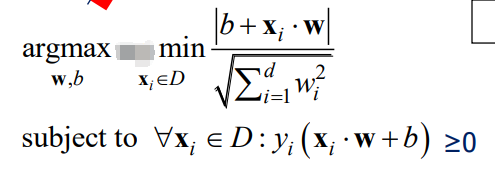
考虑将上述约束变成：

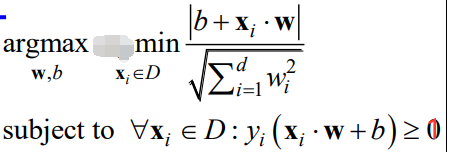
有人说，改成1，这怎么可以呢？答案是：可以的，而且在线性可分的情况下是等价的。
解释：我们先忽略掉上面两幅图的等于号，变成大于号，因为在完全线性可分的情况下，两类样本在直线的两侧，不会在直线上，所以不会为0，不取等号。
然后假设上上幅图选出来的最佳参数是w,b，且$y_i(w{x}_i+b)=m>0$，那么我们可以找一个比较大的正数k，令W=kw,B=kb,然后可以证明这个是上幅图的最优解。
证明很简单
第一，系数乘以一个倍数，内层公式的结果不受系数倍数影响，分子分母会约掉，所以原来是最大间隔，现在还是最大间隔。

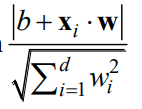
第二，由于我们乘了一个比较大的系数，从而有$y_i(W{x}_i+B)=km>1$，满足上幅图的第二个约束。
结论：上上幅图的约束转化为上幅图的约束后，分别求出来的最优直线关系密切，它们所对应的直线是同一条（考虑$x+2=0,2x+4=0$，间隔没有变大。但是乘了倍数的后者却可以使得

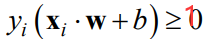
也即：

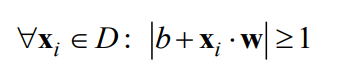
那么我们以后就只用第二个形式了。

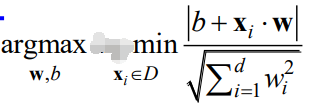
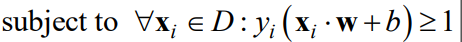
继续向前推导，我们有

现在精彩的时候到了，如果我们让$||w||$特别小，那么上面等式的右边就会特别大，从而任意的样本带入，左边都会特别大，在所有这么大的当中选一个最小的，也就是间隔，自然也会变得非常大。基于这个思想，我们又改了目标函数。

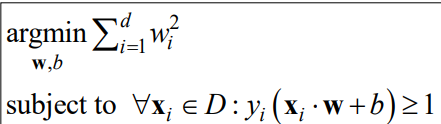
当然了，对于上面，还有一种几何解释，下面请看。

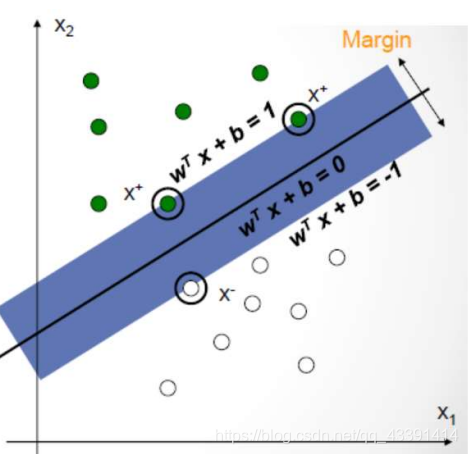
我们要选择满足约束的w,b。即如上图，要使得分对，且

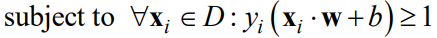
上图的那个直线分对了样本，但是能做到分对的有很多，哪个才是我们要的那个最大间隔，这才是我们的目标。我们发现，这两条线($w^{T}x+b=1,w^{T}x+b=-1$）之间的距离（使用两条平行线的距离公式）是：

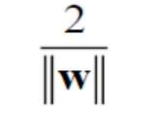
也就是说:这个是间隔，所以我们要最大化，但是发现不就是最小化下面这个吗：

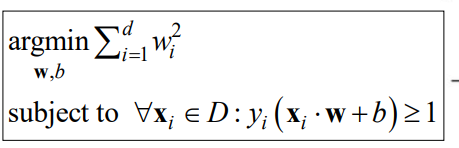
所以又回来了！
另外，借此处引入一个
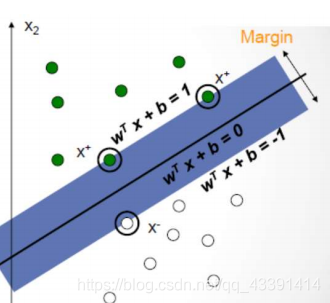
概念：支持向量(support vector)，它表示分界线两端的最前线。比如下面的画圆圈的3个点就是支持向量。
含义：你可以把其他数据点都去掉，然后就用这3个点进行SVM训练求解，你会发现分界线还是这一条，这也是名字由来：支持向量。把其中任何一个支持向量删除都可能会改变分界线。

求解

这能解吗？能，这是2次规划，留给数学就行了。为了科普，给出2次规划的形式。

小总结

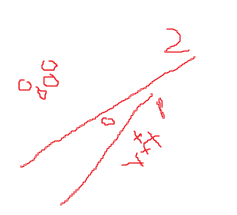
如果线性可分，上面就已经解决所有问题了。上面一般称作硬间隔支持向量机(hard-margin SVM)，即必须要求数据线性可分，但是对线性不可分则无能为力。而且对离群点非常敏感，因为可能会成为支持向量。比如下图，我们希望2是分界线，而不是1为分界线：

软间隔SVM

下图是一个线性不可分的样本点，使用硬间隔SVM来进行分类，将无能为力，没法得到解。

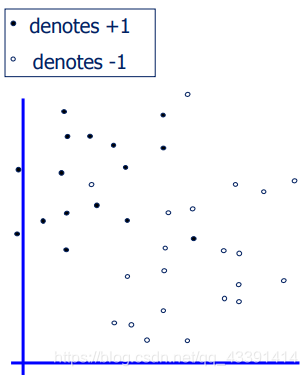
因此，我们稍微改动一下模型，我们现在给所有样本一些松弛，例如：

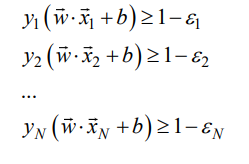
原来是要严格>=1，现在不要求，即对于那些异常点允许分错，允许其值小于0，这个点对应的$\epsilon$是一个大于1的正数。
但是，我们光这样是不够的，应该对所有的$\epsilon$进行适当地约束，否则我们取$\epsilon$为无穷大，那么下面的那些不等式都会成立，这样就没有优化的意义了。
我们在目标函数中希望$\epsilon$尽量小。即目标函数变为下面，并求最小。

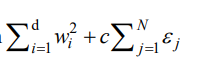
同时，我们要约束$\epsilon$大于等于0，因为没有分好的样本才应该进入第二项惩罚，分好了的样本应该是有>=1的，假设有一个分好的样本带入是100，那么模型会选择$\epsilon$为-99，从而损失函数瞬间小了很多，这会非常影响其他样本的分类，因为可能模型会损失其他样本分错来换取一个样本带入为1000，那么损失函数超小。
显然这不是我们想要的，所以要求$\epsilon$大于等于0，当等于0的时候，不就是我们以前的硬间隔吗？
我们发现：上面的$\epsilon$就是每个样本的损失，分对了的就为0。即下面这个图。

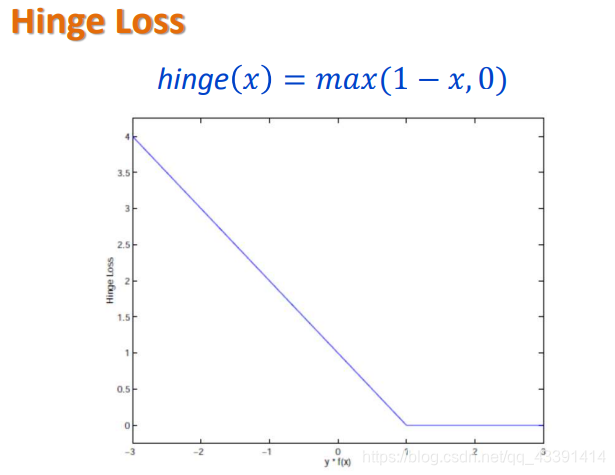
上面这个图表示一个样本带入之后，如果大于等于1，那么损失为0，否则分错的情况下，越分错损失越大。
一个补充：和0-1loss的联系和区别：

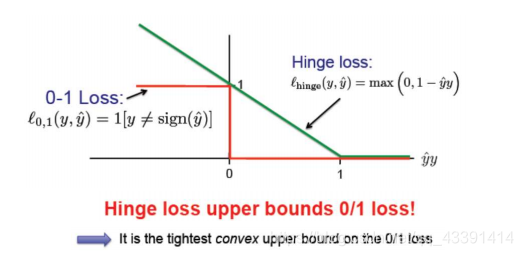
解释：0-1loss就是分对了就惩罚为0，分错了就一律为1，而hinge loss分得越错，惩罚越大。
那么回到求解问题，这个问题还是二次规划问题吗？
我们发现，我们多了N个变量$\epsilon$，但是没关系，我们把这也看作优化目标即可，发现目标还是二次的，不等式还是线性的（可以把$\epsilon$移到左边去，也当作一个优化的变量），那么就和平常的不等式没有什么两样了。