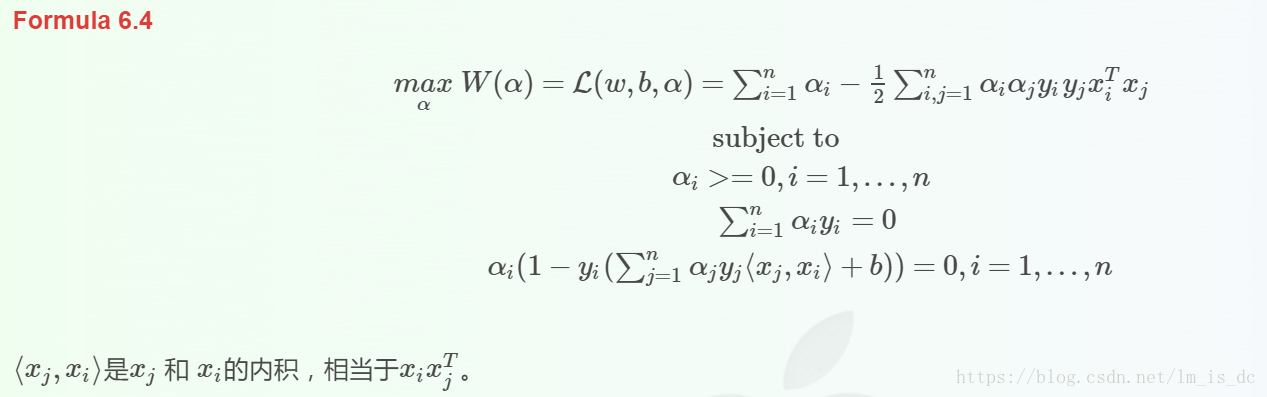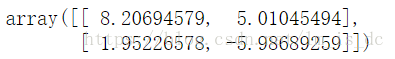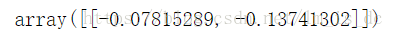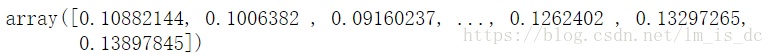机器学习之支持向量机SVM（Support Vector Machine）

支持向量机SVM（Support Vector Machine）

【关键词】支持向量，最大几何间隔，拉格朗日乘子法

一、支持向量机的原理

Support Vector Machine。支持向量机，其含义是通过支持向量运算的分类器。其中“机”的意思是机器，可以理解为分类器。
那么什么是支持向量呢？在求解的过程中，会发现只根据部分数据就可以确定分类器，这些数据称为支持向量。
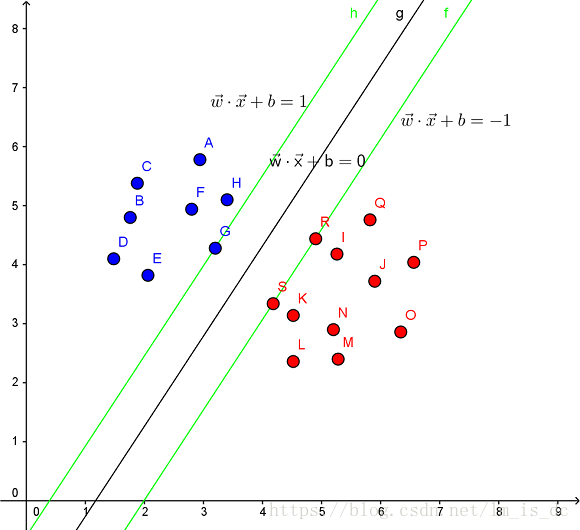
见下图，在一个二维环境中，其中点R，S，G点和其它靠近中间黑线的点可以看作为支持向量，它们可以决定分类器，也就是黑线的具体参数。

解决的问题：

• 线性分类

在训练数据中，每个数据都有n个的属性和一个二类类别标志，我们可以认为这些数据在一个n维空间里。我们的目标是找到一个n-1维的超平面（hyperplane），这个超平面可以将数据分成两部分，每部分数据都属于同一个类别。 其实这样的超平面有很多，我们要找到一个最佳的。因此，增加一个约束条件：这个超平面到每边最近数据点的距离是最大的。也称为最大间隔超平面（maximum-margin hyperplane）。这个分类器也称为最大间隔分类器（maximum-margin classifier）。 支持向量机是一个二类分类器。

• 非线性分类

SVM的一个优势是支持非线性分类。它结合使用拉格朗日乘子法和KKT条件，以及核函数可以产生非线性分类器。

SVM的目的是要找到一个线性分类的最佳超平面 f(x)=xw+b=0。求 w 和 b。

首先通过两个分类的最近点，找到f(x)的约束条件。

有了约束条件，就可以通过拉格朗日乘子法和KKT条件来求解，这时，问题变成了求拉格朗日乘子αi 和 b。

对于异常点的情况，加入松弛变量ξ来处理。

非线性分类的问题：映射到高维度、使用核函数。

线性分类及其约束条件

SVM的解决问题的思路是找到离超平面的最近点，通过其约束条件求出最优解。

最大几何间隔（geometrical margin）

求解问题w,b

我们使用拉格朗日乘子法(http://blog.csdn.net/on2way/article/details/47729419)
来求w和b，一个重要原因是使用拉格朗日乘子法后,还可以解决非线性划分问题。
拉格朗日乘子法可以解决下面这个问题：

消除w之后变为：

可见使用拉格朗日乘子法后，求w,b的问题变成了求拉格朗日乘子αi和b的问题。
到后面更有趣，变成了不求w了，因为αi可以直接使用到分类器中去，并且可以使用αi支持非线性的情况.

优势

SVM支持向量机，主要针对小样本数据、非线性及高维模式识别中表现出许多特有的优势，能解决神经网络不能解决的过学习问题，而且有很好的泛化能力。

函数：

SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0,
 shrinking=True, probability=False, tol=0.001, cache_size=200,
  class_weight=None, verbose=False, max_iter=-1,
   decision_function_shape=None, random_state=None)

参数的含义： 　

• C：float参数 默认值为1.0。错误项的惩罚系数。C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低，也就是对测试数据的分类准确率降低。相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。 　

• kernel: str参数 默认为‘rbf‘，算法中采用的核函数类型，可选参数有： 　　

  • linear：线性核函数 　　
  • poly：多项式核函数 　　
  • rbf：径像核函数/高斯核 　　
  • sigmod：sigmod核函数 　　
  • precomputed：核矩阵 　　
• degree :int型参数 (default=3)，这个参数只对多项式核函数（poly）有用，是指多项式核函数的阶数n，如果给的核函数参数是其他核函数，则会自动忽略该参数。 　　
• gamma：float参数，默认为auto核函数系数，只对’rbf’、 ‘poly’ 、 ‘sigmoid’有效。 如果gamma为auto，代表其值为样本特征数的倒数，即1/n_features。 　　
• coef0：float参数 默认为0.0 核函数中的独立项，只有对‘poly’和‘sigmod’核函数有用，是指其中的参数c 　　
• probability：bool参数 默认为False 是否启用概率估计。 这必须在调用fit()之前启用，并且会fit()方法速度变慢。 　　
• shrinking：bool参数 默认为True 是否采用启发式收缩方式。 　　
• tol: float参数 默认为1e^-3 svm停止训练的误差精度。 　　
• cache_size：float参数 默认为200 指定训练所需要的内存，以MB为单位，默认为200MB。 　
• class_weight：字典类型或者‘balance’字符串。默认为None 给每个类别分别设置不同的惩罚参数C，则该类别的惩罚系数为class_weight[i]*C，如果没有给，则会给所有类别都给C=1，即前面参数指出的参数C。 如果给定参数‘balance’，则使用y的值自动调整与输入数据中的类频率成反比的权重。 　　
• verbose ：bool参数 默认为False 是否启用详细输出。 此设置利用libsvm中的每个进程运行时设置，如果启用，可能无法在多线程上下文中正常工作。一般情况都设为False，不用管它。 　　
• max_iter ：int参数 默认为-1 最大迭代次数，如果为-1，表示不限制 　　
• random_state：int型参数 默认为None 伪随机数发生器的种子,在混洗数据时用于概率估计。

二、实战

1、分类

导包sklearn.svm

#导入支持向量机算法包，使用分类模型
from sklearn.svm import SVC
#导入生成聚类测试数据包
from sklearn.datasets import make_blobs
import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

获取数据

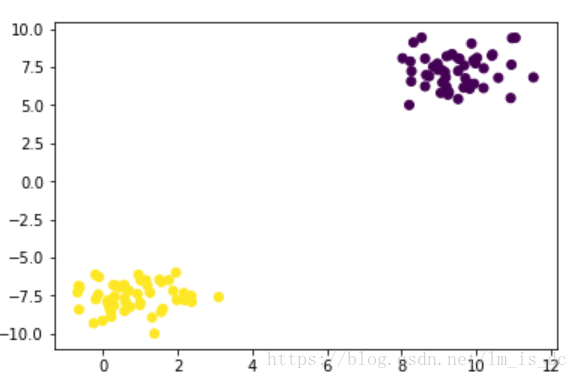
#生成两个聚类数据集
X,y = make_blobs(centers=2)
plt.scatter(X[:,0],X[:,1],c=y)

训练模型

#SVC算法使用线性内核函数
svc = SVC(kernel='linear')
#训练模型
svc.fit(X,y)
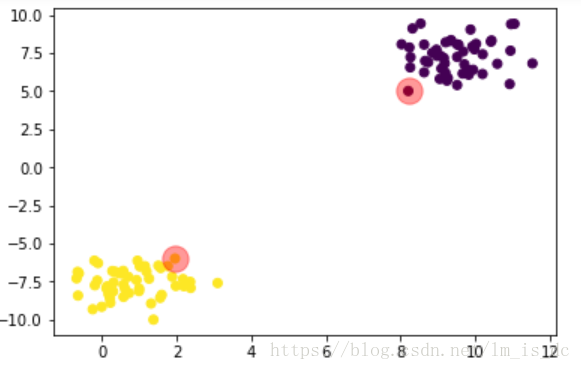
#查看各类所有的支持向量
support_vectors = svc.support_vectors_
support_vectors

数组的元素是两个坐标点。

plt.scatter(X[:,0],X[:,1],c=y)
#画出支持向量所在位置
plt.scatter(support_vectors[:,0],support_vectors[:,1],
            s=300,  #半径为300
            alpha=0.4,  #透明度为0.4
            color='r'  #红色
           )

获取斜率和截距

# 提取系数获取斜率
w_ = svc.coef_
w_

#获取截距
b_ = svc.intercept_
b_

#求出中线的斜率和截距
#三维立体空间的一条线
# f(x,y) = w_[0,0]*x w_[0,1]*y + b_
# 0 = w_[0,0]*x + w_[0,1]*y + b_
# y = -w_[0,0]/w_[0,1] * x -b_/w_[0,1]
w = -w_[0,0]/w_[0,1]
b =  -b_/w_[0,1]

#求出上边界和下边界截距
# y = w*x +b
b_up = support_vectors[0][1] -w*support_vectors[0][0]
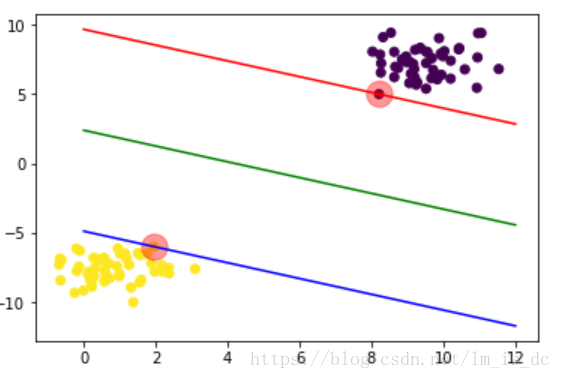
b_down = support_vectors[1][1] -w*support_vectors[1][0]

绘图

plt.scatter(X[:,0],X[:,1],c=y)
#画出支持向量所在位置
plt.scatter(support_vectors[:,0],support_vectors[:,1],
            s=300,  #半径为300
            alpha=0.4,  #透明度为0.4
            color='r'  #红色
           )
#画出回归线
x1 = np.linspace(0,12,100)
y1 = w*x1 + b
plt.plot(x1,y1,color='green')
plt.plot(x1,w*x1 + b_up,color='red')
plt.plot(x1,w*x1 + b_down,color='blue')

2、SVM分离坐标点

导包

#导入支持向量机算法包，使用分类模型
from sklearn.svm import SVC
#导入生成聚类测试数据包
from sklearn.datasets import make_blobs
import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

获取数据

#随机生成300个点
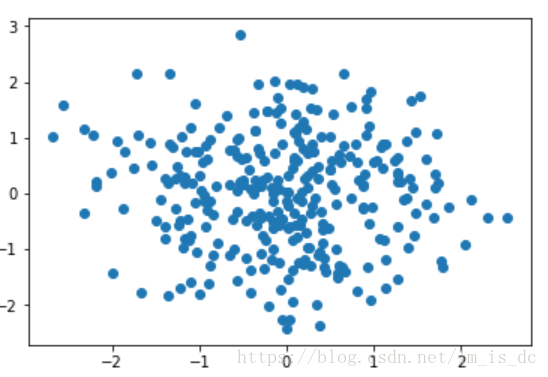
X = np.random.randn(300,2)
plt.scatter(X[:,0],X[:,1])

把坐标点分类

#第1、3象限分为一类，特点：(x,y)要么都为正，要么都为负
#第2、4象限分为一类，特点：(x,y)有正有负
#所以可以使用异或把坐标点分类
#异或操作(X[:,0],X[:,1])
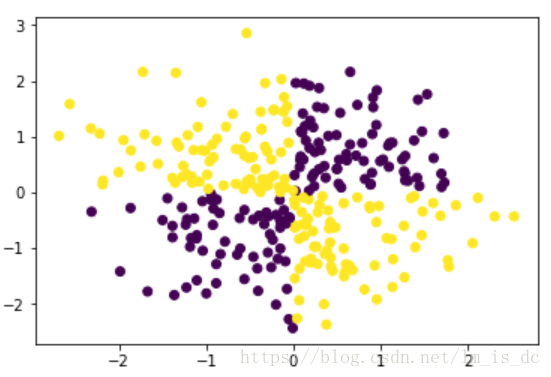
y = np.logical_xor(X[:,0] > 0, X[:,1] > 0)
plt.scatter(X[:,0],X[:,1],c = y)

训练模型

svc = SVC(kernel='rbf')
svc.fit(X,y)

选取坐标系中的一些点作为测试点

a = np.linspace(-3,3,100)

b = np.linspace(-3,3,100)
#把a和b进行网格交叉
A,B = np.meshgrid(a,b)
#把A,B进行列与列合并，形成坐标点
X_test = np.concatenate([A.reshape(-1,1),
                        B.reshape(-1,1)],
                        axis = 1)
plt.scatter(X_test[:,0],X_test[:,1])

绘制测试点到分离超平面的距离

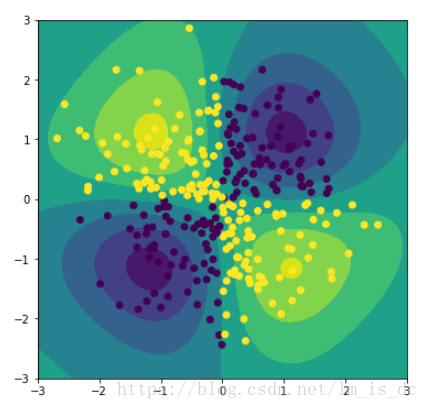
#计算样本点到分割超平面的函数距离
d_ = svc.decision_function(X_test)
d_

把二维的点投射到三维空间中，在两类点中有一个超平面，其中一类的的点在超平面的上面，另一类的点在超平面的下面。

绘制等高线图

plt.figure(figsize=(6,6))
#绘制等高面
plt.contourf(A,B,d_.reshape(100,100))

plt.scatter(X[:,0],X[:,1],c = y)

# 绘制等高线
plt.contour(A,B,d_.reshape(100,100))

3、使用多种核函数对iris数据集进行分类

导包

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt

import sklearn.datasets as datasets

%matplotlib inline

获取数据

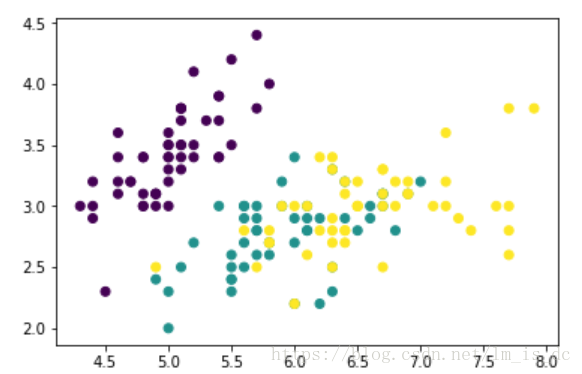
iris = datasets.load_iris()
#提取数据只提取两个特征，方便画图
X = iris.data[:,:2]
y = iris.target
plt.scatter(X[:,0],X[:,1],c = y)

训练模型

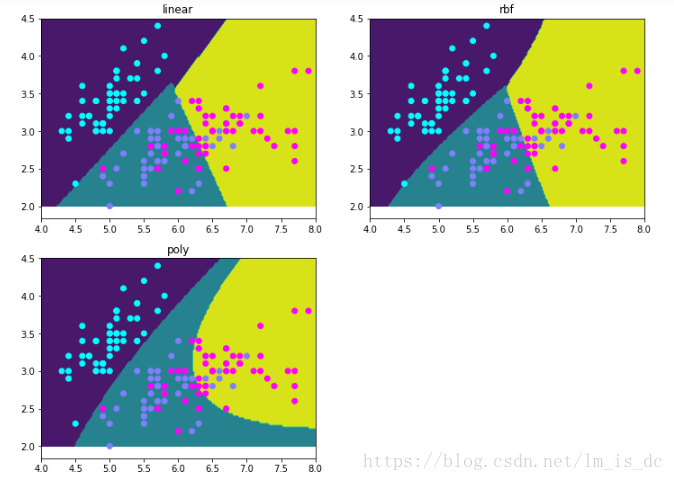
estimators = {'linear':SVC(kernel = 'linear'),
             'rbf':SVC(),
             'poly':SVC(kernel = 'poly')
            }
for key,estimator in estimators.items():
    estimator.fit(X,y)

获取测试点

x1 = np.linspace(4,8,200)
y1 = np.linspace(2,4.5,100)

X1,Y1 = np.meshgrid(x1,y1)
#合并X1,Y1成为坐标点
X_test = np.c_[X1.ravel(),Y1.ravel()]

预测

result_ = {}
for key,estimator in estimators.items():
    y_ = estimator.predict(X_test)

    result_[key] = y_

绘图

plt.figure(figsize=(12,9))
for i ,key in enumerate(result_):

    axes = plt.subplot(2,2,i+1)

    axes.contourf(X1,Y1,result_[key].reshape(100,200))
    axes.scatter(X[:,0],X[:,1],c = y,cmap = 'cool')
    axes.set_title(key)

4、使用SVM多种核函数进行回归

导包

#SVR为支持向量机回归算法包
from sklearn.svm import SVR
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

获取数据

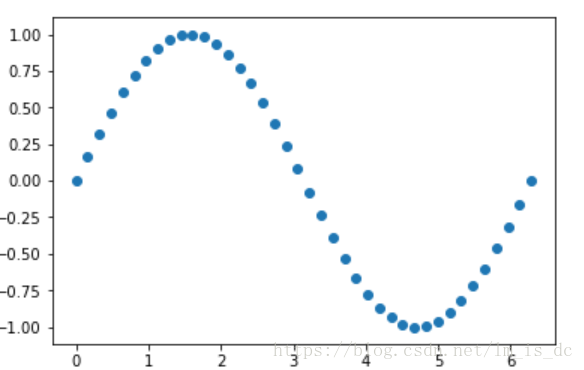
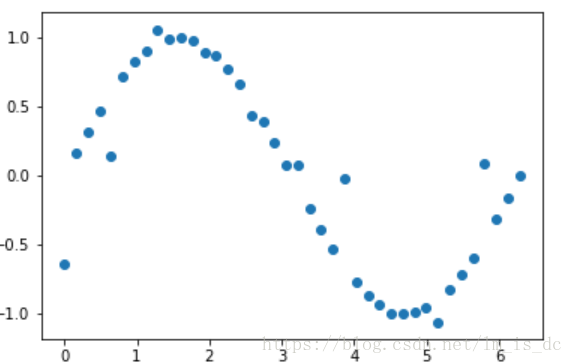
X = np.linspace(0,2*np.pi,40).reshape(-1,1)
y = np.sin(X)
plt.scatter(X,y)

#数据加噪
y[::4] += np.random.randn(10,1)*0.3
plt.scatter(X,y)

训练模型

#创建三个模型，分别使用不同的内核函数
models = {'linear':SVR(kernel='linear'),
         'rbf':SVR(), #kernel='rbf' 默认值
          'poly':SVR(kernel='poly')
         }
#测试数据
X_test = np.linspace(0,2*np.pi,150).reshape(-1,1)
result_ = {}
#训练模型并预测数据
for key,model in models.items():
    model.fit(X,y)
    y_ = model.predict(X_test)
    result_[key] = y_

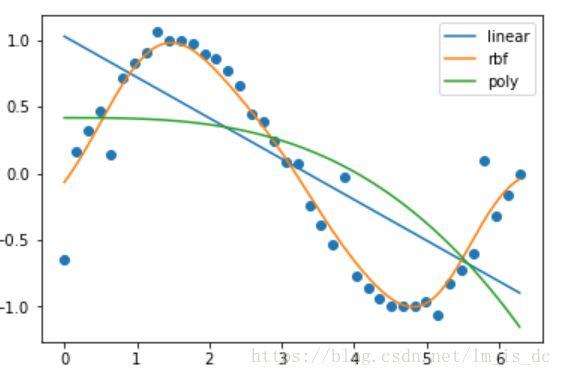
绘图

plt.scatter(X,y)
for key,y_ in result_.items():
    #显示图例
    plt.plot(X_test,y_,label=key)
    plt.legend()

可以看出在这个例子中，基于半径(rbf)的SVR模型预测结果更准确。