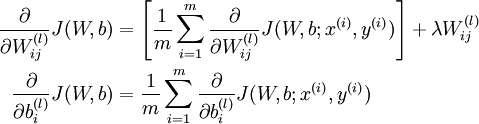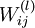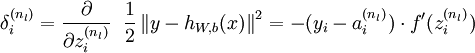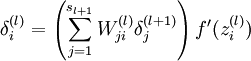反向传播算法的理解

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/hzhj2007/article/details/79927106

    BP(Backpropagation Algorithm，反向传播算法)在神经网络学习中有着无可替代的作用，关于其优化方法可阅读该文章《一文看懂各种神经网络优化算法：从梯度下降到Adam方法》。本文仅立足于反向传播的实现过程。文中如有理解偏差，请各位指正。

    就反向传播的字面理解是将数据从后(输出)向前(输入)传递，数据的具体形式是代价函数对其超参数(权重(W)和偏置(b))的偏导数，反向传播的目的是使代价函数达到最小。所以该算法的根本是代价函数对权重和偏置的偏导数的计算方法。所以“反向传导算法”的翻译还是很贴切的。

    首先，看下常见代价函数的形式，公式来自这里。

                                              （二次代价函数）

                       （交叉熵代价函数）

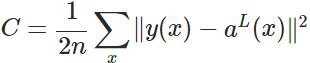
    式子中，n表示样本数目，C为批样本的代价函数，y(x)表示真实样本的输入x和输出y(x)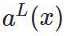，表示网络输出层（即第L层)对输入x的输出值(网络的激活值)。所以反向传播算法需要根据具体的代价函数的形式进行计算。

    二次代价函数的实际使用中，为减小权重的幅度，防止过度拟合，加入了权重衰减项，变换后的公式如下(后文中的公式均来之这里)。

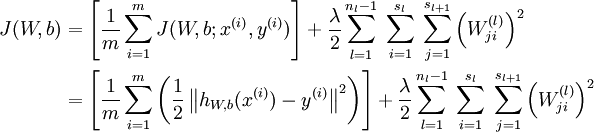
    此时其偏导数的形式为：

    第一行比第二行多出一项，是因为权重衰减项作用于W而不是b

    其次，复述下反向传播算法的思路。

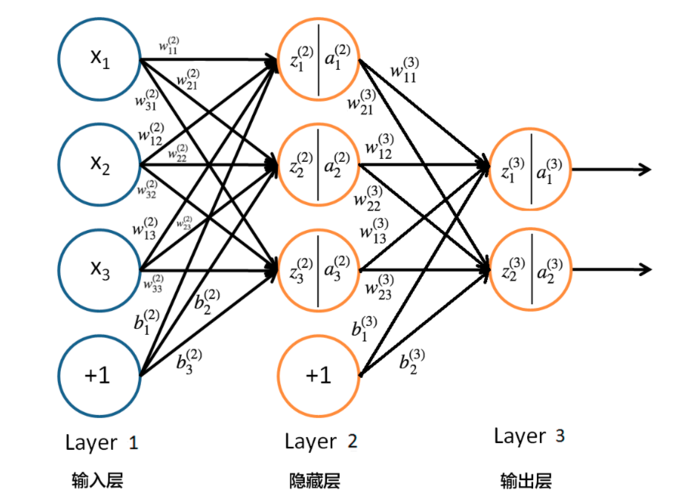
    为方便后文公式中符号的理解，可根据下图进行对比，图片来自这里。

    其中，z和a分别表示神经元的输入和输出(激活函数作用于输入后的结果)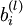，表示第l层的权重和偏置，i表示第l层的神经元序号，j表示第l-1层神经元的id。

    接着，着重理解偏导的计算过程。公式中由于涉及到后一层的加权值(即z值)和多层间的数值使得计算显得有点复杂。

    对输出层神经元而言，代价函数相对于该层输入的梯度计算公式如下。

        

    其计算过程如下。

    对隐层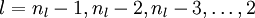来说，第l层的第i个节点输入的梯度计算公式如下。

    其计算过程如下。

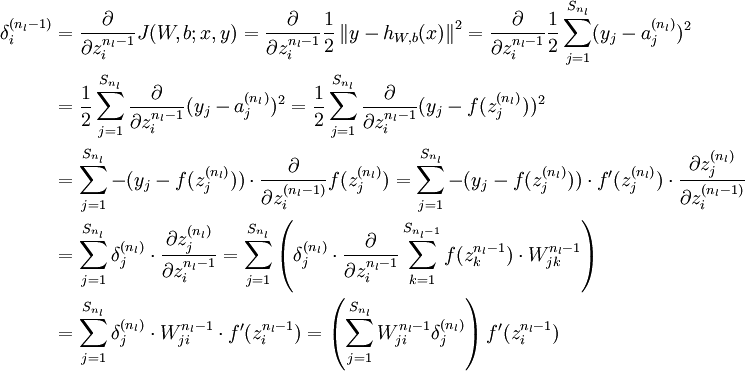
    其计算过程也可根据链式法则递归求解，即代价函数对第l层输入的梯度等于{(代价函数对第l+1层输入的梯度)*(第l+1层的输入相对于第l层输入的梯度)}，由于第l+1层有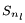个节点，故需要将每个节点计算的梯度值相加获得代价函数相对于第l层第i个节点输入的梯度值。

    得到神经元输入的梯度后，利用输入与权重和偏置的关系，可获得如下公式，即为最终需要计算的梯度。

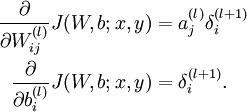
    最后，权重和偏置的更新公式如下，其中a为学习率。

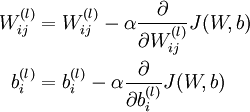
参考文献：

1. http://deeplearning.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95
   
2. http://www.cnblogs.com/zhonghuasong/p/7079443.html
   
3. https://zhuanlan.zhihu.com/p/27449596
   
4. https://www.jianshu.com/p/679e390f24bb