算法分析——排序算法（归并排序）复杂度分析（主定理法）

前两篇文章中分别是要用递归树、代换法对归并排序的时间复杂度进行了简单的分析和证明，经过两次分析后，我们发现递归树法的特点是：可以很直观的反映出整个归并排序算法的各个过程，但因为要画出递归树所以比较麻烦，所以递归树算法更适合新手，因为它可以让分析者更直观、简易的理解递归式算法的各个过程并对各个过程的分析、合并，但因为需要要画递归树，所以比较复杂。代换法也仅适合在已经大致猜测出算法的复杂度的时候，对猜测解进行证明。那有没有一种分析方法即可以在没有事先明确算法复杂度的大致解，又可以让分析者在较短的时间算出算法的复杂度？

数学定义

今天这篇文章讲述的主定理法就可以通过套用公式简单、快速算出递归式算法的复杂度。下面我们首先描述下主定理法的数学定义：

递归式 $T(n) = aT(\frac{n}{b}) + f(n)$ ，函数 $T(n)$ 需要满足设 $a\geq 1，b> 1$ ， $b > 1$ ， $f(n)$ 为正函数， $\frac{n}{b}$ 可能是 $\frac{n}{b}$ 或 $\left \lfloor \frac{n}{b} \right \rfloor$ 或 $\left \lceil \frac{n}{b} \right \rceil$ 递归式函数 $T(n)$ 可能的渐进界有以下三种可能：

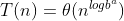
1.若存在某常数 $\varepsilon > 0$ ，都有 $f(n) = O(n^{({log_{b}}a)-\varepsilon })$ ，则 $T(n) = \theta (n^{^{{log{b}}^{a}}})$

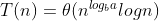
2.若 $f(n) = \theta (n^{{log_{b}}^{a}})$ ,则 $T(n) = \theta (n^{{log_{b}}{a}}logn)$

3.若存在某常数 $\epsilon > 0$ ，有 $f(n)=Ω(n^{{log_{b}}^{a}+\varepsilon })$ $f(n) = \Omega (n^{({log_{b}}{a})+\varepsilon })$ ，且存在某常数 $c< 1$ 与所有足够大的n，有 $af(\frac{n}{b}) \leq cf(n)$ ，则 $T(n) = \Theta (f(n))$

了解了主定理的数学定义之后，我们只需要将归并排序的递归式代入到主定理的数学公式中，即可在很短的时间内获得归并排序的时间复杂度，下面就会给出证明过程。

归并排序时间复杂度求解

对于归并排序的时间复杂度函数 $T(n) = 2T(\frac{n}{2}) + O(n)$ ，可知 $a=2,b=2,f(n) = O(n)$ ，所以符合第二种情况，由此可得 $T(n) = \Theta (nlogn)$ 。

看到这里，大家是不是觉得主定理法在解归并排序或者说在解递归算法的复杂度函数式时，特别的方便和快捷。但现在应该还会有很多人在疑惑主定理这么好用，但这个公式是怎么的来的？在任何情况下的递归式都可以使用吗？怎么证明这个公式是正确的？

主定理公式证明

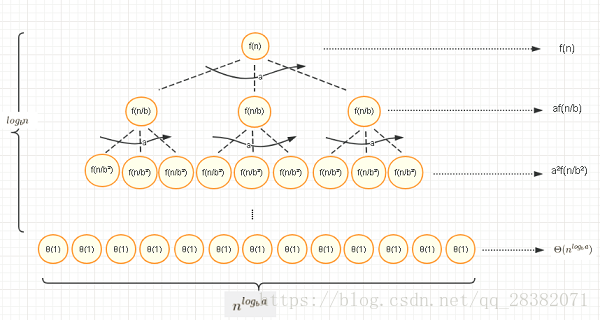
由上述的数学定义中可知，b在取值时可分为三种情况，即第一种n可被b整除时取 $\frac{n}{b}$ ，第二种n不可被b整除时取 $\left \lfloor \frac{n}{b} \right \rfloor$ ，第三种n不可被b整除时取 $\left \lceil \frac{n}{b} \right \rceil$ 。这里首先使用n可被b整除的情况进行证明。在进行公式证明之前，这里做个简单而且更直观的图形化解读，这样可以让一些基础比较差的同学更好的理解主定理的数学定义。

由下图我们可以得知，递归树的根节点为 $f(n)$ ，随后每往下一层都会分裂为a个问题规模为 $f(\frac{n}{b})$ 的子节点，分裂 ${log_{b}}{a}$ 次后分裂结束，此时分裂出 $n^{{log_{b}}{a}}$ 叶子节点，叶子节点的问题规模为 $\Theta (1)$ 。由递归树可得

$T(n) = \sum_{j=0}^{({log_{b}}{n})-1}a^{j}f(\frac{n}{b^{j}}) + \Theta (n^{{log_{b}}{a}})$

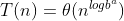
证明1.若存在某常数 $\varepsilon > 0$ ，都有 $f(n) = O(n^{({log_{b}}a)-\varepsilon })$ ，则 $T(n) = \theta (n^{^{{log{b}}^{a}}})$

$f(\frac{n}{b^{j}}) = O((\frac{n}{b^{j}})^{({log_{b}}{a})-\varepsilon}) = c(\frac{n}{b^{j}})^{({log_{b}}{a})-\varepsilon}$

$T(n) = \sum_{j=0}^{({log_{b}}{n})-1}a^{j}f(\frac{n}{b^{j}}) + \Theta (n^{{log_{b}}{a}}) \leq \sum_{j=0}^{({log_{b}}{n})-1}c.a^{j} (\frac{n}{b^{j}})^{({log_{b}}{a})-\varepsilon} + \Theta (n^{{log_{b}}{a}})$

$T(n) = cn^{({log_{b}}{a}) - \varepsilon } \sum_{j=0}^{({log_{b}}{n})-1}\frac{a^{j}}{(b^{({log_{b}}{a})-\varepsilon })^{j}}+ \Theta (n^{{log_{b}}{a}})$

$T(n) =cn^{({log_{b}}{a}) - \varepsilon } \sum_{j=0}^{({log_{b}}{n})-1}\frac{a^{j}}{(\frac{a}{b^{\varepsilon }})^{j}} + \Theta (n^{{log_{b}}{a}})$

$T(n)= cn^{({log_{b}}{a}) - \varepsilon } \sum_{j=0}^{({log_{b}}{n})-1}(b^{\varepsilon })^{j} + \Theta (n^{{log_{b}}{a}})$

这时可以看出 $\sum_{j=0}^{({log_{b}}{n})-1}(b^{\varepsilon })^{j}$ 其实是个等比序列，等比序列求和公式 $S(n) = a1.\frac{1-q^{n}}{1-q}$ ， $a1$ 为序列首项,q为公比，所以可得

   $T(n)= cn^{({log_{b}}{a}) - \varepsilon }.\frac{1-(b^{\varepsilon })^{{log_{b}}{n}}}{1-b^{\varepsilon }} + \Theta (n^{{log_{b}}{a}})$

   $T(n) = cn^{({log_{b}}{a}) - \varepsilon }.\frac{1-n^{\varepsilon }}{1-b^{\varepsilon }}+ \Theta (n^{{log_{b}}{a}}) = cn^{({log_{b}}{a}) - \varepsilon }\frac{n^{\varepsilon }-1}{b^{\varepsilon }-1}+ c1. n^{{log_{b}}{a}}$

   $T(n) =\frac{1}{b^{\varepsilon }-1}(cn^{({log_{b}}{a})-\varepsilon }n^{\varepsilon }-cn^{({log_{b}}{a})-\varepsilon })+ c1. n^{{log_{b}}{a}}$

   $T(n) = \frac{1}{b^{\varepsilon }-1}(cn^{{log_{b}}{a}}-cn^{({log_{b}}{a})-\varepsilon }) + c1. n^{{log_{b}}{a}}$

因为 $\varepsilon > 0$ ，所以 $T(n)$ 的最高阶则为 $n^{{log_{b}}{a}}$ ，所以 $T(n) = \theta (n^{^{{log{b}}^{a}}})$ 。情况1证毕。

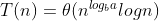
证明2.若 $f(n) = \theta (n^{{log_{b}}^{a}})$ ,则 $T(n) = \theta (n^{{log_{b}}{a}}logn)$

   $f(\frac{n}{b^{j}}) = \Theta ((\frac{n}{b^{j}})^{{log_{b}}{a}})$

$T(n) = \sum_{j=0}^{({log_{b}}{n})-1}a^{j}f(\frac{n}{b^{j}}) + \Theta (n^{{log_{b}}{a}})$

   $T(n) = \Theta( \sum_{j=0}^{({log_{b}}{n})-1}a^{j}((\frac{n}{b^{j}})^{{log_{b}}{a}})) + \Theta (n^{{log_{b}}{a}})$

   $T(n) = \Theta( n^{{log_{b}}{a}}\sum_{j=0}^{({log_{b}}{n})-1}\frac{a^{j}}{a^{j}}) + \Theta (n^{{log_{b}}{a}})$

根据公式可得 $T(n) = \Theta ({n^{{log_{b}}{a}}log_{b}}{n})$ ，再根据对数函数的换地公式最后可得 $T(n) = \Theta ({n^{{log_{b}}{a}}log_}{n})$ 。情况2证毕。

证明3.若存在某常数 $\epsilon > 0$ ，有 $f(n) = \Omega (n^{({log_{b}}{a})+\varepsilon })$ ，且存在某常数 $c< 1$ 与所有足够大的n，有 $af(\frac{n}{b}) \leq cf(n)$ ，则 $T(n) = \Theta (f(n))$

$T(n) = \sum_{j=0}^{({log_{b}}{n})-1}a^{j}f(\frac{n}{b^{j}}) + \Theta (n^{{log_{b}}{a}})$

$\because af(\frac{n}{b}) \leq cf(n)$

   $\therefore a^{j}f(\frac{n}{b^{j}}) \leq c^{j}f(n)$ ①

$T(n) \leq \sum_{j=0}^{({log_{b}}{n})-1}c^{j}f(n) + \Theta (n^{{log_{b}}{a}}) = f(n)\sum_{j=0}^{({log_{b}}{n})-1}c^{j} + \Theta (n^{{log_{b}}{a}})$

   $T(n) \leq f(n) \sum_{j=0}^{\propto }c^{j} + \Theta (n^{{log_{b}}{a}})$

   $\because c<1 \therefore T(n) \leq \frac{1}{1-c}f(n) + \Theta (n^{{log_{b}}{a}})$

   $\because f(n) = \Omega (n^{({log_{b}}{a})+\varepsilon })$ 所以 $f(n)$ 的最高阶大于 $\Theta (n^{{log_{b}}{a}})$ 的最高阶

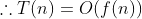
$\therefore T(n) = O(f(n))$

$T(n) = \sum_{j=0}^{({log_{b}}{n})-1}a^{j}f(\frac{n}{b^{j}}) + \Theta (n^{{log_{b}}{a}})$

$T(n) = f(n) + af(\frac{n}{b}) + ...+ a^{{log_{b}}{a}}f(\frac{n}{b^{{log_{b}}{a}}}) + \Theta (n^{{log_{b}}{a}})$

$T(n) = \Omega (f(n))+ \Theta (n^{{log_{b}}{a}})= \Omega (f(n))$

由 $T(n) = O(f(n))$ 和 $T(n) = \Omega (f(n))$   可得 $T(n) =\Theta (f(n))$ 。情况3证毕。

至此，在n可以被b整除的情况已经证明完毕，因为篇幅问题，这里不在对n不可以被b整除的另外两种情况证明，有兴趣的同学可以网上搜索一下，资料很多。经过了详细的数学公式证明后，相信很多人已经了解了主定理的证明。但此时应该还有很多人疑惑，为什么主定理分为了三种情况，这三种情况又是依据什么进行划分的？数学基础比较好的同学现在应该已经理解，这里将做一个简单的文字阐述，以便数学基础较差的同学理解。

由上图的递归树可得知，整个递归树的复杂度是由递归树中各层节点的加和所得。而每层节点的复杂度也是呈数学级数改变。而主定理的三种情况就是根据每层节点复杂度递增或递减时的数学级数的不同所制定。

第一种情况：节点的复杂度随着递归树的深度越深而呈几何级数（甚至更高）单调递增，所以在递归树的叶子节点的复杂度的阶数是最高的，也就是说递归式的复杂度由叶子节点复杂度的阶数所决定，所以 $T(n) = \theta (n^{^{{log{b}}^{a}}})$ 。

第三种情况：节点的复杂度随着递归树的深度越深而呈几何级数（甚至更高）单调递减，所以在递归树的根节点的复杂度的阶数是最高的，也就是说递归式的复杂度由叶子节点复杂度的阶数所决定，所以 $T(n) = \Theta (f(n))$ 。

第二种情况：节点的复杂度随着递归树的深度越深而呈较小级数（甚至不变）单调递减或递减，所以在递归树的各个节点的复杂度的阶数相似，也就是说递归式的复杂度由所有子节点复杂度的阶数所决定，而由于每层节点的复杂度变动较小（甚至不变），所以在渐进角度看，可以认为每层所有节点的复杂度之和大致相同为 $\theta (n^{^{{log{b}}^{a}}})$ ，所以 $T(n) = \theta (n^{{log_{b}}{a}}logn)$ 。

注释①：得到该公式的过程，此处不在详述，大致意思为递归树中每往下一层，子节点的复杂度便会降低父节点的复杂度的c倍（ $c< 0$ ），此处可以也写为 $a^{j}f(\frac{n}{b^{j}}) \leq cf(n)$ ，不过这样的写法并不是渐进紧确的。

算法分析——排序算法（归并排序）复杂度分析（主定理法）

数学定义

归并排序时间复杂度求解

主定理公式证明

猜你喜欢