前面对算法分析的一些常用的 渐进符号 做了简单的描述,这里将使用归并排序算法做为一个实战演练。
这里首先假设读者对归并排序已经有了简单的了解(如果不了解的同学可以自行百度下归并排序的原理)。了解此算法的同学应都知道,归并排序的主要思想是 分而治之(简称分治)。分治算法的基本模式也基本上分为以下三大步骤:
1.问题分解成若干子问题,使子问题的解决起来足够简单,甚至达到常量级别θ(1)
2.子问题解决
3.合并
在算法分析中也将会根据这三大步骤进行复杂度的分析和合并。下面将给出伪代码,并针对伪代码进行复杂度分析。
伪代码
// Merge Sort Code
MergeSort(A,start,end){
if(start < end)
then mid <- floor[(start-end)/2]
MergeSort(A,start,mid);
MergeSort(A,mid,end);
Merge(A,start,mid,end);
}
// Merge Code
Merge(A,start,mid,end){
// 创建左数组
left <- mid - start + 1;
create arrays L[1...left];
for i <- 1 to left
L[i] = A[start + i -1];
// 创建右数组
right = end - mid;
create arrays R[1...right ];
for j <- 1 to right
R[j] = A[mid + j];
// 合并
i <- 1;
j <- 1;
for k <- start to end
do if L[i] <= R[j]
then A[k] = L[i];
i++;
if i > left
then TailInsert(A,start + k,R,j) break;
else A[k] = R[j];
j++;
if j > right
then TailInsert(A,start + k,L,i) break;
}
// 直接将B中的起始位置为q至结尾的元素插入到A数组的p起始位置
TailInsert(A,p,B,q){
k <- 0;
for i <- q to length(B)
A[p + k] = B[i];
k++;
}空间复杂度
由伪代码可以看出,归并排序实现的主要实现的原理是由上至下递归的二分原数组,并由下至上递归的合并二分后的子数组,由于每次数组的分裂都需要建立两个新的数组,所以其实归并排序的空间复杂度是较高的,可达到O(n)。可能有些小伙伴会在空间复杂度到底是O(n)还是O(nlogn)之间存在疑惑,因为由伪代码可以得出归并算法的整个过程会复制log(n)个大小为n的数组,那为什么空间复杂度不是O(nlog(n))呢?①
时间复杂度
通过伪代码可以看出,归并排序通过分治和递归对数组A进行不断的问题分解和合并,而针对递归式的算法分析, 算法导论中讲述了多种方法,例如代换法、递归树法、主方法。下面将使用多种方式对归并排序进行复杂度的增长量级进行分析。
由于代换法需要事先估测一个大致的值,然后才能做进一步的代换验证,而递归树法是比较适合预测一个估值,所以我们首先将使用递归树法进行时间复杂度的分析。

递归树法分析
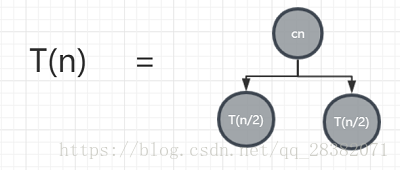
假设输入规模n时,归并算法的时间复杂度为T(n),由伪代码可知归并算法中分为两步:子数组排序、子数组合并,由此可得T(n)= 2T(n/2 )+ cn , c为大于0的一个常数。如果将该公式用树形结构来表示的话,则如下所示:
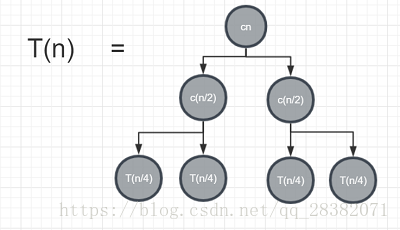
因为T(n)= 2T(n/2 )+ cn,可得T(n/2)= 2T(n/4)+ c(n/2),所以T(n)则可以推出下图:
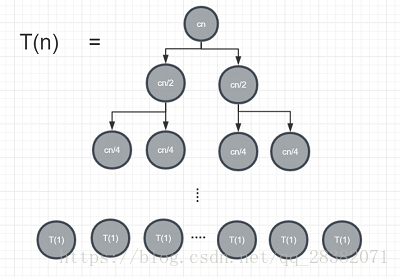
依次递推可以得到一个深度为,叶子节点个数为n,值为T(1)的树形图。如下图所示:
此时将树形图中所有的节点进行加和即可得到归并排序的时间复杂度 ②
标注①
1.程序的执行是在线程栈中,一次方法的调用和返回代表着一个栈帧的入栈和出栈,栈帧出栈后,该栈帧中的临时变量所占用的空间都会得到释放
2.copy数组的操作都是在merge方法中执行,而merge方法的执行是在MergeSort的尾部,再加上程序执行的顺序性和递归的特点,也就是说整个算法所在的线程栈中只会存在一个merge方法,而merge方法从下往上依次归并的时候,merge方法所需要的空间分别为2,4,8......n,直到return到第一层MergeSort方法时,merge方法所需要的空间才会达到最高n,由于递归从底层依次返回到上一层时,底层栈帧所占用的空间就会得到释放,所以归并算法的空间复杂度在递归返回到首层栈帧时最大,为O(n)。
标注②