高三数学学习的第一课----不等式的解法
1.一元二次不等式
1.1 数字系数的一元二次不等式,如\(x^2<3\),\(x^2+2x<0\),\(x^2-3x+2<0\)
1.2 字母系数的一元二次不等式,如\(x^2-(a+a^2)x+a^3<0.(a\neq0)\)
1.3 能转化为一元二次不等式,如\((x^2-3x+2)\cdot(x+1)<0,2^{x^2-x}<4\),
如果能理解不等式中的\(x\)的内涵,\(x\Rightarrow 代数式\),则可以解决诸如这样的不等式,\((2^x)^2-3\cdot 2^x+2<0\),或者\((log_2^{\;\; x})^2-3\cdot log_2^{\;\;x}+2<0\)
2.高次不等式
2.1 高次不等式,如\((3x^2-2x+1)\cdot(x^2-1)<0\)
2.2 分式不等式,如\(\cfrac{2x^2-3x+1}{x-2}>0\);\(\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)
3.绝对值不等式
3.1 基本类型,如 \(|x-1|<0 ,2<|x+3|<3\)
3.2 带有两个绝对值符号的不等式,如\(|x+1|+|x-2|<3\)
3.3 带有两个绝对值符号的不等式的求解,如\(|x-2|\ge |2x+1|\)
3.4 带有两个绝对值符号的不等式的转化,如\(|x-2|\ge |y-4|(x\in [1,2])\)
3.5 带有双层绝对值符号的不等式的转化,如\(|2|x|-1|\leq 1\)
4.对数不等式
- \(log_2^{\,\,x}<1\),\(log_2^{\,\,(x-2)}<log_2^{(2x+1)}\), \(log_2^{\,\,(x+1)}<2.5\)
5.指数不等式
- \(2^x>3\),\(3^{x^2+3x-1}<(\cfrac{1}{3})^{2x-1}\),\(e^x>2\)
- \(81\times3^{2x}\ge (\cfrac{1}{9})^{x+2}\)
- \(2^{2x+2}+3\times2^x-1\ge 0\)
6.三角不等式
\(2sinx>1\),\(3sinx+4cosx<2\),\(2cos(2x+\cfrac{\pi}{3})<1\)
求函数\(y=\lg sinx+\sqrt{\cos2x+\frac{1}{2}}\)的定义域。
7.分段函数不等式
8.抽象函数不等式
9.排列数组合数不等式
\(\begin{cases} C_{10}^r2^{10-r} \ge C_{10}^{r-1}2^{11-r} \\ C_{10}^r2^{10-r}\ge C_{10}^{r+1}2^{9-r} \end{cases}\)
10.利用图像解不等式

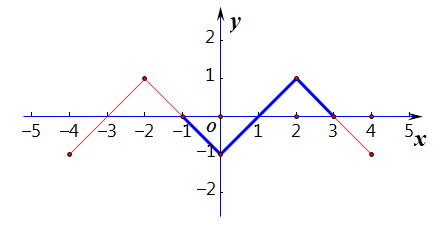
函数\(f(x)\)是周期为4的偶函数,当\(x\in[0,2]\)时,\(f(x)=x-1\),求不等式\(x\cdot f(x)>0\)在\([-1,3]\)上的解集。
法1:自己作图如右,读图即可解答,解集为\((-1,0)\cup(1,3)\);
法2:利用积的符号法则求解,原不等式等价于\(\begin{cases}x>0\\f(x)>0\end{cases}\)或\(\begin{cases}x<0\\f(x)<0\end{cases}\),
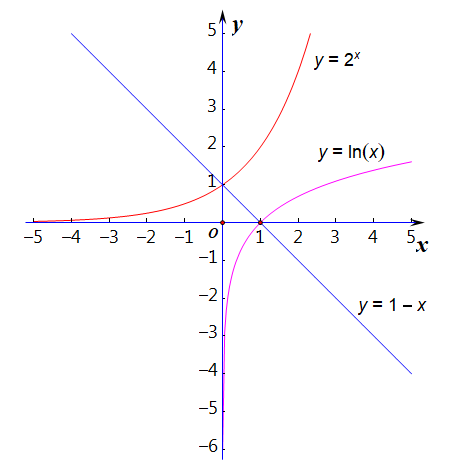

解关于\(x\)的不等式\(lnx>1-x\);
分析:你应该能感觉到,这个题目用我们平常的那种解法(代数解法)已经不能做出来了,因为它不是我们熟悉的那种代数不等式,而是超越不等式,这时候就需要我们借助图像来求解。
比如分别作出两个函数\(y=lnx\)和\(y=1-x\)的图像观察求解,如右图所示,解集为\((1,+\infty)\);
同类题目:解关于\(x\)的不等式\(2^x>1-x\);解集为\((0,+\infty)\);:解关于\(x\)的不等式\(log_2^x>\cfrac{2}{x}\);解集为\((2,+\infty)\);
补充:导函数的不等式。
11.综合运用(指能转化为解不等式的问题)
 \(\fbox{例1}\)
\(\fbox{例1}\)
函数\(f(x)=\cfrac{ln(x+3)}{\sqrt{1-2^x}}\)的定义域是\((-3,0)\).
 \(\fbox{例2}\)
\(\fbox{例2}\)
若函数\(f(x)=-x^2+2ax\)与\(g(x)=(a+1)^{1-x}\)在区间\([1,2]\)上都是减函数,求\(a\)的取值范围;
分析:函数\(f(x)\)开口向下,对称轴是\(x=a\),必须满足\(a\leq 1\);函数\(g(x)\)是指数型函数,必须满足\(a+1>0\)且\(a+1\neq 1\)且\(a+1>1\),求交集得到\(0<a\leq 1\).
 \(\fbox{例3}\)
\(\fbox{例3}\)
已知函数\(f(x)=\begin{cases}x^2+4x,&x\ge0\\4x-x^2,&x<0\end{cases}\),若\(f(2-a^2)>f(a)\),求实数\(a\)的取值范围。
分析:自行作图,结合分段函数\(f(x)\)的大致图像可知,\(f(x)\)在\(R\)上单调递增,故由\(f(2-a^2)>f(a)\),可直接脱掉符号\(f\),得到\(2-a^2>a\),解得\(-2<a<1\).
 \(\fbox{例4}\)
\(\fbox{例4}\)
已知函数\(f(x)=\cfrac{ax+b}{x}\cdot e^x,a、b\in R,a>0\),
(1).若函数\(f(x)\)在\(x=1\)处取到极值\(\cfrac{1}{e}\),试求函数\(f(x)\)的解析式和单调区间;
提示:\(f'(-1)=0,f(1)=\cfrac{1}{e}\),分别求得\(a-2b=0\)和\(a-b=1\),联立求得\(a=2,b=1\);则\(f(x)=\cfrac{2x+1}{x}\cdot e^x\);
求解单调区间,实质就是解不等式\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}>0\)和\(f'(x)=\cfrac{e^x(x+1)(2x-1)}{x^2}<0\),此时可以通过穿根法解分式不等式。\((-\infty,-1)和(\cfrac{1}{2},+\infty)\)单调递增;\((-1,0)和(0,\cfrac{1}{2})\)单调递减;
 \(\fbox{延伸阅读}\)
\(\fbox{延伸阅读}\)
1、穿根法的前世今生
2、三角不等式的解法
3、代数不等式,超越不等式
超越函数(\(Transcendental Functions\))是指变量之间的关系不能用有限次加、减、乘、除、乘方、开方运算表示的函数。如对数函数\(y=log_2^x\),反三角函数如\(y=arcsinx\),指数函数如\(y=2^x\),三角函数如\(y=sinx\)等就属于超越函数,它们属于初等函数中的初等超越函数。对数和指数函数即为超越函数的例子。超越函数这个名词通常被拿来描述三角函数。
非超越函数则称为代数函数。代数函数的例子包括多项式和平方根函数.
超越不等式和代数不等式
不等式两边的函数,如果都是代数函数,则称这个不等式为代数不等式;如果至少有一个是超越函数,则称这个不等式为超越不等式.前者可以划分为有理不等式(整式不等式和分式不等式)和无理不等式;后者包括指数不等式、对数不等式、三角不等式和反三角不等式等。