线性代数 --- 矩阵的QR分解，A=QR

矩阵的QR分解，格拉姆施密特过程的矩阵表示

首先先简单的回顾一下Gram-Schmidt正交化过程的核心思想。即，如何把一组线性无关的向量构造成一组标准正交向量，或者说，如何把一般的线性无关矩阵A变成标准正交矩阵Q。

给定一组线性无关的向量a,b,c，我们希望构造出一组相互垂直的单位向量q1,q2,q3。

$\mathbf{A=\begin{bmatrix} | & |& |\\ a& b&c \\ | & |& | \end{bmatrix}}$

第一步：

$\mathbf{A=a}$

得到这组正交向量中的第一个向量A，这就是说，我们令新的正交向量中的第一个向量A与向量a的方向相同，且大小相同。（这里我们用到了矩阵A中的向量a）

第二步：

$\mathbf{B=b-\frac{A^{T}b}{A^{T}A}A}$

现在，A已经确定了，第二个向量B必须垂直于A。我们令b减去b在A上的投影Pb，得到我们想要的第二个向量B。a,b与A,B不同，但都在同一个平面内。

注意：向量B一定不等于0，因为B是b在a(A)上的投影/分量之外的分量e。如果a,b线性相关，则b在a上投影后再无其他分量。这与a,b线性无关这一事实相左。(这里我们用到了矩阵A中的向量b)

第三步：

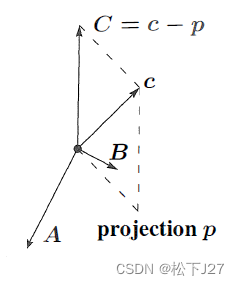
$\mathbf{C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B}$

现在我们基于c去找第三个向量C，C必须垂直于A,B所张成的平面，即A,B所在的子空间。我们令c减去c在这个平面上的投影Pc(注意：c在A,B所构建的子空间上的投影，等于向量c分别在A和B上的投影之和),得到向量C。（这里我们用到了矩阵A中的向量c）

如果矩阵A中还有第四个，第五个向量d,e,f,g......的话，我们只需在这个基础上重复上述过程就能找到新的正交向量D,E,F,G......。

第四步：

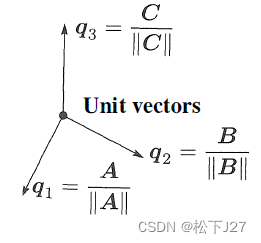
$\mathbf{q_{1}=\frac{A}{\left \| A \right \|},q_{2}=\frac{B}{\left \| B \right \|},q_{3}=\frac{C}{\left \| C \right \|}}$

当我们把前面的正交向量A,B,C全部找完以后，让他们分别除以各自的长度，最终得到一组标准正交向量q1,q2,q3。这最后一步被称为向量的归一化。

下面给出了gram-schmidt正交过程的一个实例，已知一组线性无关的向量a,b,c：

$\mathbf{a=\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix} \; b=\begin{bmatrix} 2\\ 0\\ -2\end{bmatrix} \; b=\begin{bmatrix} 3\\ -3\\ 3 \end{bmatrix}}$

第一步：令A=a得到

$\mathbf{A=a=\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix}}$

第二步：从b中减去b在A上的投影得到

$\mathbf{B=b-\frac{A^{T}b}{A^{T}A}A=b-\frac{2}{2}A=\begin{bmatrix} 1\\ 1\\ -2 \end{bmatrix}}$

第三步：从c中减去c在AB平面上的投影得到

$\mathbf{C=c-\frac{A^{T}c}{A^{T}A}A-\frac{B^{T}c}{B^{T}B}B=c-\frac{6}{2}A+\frac{6}{6}B=\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}}$

第四步：归一化

$\mathbf{\left \| A \right \|=\sqrt{A^{T}A}=\sqrt{2}, \; \left \| B \right \|=\sqrt{B^{T}B}=\sqrt{6}, \; \left \| C \right \|=\sqrt{C^{T}C}=\sqrt{3}}$

$\mathbf{q_{1}=\frac{A}{\left \| A \right \|}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1\\ -1\\ 0 \end{bmatrix}\; q_{2}=\frac{B}{\left \| B \right \|}=\frac{1}{\sqrt{6}}\begin{bmatrix} 1\\ 1\\ -2 \end{bmatrix}\; q_{3}=\frac{C}{\left \| C \right \|}=\frac{1}{\sqrt{3}}\begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}\;}$

一般而言，A,B,C往往会含有分数。而几乎所有的q1,q2,q3都会包含根号。

结论：

任何一个线性无关的向量组a1,a2,...,an都可以用Gram-schmidt正交化过程转化成一个正交向量组A1,A2,...,An：首先令A1=a1,然后使每个Ai与前面的A1,A2,...,Ai-1均正交

$\mathbf{A_{i}=a_{i}-\frac{{A_{1}}^{T}a_{i}}{{A_{1}}^{T}A_{1}}A_{1}-\frac{{A_{2}}^{T}a_{i}}{{A_{2}}^{T}A_{2}}A_{2}-\cdots -\frac{{A_{i-1}}^{T}a_{i}}{{A_{i-1}}^{T}A_{i-1}}A_{i-1}}$

对每个i而言，由原来a1,a2,...,ai所张成的子空间也由A1,A2,...,Ai所张成。对所有Ai归一化后最终得到的向量组qi是一组标准正交向量

$\mathbf{q_{i}=\frac{A_{i}}{\left \| A_{i} \right \|},(i=1,2,...,n)}$

QR分解

正如我们在高斯消元法看到的，通过对矩阵A的一系列消元，最终的得到了消元矩阵U。事后，我把每一步的消元过程记录下来并以矩阵的形式表示得到了上三角矩阵L，得到了矩阵A的LU分解。Gram-schmidt正交化过程也相仿，通过一系列计算把矩阵A变成了标准正交矩阵Q，应当也能找到一个方法把这个过程记录下来，并用矩阵的形式表示。

LU分解的精髓在于，通过矩阵L我们能把计算结果U还原回去，这里也一样。要知道怎么把Gram-Schmidt正交化最终得到的结果q1,q2,q3还原回去？

根据我们刚才的例子，有：

$\left\{\begin{matrix} A=a\\B=b-A\\ C=c-3A+B\end{matrix}\right. \; and\; \left\{\begin{matrix} q_{1}=\frac{A}{\left \| A \right \|}=\frac{1}{\sqrt{2}}A\\q_{2}=\frac{B}{\left \| B \right \|}=\frac{1}{\sqrt{6}}B\\ q_{3}=\frac{C}{\left \| C \right \|}=\frac{1}{\sqrt{3}}C\end{matrix}\right.$

如果用q1,q2,q3来表示a,b,c则有如下方程组：

$\left\{\begin{matrix} a=A\\b=A+B\\ c=3A-B+C\end{matrix}\right. \; and\; \left\{\begin{matrix} A=\sqrt{2}q_{1} \\B=\sqrt{6}q_{2}\\ C=\sqrt{3}q_{3}\end{matrix}\right.$

结合上述左右两个方程组，最终得到如下方程组：

$\left\{\begin{matrix} a=\sqrt{2}q_{1} \\b= \sqrt{2}q_{1}+ \sqrt{6}q_{2}\\ c=3\sqrt{2}q_{1} -\sqrt{6}q_{2}+\sqrt{3}q_{3} \end{matrix}\right.$

（记作：QR方程组）

上面的这个用q1,q2,q3的线性组合来表示a,b,c的方程组用矩阵的形式可写作：

$A=\begin{bmatrix} | & | &| \\ a & b &c \\ | & | &| \end{bmatrix}= \begin{bmatrix} | & | &| \\ q_{1} & q_{2} &q_{3} \\ | & | &| \end{bmatrix} \begin{bmatrix} \sqrt{2}&\sqrt{2} &3\sqrt{2} \\0 &\sqrt{6} &-\sqrt{6} \\ 0& 0&\sqrt{3} \end{bmatrix}=QR$

原来的矩阵A被分解成了一个标准正交矩阵Q和一个上三角矩阵R的乘积，得到了线性代数中和LU分解同样重要，同样有用的另一个分解，QR分解。

矩阵R对角线上的元素 $\sqrt{2},\sqrt{6},\sqrt{3}$ 正好是正交向量A,B,C的长度。现在我们再回过头去看看上面的QR方程组，可以看到QR方程组把a,b,c这三个矩阵A中的列向量表示成了q1,q2,q3的线性组合。且，a是q1的线性组合(相应的权重系数在R的第一列)，不涉及q2,q3。b是q1,q2的线性组合(相应的权重系数在R的第二列)，不涉及q3。只有c是q1,q2,q3的线性组合(相应的权重系数在R的第三列)。这也是为什么R是一个上三角矩阵的原因。又因为R对角线上的元素都是正的，因而是可逆的，由此，得出了关于QR分解的重要结论：

任何由一组线性无关的列向量所组成的矩阵A都可以分解为A=QR的形式。Q的列向量一组标准正交向量，R是一个可逆的上三角矩阵。如果原矩阵A是方阵，则矩阵Q和矩阵R也是方阵，同时方阵矩阵Q也顺理成章的成为了标准正交矩阵。

QR分解的一般形式：

在之前的例子中，我基于一个实例得到了A的QR分解。并且发现向量a,b,c是单位正交向量q1,q2,q3的线性组合。现在我们已经发现了a,b,c与q1,q2,q3之间的联系，只需重新用q1,q2,q3来表示a,b,c(即：把原始向量中的a,b,c用q1,q2,q3的线性组合来表示)就能找到矩阵A与矩阵Q之间的联系---矩阵R。

第一步：

首先，我们知道合成a与q1方向相同(a与q2,q3无关)，且a在q1上的投影就是a，建立了q1与a的关系

$\mathbf{a=\frac{q_{1}^{T}a}{q_{1}^{T}q_{1}}q_{1}}$

又因为，我们已知q1为单位向量，所以上式可简化为：

$\mathbf{a=\frac{q_{1}^{T}a}{1}q_{1}=(q_{1}^{T}a)q_{1}}$

第二步：b等于b在q1,q2上的投影之和(与q3无关)

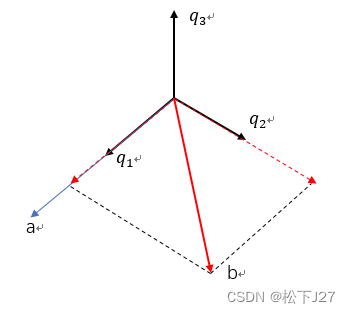
$\mathbf{b=\frac{q_{1}^{T}b}{q_{1}^{T}q_{1}}q_{1}+\frac{q_{2}^{T}b}{q_{2}^{T}q_{2}}q_{2}}$

根据q1,q2的长度为1，得到：

$\mathbf{b=(q_{1}^{T}b)q_{1}+(q_{2}^{T}b)q_{2}}$

第三步：c等于c在q1,q2,q3这三个向量上的投影之和

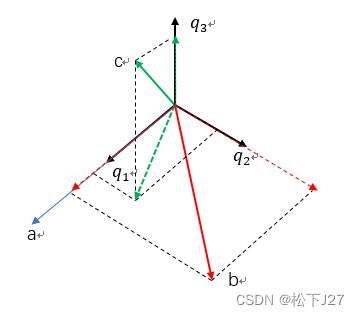
$\mathbf{c=\frac{q_{1}^{T}c}{q_{1}^{T}q_{1}}q_{1}+\frac{q_{2}^{T}c}{q_{2}^{T}q_{2}}q_{2}+\frac{q_{3}^{T}c}{q_{3}^{T}q_{3}}q_{3}}$

根据q1,q2,q3的长度都为1，得到：

$\mathbf{c=(q_{1}^{T}c)q_{1}+(q_{2}^{T}c)q_{2}+(q_{3}^{T}c)q_{3}}$

至此，已经得到了a,b,c基于q1,q2,q3的线性组合，用方程表示如下：

$\left\{\begin{matrix}\mathbf{a=(q_{1}^{T}a)q_{1}}\\\mathbf{b=(q_{1}^{T}b)q_{1}+(q_{2}^{T}b)q_{2}}\\ \mathbf{c=(q_{1}^{T}c)q_{1}+(q_{2}^{T}c)q_{2}+(q_{3}^{T}c)q_{3}}\end{matrix}\right.$

将上述方程写成矩阵的形式，即得到了著名的QR分解的矩阵表达式：

$\mathbf{A=\begin{bmatrix} | & | &| \\ a & b &c \\ | & | &| \end{bmatrix}= \begin{bmatrix} | & | &| \\ q_{1} & q_{2} &q_{3} \\ | & | &| \end{bmatrix} \begin{bmatrix} q_{1}^{T}a&q_{1}^{T}b &q_{1}^{T}c \\0 &q_{2}^{T}b &q_{2}^{T}c\\ 0& 0&q_{3}^{T}c \end{bmatrix}=QR}$