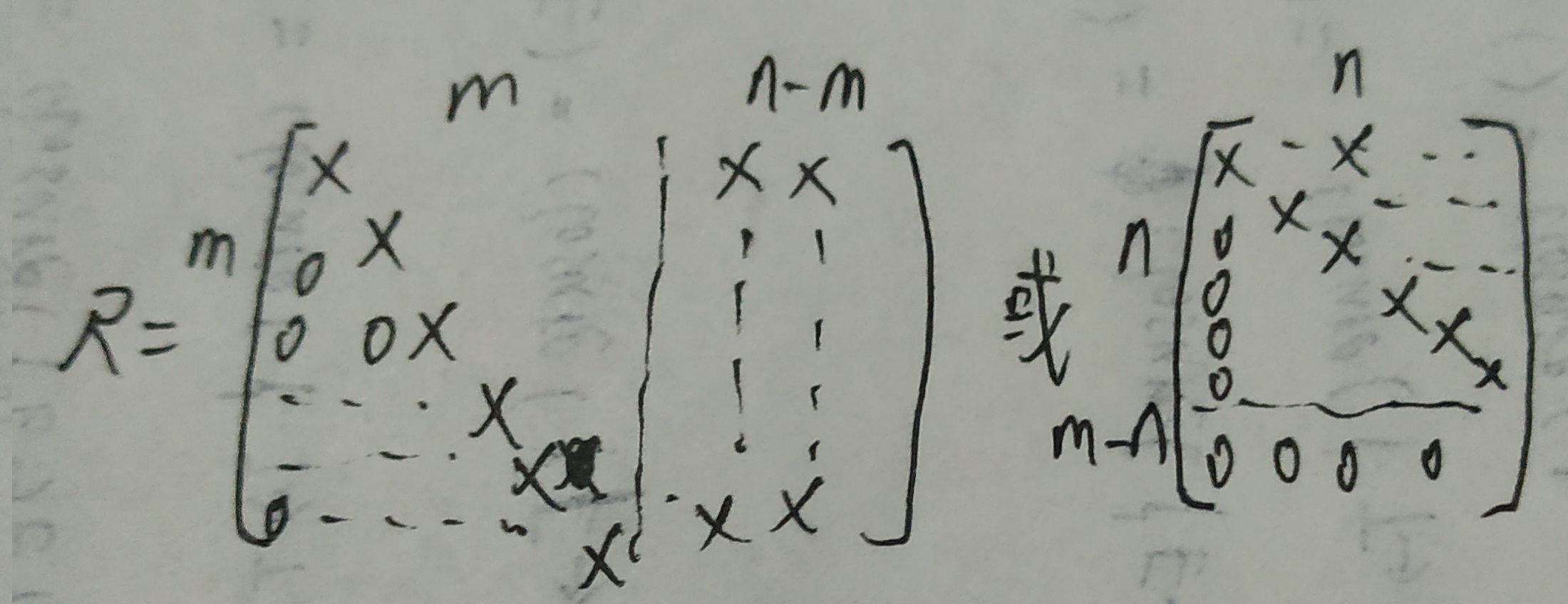矩阵的QR分解求解线性方程组

一.QR分解概念

QR分解指的把矩阵分解成一个正交矩阵与一个上三角矩阵的积。
正交矩阵：如果n阶方阵A满足$A{A}^T=A^{T}A=E(即A^{-1}=A^T)$,那么称A为正交矩阵。
上三角矩阵:

$A=QR$，Q是正交矩阵，R是上三角矩阵。

二.使用HouseHolder变换来实现QR分解

1.共轭转置

对于一个矩阵$A$，它的共轭转置我们记为$A^{\ast }$,他们之间满足如下关系:
$(A^{\ast }{)}_{i,j}=\overline{A_{j,i}}$,当然也有其他等价形式:
$A^{\ast }=\overline{A^T}=(\overline{A}{)}^T$,那么我们这里给出一个例子:
$$A=\left[\begin{array}{cc}3+i& 5\\ 2-2i& i\end{array}\right]$$
$$A^{\ast }=\left[\begin{array}{cc}3-i& 2+2i\\ 5& -i\end{array}\right]$$

2.HouseHolder变换实现QR分解

对于任意的一个模长为1的列向量w,我们构造豪斯霍尔德矩阵:
$H=I-2w{w}^T$,其中$I$为单位矩阵。这里$w^T$没使用共轭转置，是因为目前我们先只考虑实数的形式。从这个形式我们可以得到下面一般性的结论"

$H^T=H$
$H\ast H=I$

这说明$H$是一个对称正交阵。实际上H也是一个反射矩阵。下面我们来说说为什么？
首先介绍超平面，指和$w$垂直(即乘积为0)的所有向量$x$组成的平面。
记作:

S = { x ∣ w T x = 0 , ∀ x ϵ R n } S=\{x|w^Tx=0, \forall x\epsilon R^n \} S={ x∣wTx=0,∀xϵRn}

基于这样的定义，我们很容易明白，对于一个任意的向量$zϵR^n$,向S与w张成的这个空间上一定可以进行唯一的分解。
记作$z=x+y,x$在超平面$S$上，而$y=\alpha w,\alpha$是一个实数。
那么有:

$Hz=x+(I-2w{w}^T)\ast y=x+y-2\alpha w(w^{T}w)=x-y$
这就很明显了，$H$相当于将$z$按照S平面进行了依次反射对称。这就是H为反射矩阵的由来。

这里我们介绍一个定理：

对于任意的模相等的向量$x,y$,我们都可以找到一个反射矩阵$H$，使得$Hx=y,H=I-2w{w}^T,w=\frac{x-y}{||x-y||}$
这个定理我们的用法是这样的，给定一个向量$x$,它的模长是$l$,那么我们可以找到$H$使得$Hx=[\pm l,0,0,...,0{]}^T$

3.QR分解解线性方程组实现代码

//
int DSPF_dp_qrd_solver(const int Nrows,const int Ncols,double *restrict Q,double *restrict R,double *restrict b,double *restrict y,double *restrict x) {
    
    

  short row,col,loop_cnt;
  double sum;
  double xx,yy;

  _nassert(Nrows>0);
  _nassert(Ncols>0);
  _nassert((int)Q % 8 == 0);
  _nassert((int)R % 8 == 0);
  _nassert((int)b % 8 == 0);
  _nassert((int)y % 8 == 0);
  _nassert((int)x % 8 == 0);

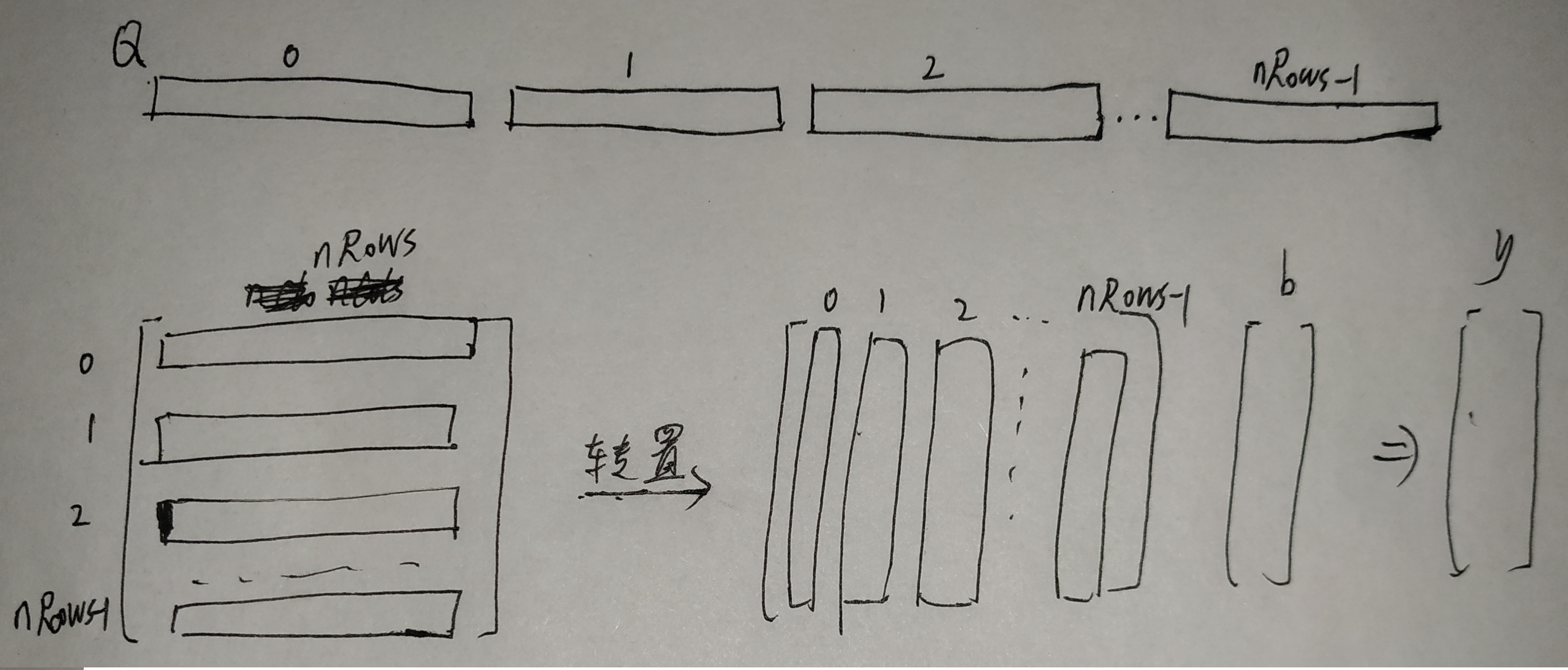
  /* generate y=Q'*b 见第一张图*/
#pragma MUST_ITERATE(1,,)
  for (row=0;row<Nrows;row++) {
    
    
	sum=0.0;
#pragma MUST_ITERATE(1,,)
	for (col=0;col<Nrows;col++) {
    
    
	  sum+=Q[row+col*Nrows]*b[col];
	} 
	y[row]=sum;
  }

  /* use backward substitution to solve x=inv(R)*y 见第二张图*/
  if (Nrows>=Ncols) loop_cnt=Ncols;
  else              loop_cnt=Nrows;
  memset(x,0,sizeof(double)*Ncols);
#pragma MUST_ITERATE(1,,)
  for (row=loop_cnt-1;row>=0;row--) {
    
    
	sum=0.0;
	xx=R[row+row*Ncols];
	yy=_rcpdp(xx);//yy是xx的倒数
	yy=yy*(2.0-xx*yy);
	yy=yy*(2.0-xx*yy);
	yy=yy*(2.0-xx*yy);
#pragma MUST_ITERATE(1,,)
	//模拟高斯消元的方法 
	for (col=row+1;col<loop_cnt;col++) {
    
    
	  sum+=R[col+row*Ncols]*x[col];//如果有无穷多组解时最下面的几个就赋值为0
	}
	x[row]=(y[row]-sum)*yy;
  }
  return 0;
}