空间直线到平面上的交点的计算证明及其源码

目的：最近写C++代码，遇到一些基础的算法。需要空间直线和平面的交点。

直线的向量表达：$L:\overrightarrow{r}=\overrightarrow{P_0}+t\overrightarrow{N_0}$；其中$\overrightarrow{P_0}=\left(\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right)$, $\overrightarrow{N_0}=\left(\begin{array}{c}{n}_x^0\\ n_y^0\\ n_z^0\end{array}\right)$
平面的向量表达：$\pi :{\overrightarrow{N_1}}^T\cdot X+d_1=0$；其中$\overrightarrow{N_1}=\left(\begin{array}{c}{n}_x^1\\ n_y^1\\ n_z^1\end{array}\right)$,$d$为标量。

对于直线到平面的交点它分为三种情况：
1）在平面上
2）平行平面
3）和平面相交
图示如下：

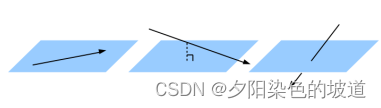
左图和中间图可以看到，它和平面没有交点。因此需要判断直线是否和平面相交。在传统的空间中，平面和直线平面的话，直线和平面的发向量是垂直的。因此可以通过计算$\overrightarrow{N_0}$和 $\overrightarrow{N_1}$之间的夹角。如果它是垂直表面直线和平面平行。
$cos(\theta )->{\overrightarrow{N_0}}^T\cdot \overrightarrow{N_1}$
如果它接近于0表示它平行。

下面将介绍相交的情况
如果平面和直线相交，对于直线来说，只需要计算$t$即可。
$L:\overrightarrow{r}=\overrightarrow{P_0}+t\overrightarrow{N_0}$带入公式$\pi :{\overrightarrow{N_1}}^T\cdot X+d_1=0$得到如下：
$$\begin{gathered} {\overrightarrow{N_1}}^T\cdot (\overrightarrow{P_0}+t\overrightarrow{N_0})+d_1=0 \\ =>{\overrightarrow{N_1}}^T\cdot \overrightarrow{P_0}+t{\overrightarrow{N_1}}^T\cdot \overrightarrow{N_0}+d_1=0 \\ t=(-d_1-{\overrightarrow{N_1}}^T\cdot \overrightarrow{P_0})/{\overrightarrow{N_1}}^T\cdot \overrightarrow{N_0} \end{gathered}$$
因为向量$\overrightarrow{P_0}$,$\overrightarrow{N_0}$,$\overrightarrow{N_1}$都是已知，因此可以求的$t=t_n$。
带入得到
$$\overrightarrow{r_n}=\overrightarrow{P_0}+t_n\overrightarrow{N_0}$$

基于上述的公式，源码如下：

bool LineRayToPlanePnt(Eigen::Vector3f& o_orign, Eigen::Vector3f& o_dir, Eigen::Vector4f& fn, Eigen::Vector3f& inter_pnt)
	{
    
    
		Eigen::Vector3f N = Eigen::Vector3f(fn[0], fn[1], fn[2]);
		float D = fn[3];
		if (std::abs(o_dir.dot(N)) < 1e-8)
		{
    
    
			return false;
		}
		float t = -(o_orign.dot(N) + D) / (o_dir.dot(N));
		inter_pnt = o_orign + t*o_dir;
	}