空间顶点到直线的距离计算及其源码

目的：最近研究项目遇到点到直线的距离，在空间几何中，非常重要的一个基础的算法，因此记录。

直线的向量表达：$L:\overrightarrow{r}=\overrightarrow{P_0}+t\overrightarrow{N_0}$；其中$\overrightarrow{P_0}=\left(\begin{array}{c}{x}_0\\ y_0\\ z_0\end{array}\right)$, $\overrightarrow{N_0}=\left(\begin{array}{c}{n}_x^0\\ n_y^0\\ n_z^0\end{array}\right)$
顶点的向量表达：$\overrightarrow{P}:\left(\begin{array}{c}{x}_1\\ y_1\\ z_1\end{array}\right)$。

顶点到直线的距离有多种方法，先介绍一个非常简单的方法，它基于向量表达得到。

1）方法一：
假设顶点$\overrightarrow{P}$投影到直线上得到$\overrightarrow{P^{\prime }}$,根据点到直线的距离定义，$|\overrightarrow{P{P}^{\prime }}|$为顶点$\overrightarrow{P}$到直线$L$的距离。如下图：

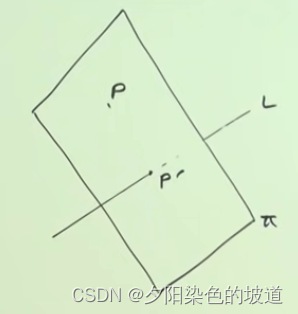
下面将介绍计算过程：
因为顶点$\overrightarrow{P^{\prime }}$在直线上，它可以表达为：$\overrightarrow{P^{\prime }}=\overrightarrow{P_0}+t^{\prime }\overrightarrow{N_0}$，所以：
$$\overrightarrow{P{P}^{\prime }}=(\overrightarrow{P_0}+t^{\prime }\overrightarrow{N_0})-\overrightarrow{P}$$

因为$\overrightarrow{P{P}^{\prime }}$和直线$L$垂直，可以得到：${\overrightarrow{P{P}^{\prime }}}^T\cdot \overrightarrow{N_0}=0$

$$\begin{gathered} {\overrightarrow{P{P}^{\prime }}}^T\cdot \overrightarrow{N_0}=0 \\ =>(\overrightarrow{P_0}+t^{\prime }\overrightarrow{N_0}-\overrightarrow{P}{)}^T\cdot \overrightarrow{N_0}=0 \\ =>(t^{\prime }\overrightarrow{N_0}+\overrightarrow{P_0}-\overrightarrow{P}{)}^T\cdot \overrightarrow{N_0}=0 \\ =>t^{\prime }{\overrightarrow{N_0}}^T\cdot \overrightarrow{N_0}=({\overrightarrow{P}}^T-{\overrightarrow{P_0}}^T)\cdot \overrightarrow{N_0} \\ =>t^{\prime }=({\overrightarrow{P}}^T-{\overrightarrow{P_0}}^T)\cdot \overrightarrow{N_0}/({\overrightarrow{N_0}}^T\cdot \overrightarrow{N_0}) \end{gathered}$$

通过$t^{\prime }$计算$P^{\prime }=\overrightarrow{P_0}+t^{\prime }\overrightarrow{N_0}$

$$d=|\overrightarrow{P{P}^{\prime }}|=|(\overrightarrow{P_0}+t^{\prime }\overrightarrow{N_0})-\overrightarrow{P}|$$

得到点到直线的距离$d$。C++代码如下：

#include<iostream>
#include<Eigen/Eigen>
#include <vector>

void ComputePntProj2Line3D(Eigen::Vector3d& lpnt, Eigen::Vector3d& ldir, Eigen::Vector3d& pnt, Eigen::Vector3d& proj)
{
    
    
    //计算pi平面
    //std::cerr << "lpnt: "<< lpnt.transpose() <<std::endl;
    //std::cerr << "ldir: "<< ldir.transpose() <<std::endl;
    //std::cerr << "pnt: "<< pnt.transpose() <<std::endl;
    double t = (pnt.dot(ldir) - lpnt.dot(ldir)) / ldir.squaredNorm();
    //std::cerr <<"t: " << t <<std::endl;
    proj = t * ldir + lpnt; 
}
double ComputePnt2Line3D(Eigen::Vector3d& lpnt, Eigen::Vector3d& ldir, Eigen::Vector3d& pnt)
{
    
    
    //start to compute dist between pnt and line(lpnt, ldir)
    Eigen::Vector3d proj;
    ComputePntProj2Line3D(lpnt,  ldir,  pnt,  proj);
    //std::cerr << "proj: "<< proj.transpose() <<std::endl;
    double d = (proj - pnt).norm();
    return d;
}

int main(int argc, char** argv)
{
    
    
    Eigen::Vector3d lp,ld;
    ld = Eigen::Vector3d(3.0, 1.0, 1.0);
    lp = Eigen::Vector3d(-4.0, -5.0, -1.0);
    Eigen::Vector3d p;
    p = Eigen::Vector3d(-6.0, 1.0, 21.0);
    double dist = ComputePnt2Line3D(lp, ld, p);
    std::cerr <<"dist: " << dist <<std::endl;
    return 0;
}

代码测试：

2）方法二：(后续添加)

扫描二维码关注公众号，回复： 15755177 查看本文章