Python机器学习入门--线性回归学习笔记

---

机器学习简介

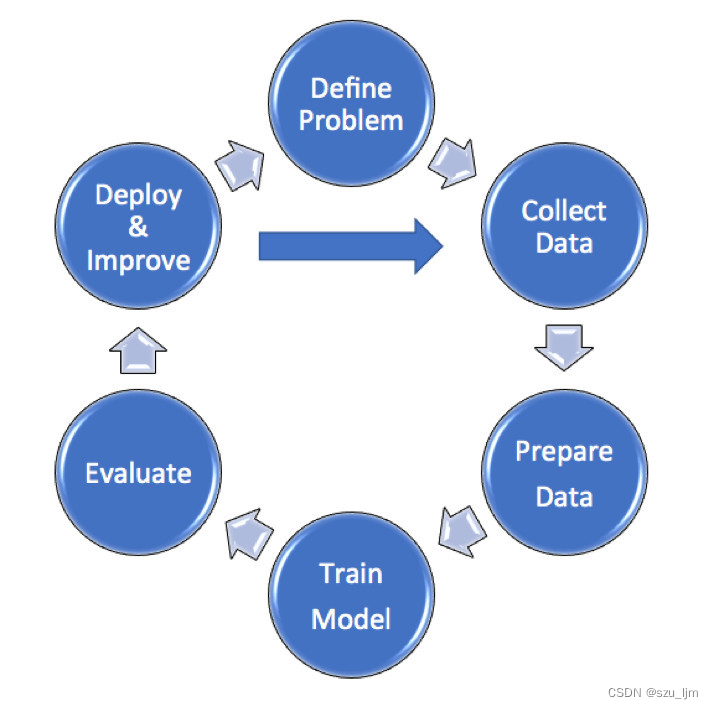
机器学习是一类算法的总称，这些算法企图从大量历史数据中挖掘出其中隐含的规律，并用于预测或者分类。从数学角度来说，机器学习可以看作是寻找一个函数，输入是样本数据，输出是期望的结果，只是这个函数过于复杂，以至于不太方便形式化表达。需要注意的是，机器学习的目标是使学到的函数很好地适用于“新样本”，而不仅仅是在训练样本上表现很好，即希望该模型有很强泛化能力。

1、按任务类型分，机器学习模型可以分为回归模型、分类模型和结构化学习模型。回归模型又叫预测模型，输出是数值；分类模型又分为二分类模型和多分类模型，常见的二分类问题有垃圾邮件过滤，常见的多分类问题有文档自动归类；结构化学习模型的输出不再是一个固定长度的值，如图片语义分析，输出是图片的文字描述。

2、从方法的角度分，可以分为线性模型和非线性模型，线性模型较为简单，但作用不可忽视，线性模型是非线性模型的基础，很多非线性模型都是在线性模型的基础上变换而来的。非线性模型又可以分为传统机器学习模型，如SVM，KNN，决策树等，和深度学习模型。

3、按照学习理论分，机器学习模型可以分为有监督学习，半监督学习，无监督学习，迁移学习和强化学习。当训练样本带有标签时是有监督学习；训练样本部分有标签，部分无标签时是半监督学习；训练样本全部无标签时是无监督学习。迁移学习就是就是把已经训练好的模型参数迁移到新的模型上以帮助新模型训练。强化学习是一个学习最优策略，可以让本体在特定环境中，根据当前状态，做出行动，从而获得最大回报。强化学习和有监督学习最大的不同是，每次的决定没有对与错，而是希望获得最多的累计奖励。

---

一、线性回归的数学原理

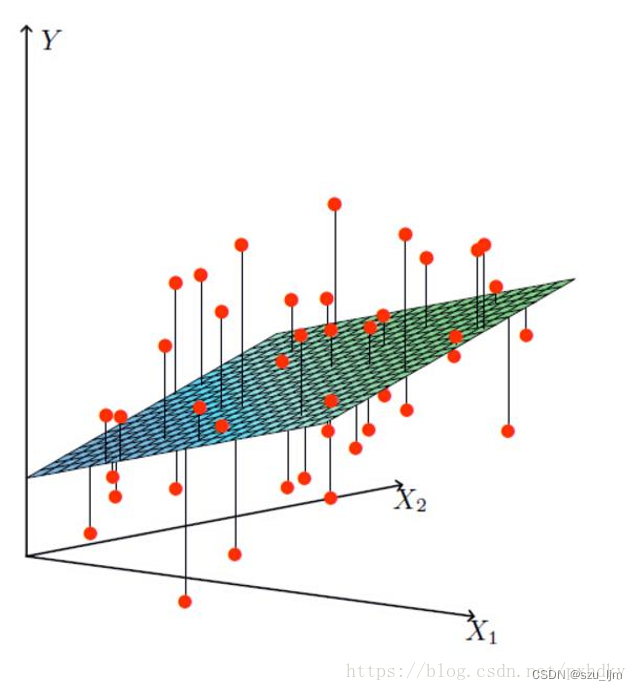
线性回归的概念大概是我们在学高中数学首次接触到的，老师通常会抛出一个问题，例如给你某个股票随时间变化的价值，大多是离散型数据，让你拟合一条直线来预测未来的股票价值走向，当时老师教的方法是用最小二乘法来求该拟合直线的方程，今天就更加详细的来学习线性回归中的数学原理

1. 标签和特征

机器学习里面有两个重要的名词：标签和特征。

特征表示对信息的维度进行一个分类，人们在认识一个事物的过程中总是善于提取该事物的特征，用不同的特征对该事物进行一个认知衡量，同样机器在学习一个事物时也应该对不同的特征的数据进行学习归纳，这样才能逐渐拥有人类的智能。

标签是有监督学习中十分重要的数据，标签好比在人认知事物后下的一种归纳结论，机器学习的最终目的是通过对数据的挖掘归纳不断逼近标签值，寻找物理世界中一种普遍存在的规律。

2. 残差和概率分布

假设我们想预测银行贷款的额度随年龄和工资的相关趋势变化，其实就是要根据训练集的数据，拟合一个最优的平面来使观测值和真实值最接近，这个例子需要年龄和工资两个特征的数据集

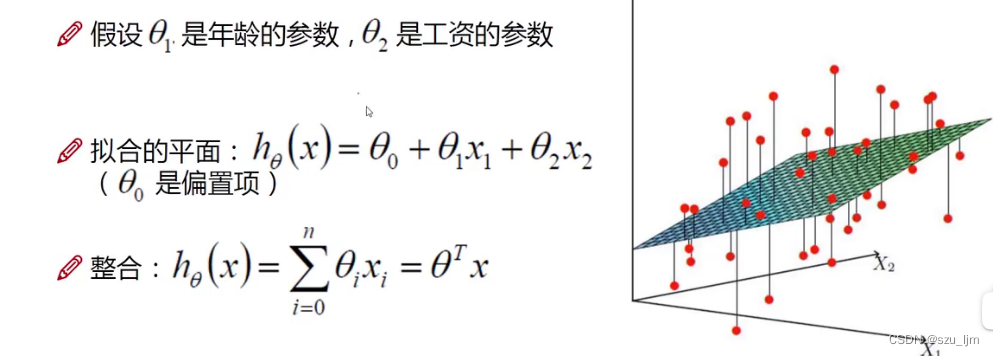
三个参数${\theta }_i,i=0,1,2$是我们求解的目标函数，在机器学习中我们将这三个参数称为权重，即对不同特征的一个衡量指标，在数学上这三个参数就是用来表征整个平面的倾斜方向。我们利用矩阵乘法进行简化最后得到的拟合平面方程就是
$$h_{\theta }(x)={\theta }^{T}x$$
注意这里的$\theta$是关于三个参数的矩阵，$x$是矩阵数据集，其中矩阵数据集最开始要抽出一列全部填充为1，方便矩阵运算

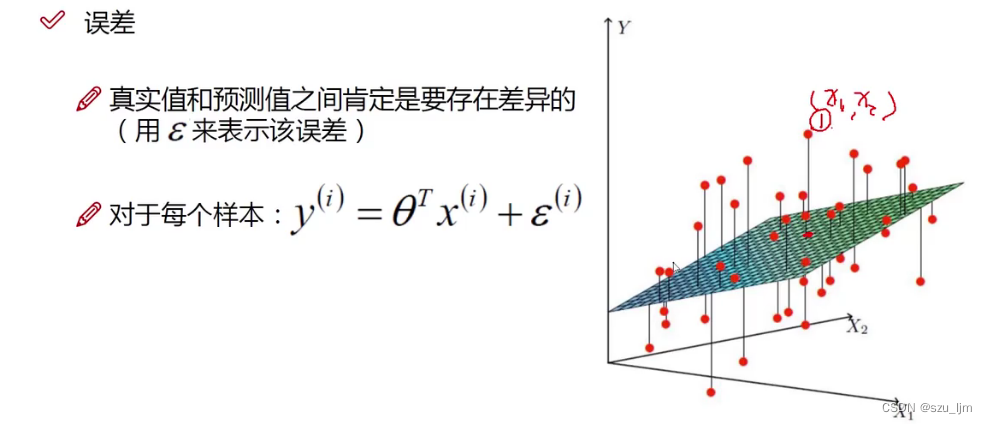
残差在数学上的定义是真实值和观测值的差值，即训练数据集中的 $y$ 值和训练结果的预测值 $\hat{y}$ 的差值，残差一般用 ${\epsilon }^{(i)}$ 来表示
$${\epsilon }^{(i)}=y^{(i)}-{\theta }^{T}x$$

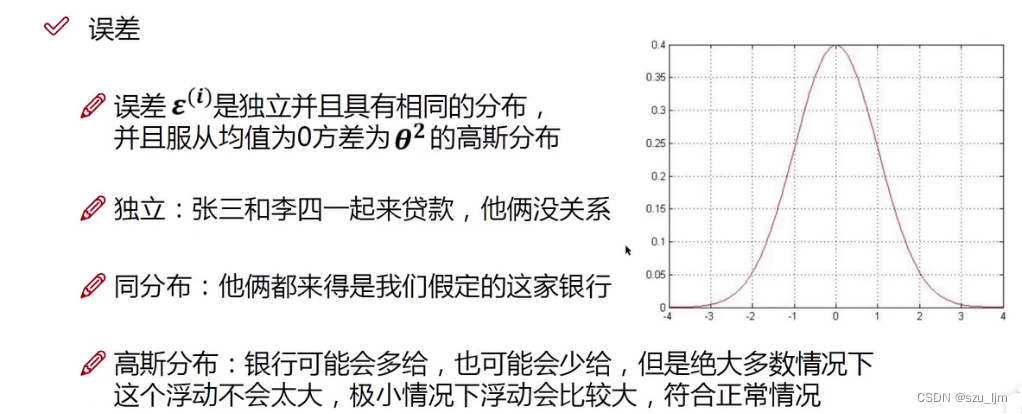
在统计学中，残差 ${\epsilon }^{(i)}$ 遵循标准正态分布，这也十分符合事实。在物理世界中，越偏离正常值和平均值的事件发生的概率就越小，越接近正常值和平均值的事件发生的概率就越大

标准的正态分布的表达式$$p({\epsilon }^{(i)})=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{({\epsilon }^{(i){)}^2}}{-2{\sigma }^2}}$$
将残差的表达式代入即可得到$$p({\epsilon }^{(i)})=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{(y^{(i)}-{\theta }^{T}x{)}^2}{-2{\sigma }^2}}$$
接下来就可以需要用似然函数对残差的概率分布进行处理

3. 似然函数

最大似然估计和贝叶斯分析是机器学习中十分重要的两个方法，但它们有着本质的区别。想象一个篮球比赛的绝杀场景，假设有几位绝杀人选，贝叶斯是想要描述的是这几个人选中每个人绝杀的概率，而最大似然想要描述的是在已知有人绝杀的情况下，最可能投出绝杀球的人是谁。区别就在于贝叶斯要求解事件未发生的情况下它的概率，这需要用到先验概率；而最大似然估计想要在事件已发生的情况下，求解某个参数下的状态能带来最大的可能性

似然函数 $L(\theta )$ 是联合概率的乘积，就是在某个参数 $\theta$ 下观测值和真实值接近的概率的乘积。为了求具体的哪个参数 $\theta$ 才能使这个接近的概率最大 ，需要对参数 $\theta$ 求偏导。为了方便求偏导的计算，我们先要将似然函数转化为对数似然函数。

4. 矩阵求偏导

为了求得似然函数取最大值的参数 $\theta$ 的值，我们分析一下展开后的对数似然函数，常数不影响结果可以直接省略，只剩下最小二乘法的表达式，这就是最小二乘法的数学原理推导。我们希望的是 $J(\theta )$ 越大越好，因为这样残差才能尽可能小，所以用 $J(\theta )$ 对 $\theta$ 求偏导来求得取极值时驻点 $\theta$ 的值。

因为 $\theta ,x,y$都是矩阵，所以其实是对矩阵求偏导使偏导等于0，最后就可以得到参数 $\theta$ 的驻点值

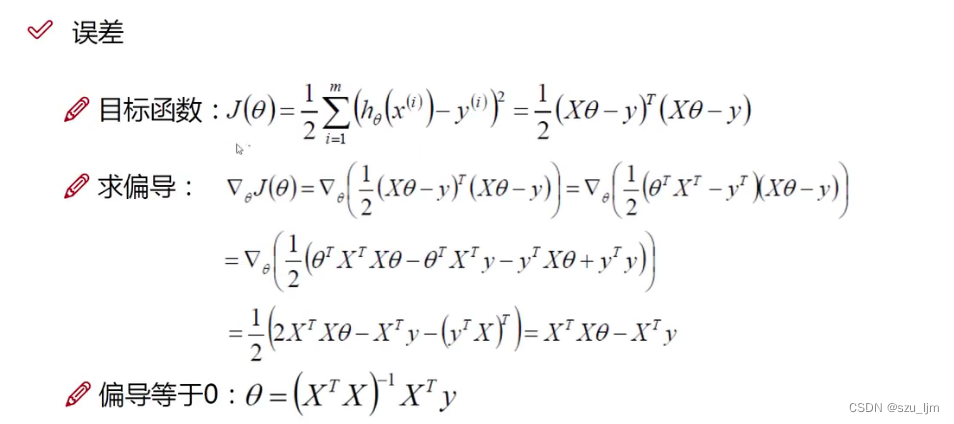
二、机器学习中的梯度下降

在机器学习中实现线性回归的操作中并非完全按照数学原理的推导来，我们希望机器在学习的过程中自己找到最优的驻点 $\theta$ ，所以我们并不是直接把最优解 $\theta =(X^{T}X{)}^{-1}{X}^{T}y$ 告诉机器，而是希望它自己通过归纳学习来逼近最优解，这时候就要用到机器学习中常见的方法 - - 梯度下降

梯度下降就像你爬山时想要从山上某个位置来到山谷最低点，你的预期是到达山谷最低点所需的时间最短，所以你要找到一个比较大的坡度，这样你才能沿山势下降的快，但你不能沿一个陡坡走一大步，那很容易跌倒，所以适当的步幅和坡度很重要

梯度下降中常见有批量梯度下降和随机梯度下降，批量梯度下降虽然收敛速度慢但是最容易得到驻点值，随机梯度下降虽然收敛速度快但是容易出现偏离驻点的情况，线性回归中我们采用小批量梯度下降的方法来更新参数逼近驻点，即通过对目标函数求偏导，然后拿所有样本的平均梯度来来更新参数 $\theta$

三、python实现线性回归

Python实现线性回归需要用到numpy, pandas, matplotlib三个库，当然也可以直接用keras和pytorch的模型调参更快捷，但我们为了理解原理将线性回归中的数学原理用代码模拟了一边，主要是训练和预测两大块，训练包括数据预处理，矩阵内积求 $J(\theta )$ 模块 ，梯度下降模块，损失函数模块。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt



class LinearRegression:
    def __init__(self, data, labels, features_mean=0, features_deviation=0, normalize_data=0):

        self.data = data
        self.labels = labels
        self.features_mean = features_mean
        self.features_deviation = features_deviation
        self.normalize_data = normalize_data
        num_features = self.data.shape[0]
        self.theta = np.ones((num_features, 1))

    def train(self, alpha, num_iterations = 500): 
        cost_history = self.gradient_descent(alpha, num_iterations)
        return self.theta, cost_history


    def gradient_descent(self, alpha, num_iterations):
        cost_history = []
        for _ in range(num_iterations):
            self.gradient_step(alpha)
            cost_history.append(self.cost_function(self.data, self.theta))
            print(cost_history)
        return cost_history


    def gradient_step(self, alpha):
        num_examples = self.data.shape[0]
        predictions = LinearRegression.hypothesis(self.data, self.theta)
        delta = predictions - self.labels
        theta = self.theta
        theta -= alpha*(1/num_examples)*(np.dot(delta.T, self.data))
        self.theta = theta
        print(self.theta)
        return theta


    def hypothesis(data, theta):
        predictions = np.dot(data, theta)
        return predictions

    def cost_function(self, data, labels):
        num_examples = data.shape[0]
        delta = LinearRegression.hypothesis(self.data, self.theta) - labels
        cost = (1/2) * np.dot(delta.T, delta)
        return cost[0][0]

    def get_cost(self, data, labels):
        data_processed = data.mean()

        return self.cost_function(data_processed, labels)

    def predict(self, data):

        data_processed = (data - data.mean())/(data.std())
        print(data_processed)
        print(self.theta)
        predictions = LinearRegression.hypothesis(data_processed, self.theta.T)
        return predictions






if __name__ == "__main__":

    train_data = np.array([[1.616, 1.482, 1.480, 1.564, 1.443,
                          1.503, 1.479, 1.405, 1.494, 1.484, 1.375,
                          1.109, 1.487, 1.546, 1.535, 1.487, 1.463,
                          1.741, 1.441, 1.252, 1.626, 1.107, 1.352,
                          1.185, 1.153, 1.692, 1.343, 1.217, 0.872, 1.233],
                         [7.537, 7.521, 6.441, 6.423, 7.468, 7.376,
                          7.315, 7.314, 6.098, 6.086, 6.084, 7.078,
                          7.006, 6.993, 6.375, 6.356, 6.890, 6.862,
                          6.714, 6.651, 6.647, 6.635, 6.609, 6.598,

                          6.578, 6.572, 6.526, 6.453, 6.453, 6.452]])
    train_data = pd.DataFrame(train_data.T, columns = ['Species Biomass', 'Species Density'])
    x_train = train_data['Species Biomass']
    y_train = train_data['Species Density']

    test_data = np.array([[1.430, 1.127, 1.433, 1.384, 1.870, 1.070,
                           1.530, 1.361, 1.632, 1.325, 1.488, 1.291],
                          [7.504, 7.493, 6.421, 6.402, 6.977, 6.951,
                           6.343, 6.168, 6.105, 7.283, 7.283, 7.212]])

    test_data = pd.DataFrame(test_data.T, columns = ['Species Biomass', 'Species Density'])
    x_test = test_data['Species Biomass']
    y_test = test_data['Species Density']



    plt.figure(figsize=(30, 30))
    plt.scatter(x_train, y_train, label='Train Data', s=200)
    plt.scatter(x_test, y_test, label='Test Data', s=200)
    plt.title("Relationship between species biomass and species density"， fontsize='30')
    plt.xlabel("Species Biomass"， fontsize='30')
    plt.ylabel("Species Density"， fontsize='30')
    plt.legend(fontsize=30)
    plt.show()

    num_iterations = 50
    learning_rate = 0.01

    linear_regression = LinearRegression(x_train, y_train)
    (theta, cost_history) = linear_regression.train(learning_rate, num_iterations)


    plt.figure(figsize=(30, 30))
    plt.plot(range(num_iterations), cost_history)
    plt.xlabel('Times'， fontsize='30')
    plt.ylabel('Cost'， fontsize='30')
    plt.show()

    predictions_num = 30
    x_predictions = np.linspace(1, 2, predictions_num).reshape(30, 1)
    y_predictions = linear_regression.predict(x_predictions) + 6.8

    plt.figure(figsize=(30, 30))
    plt.scatter(x_train, y_train, label='Train Data', s=200)
    plt.scatter(x_test, y_test, label='Test Data', s=200)
    plt.plot(x_predictions, y_predictions, 'r')
    plt.title("Relationship between species biomass and species density"， fontsize='30')
    plt.xlabel("Species Biomass"， fontsize='30')
    plt.ylabel("Species Density"， fontsize='30')
    plt.legend(fontsize=30)
    plt.show()

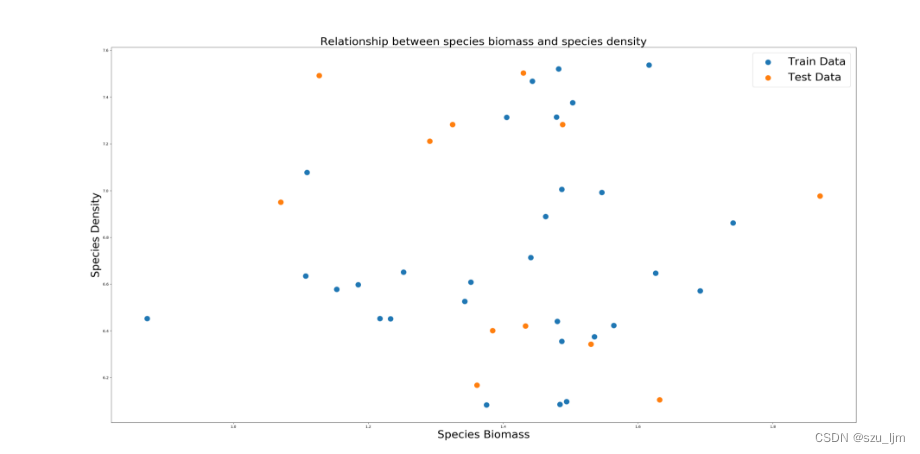
某年某地区生物量和种群密度散点图

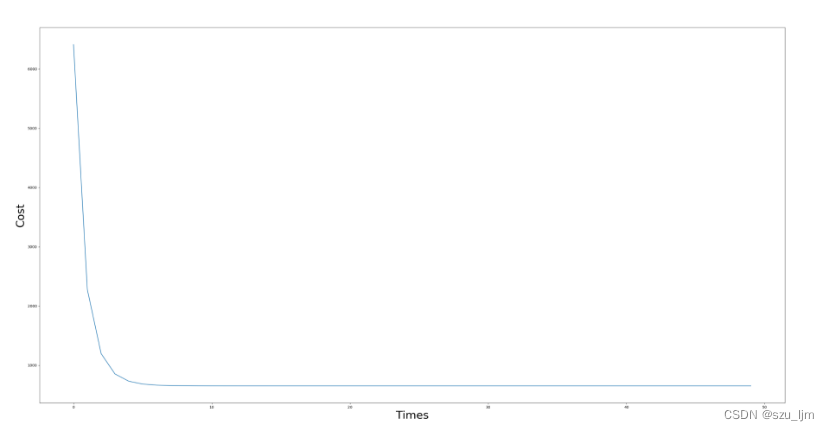
损失值随训练次数的变化

回归方程

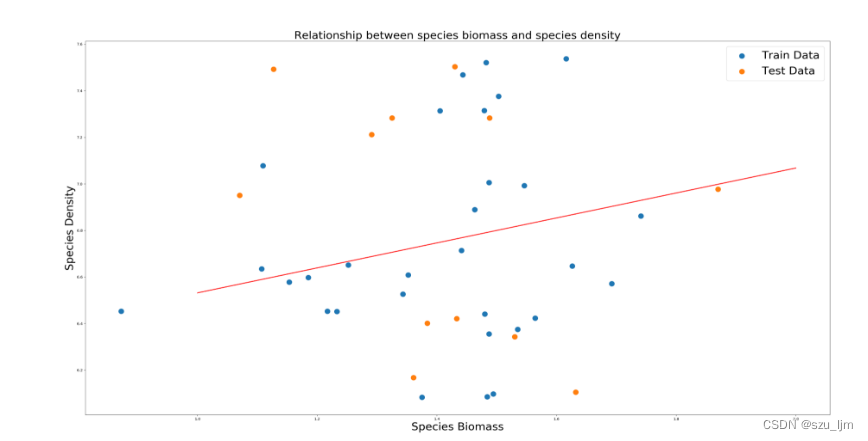
因为上述代码缺少数据预处理模块所以拟合效果不佳，需要加入合适的数据预处理代码

总结

以上就是今天的机器学习之线性回归的笔记内容，机器学习的回归类模型中除了线性回归，还有逻辑回归，岭回归等等，这类模型主要用于预测类问题，模型的好坏要根据模型的精度来评判。

机器学习是博主比较感兴趣的一个领域，博主从高二接触到《终极算法》这本书，书里面介绍了机器学习中具有里程碑意义的几个模型：知识图谱，神经网络和多层感知机，支持向量机，遗传算法等，看完这本书后博主就对机器学习萌发了很大的兴趣，不过机器学习对数学的要求比较高，所以在未来的时间里，希望自己不负热爱，在探索机器学习和其背后的数学原理的道路上上下求索，享受知识带来的神秘和快乐