这是Strang 教授的第一讲,引出线性代数的核心问题:求解线性方程组,在几何空间中直观的理解方程组的解表达的意义,理解在线性代数中求解方程组的核心思想:寻找系数矩阵A列向量的某个或某些线性组合,使得线性组合的结果向量等于b。两个核心的概念:线性方程组的行图像和列图像,其中列图像尤为重要。
举例说明线性方程组航图像和列图像的概念:
e.x. 有2个方程2个未知数的线性方程组:
系数矩阵A,
未知数向量x,
右侧向量b。
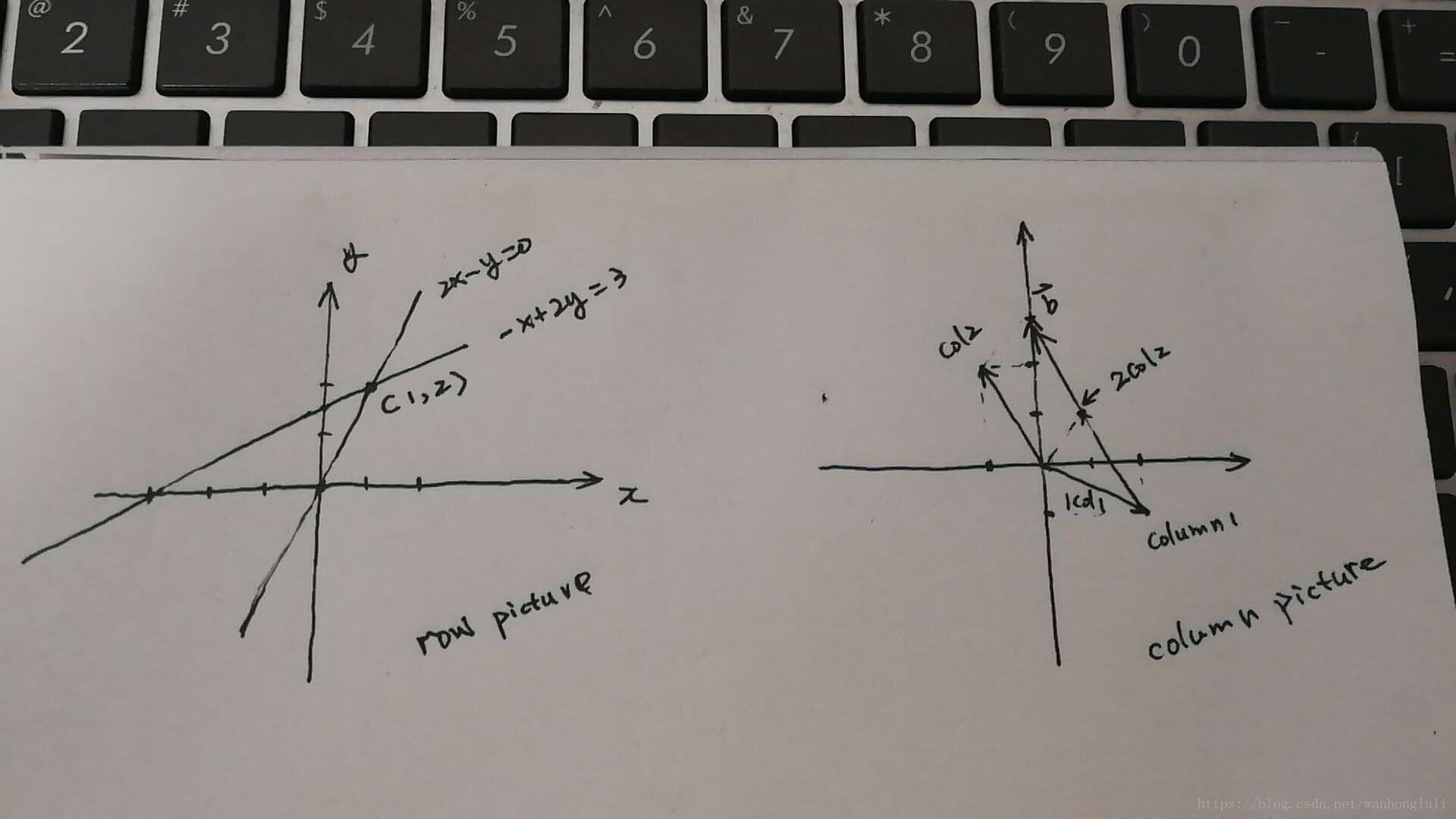
若我们以未知数向量的的两个分量x,y建立坐标系,那么我们将在两个方程作图在xy坐标系下得到两条直线,两条直线的焦点的坐标即为我们方程组的解,这是在中学课本中就学过的作图方式,解的意义也很明确,就是方程组构成直线的交点,推广到3维解在行图像中即是3个平面的交点或交线,因为每个方程构建了一个平面,推广到更高维行图像可能并不直观,因为我们生活在三维空间中,简单可以理解成更加高维的平面相交,例子中的行图像:
我们在向量的基本概念 - 线性代数课时0(MIT Linear Algebra , Gilbert Strang)从书本中摘抄过线性方程组矩阵表示Ax=b的列向量线性组合表达形式:
若我们以系数矩阵A的列向量的两个分量建立坐标系,那么我们在坐标系中将得到(2,-1)、(-1,2)、(0,3)这3个向量,那么我们求解线性方程组的过程就是找到合适的标量x,y使得x(2,-1) + y(-1,2) = (0,3),在坐标系中由系数矩阵列向量和方程组右侧向量构成的就是所说的列图像,在列图像中求解线性方程组的解释变为寻找适合的系数矩阵列向量的线性组合,例子中的列图像:
行图像和列图像诠释了求解线性方程组的两种不同思想:一种是求解未知数坐标系下方程构成的线,平面(高维平面)的交点(线、面),另一种是求解系数矩阵列向量坐标系列向量的适当线性组合(线性代数的核心思想)。
本文最后记录下Strang教授在方程组的几何解释视频最后提到的矩阵乘向量(Ax)的两种计算方式(前面已经用到了):
1. 取A的一列向量x对应行上的标量相乘,将得到的所有列向量相加即得到Ax的结果,看作是A的列向量的线性组合。
2.取A的行向量与向量x做内积得到结果向量对于行位置上的标量,当行向量取完,即也得到了结果向量。
内容对应《INTRODUCTION TO LINEAR ALGEBRA》2.1章节。