【凸优化学习笔记2】仿射集、凸集、凸锥

参考资料：
1.凌青老师的凸优化课（b站）
2.Stephen Boyd的《凸优化》中译本（清华大学出版社）

文章目录

什么是凸优化

先大致看一下凸优化的定义。

对于一个优化问题，如果目标函数和约束函数都是凸函数，即对任意的 $\in\mathbf{R}^{n}$ 和 $\alpha,\beta\in\mathbf{R}$ ，且满足 $\alpha+\beta=1,\alpha\geqslant0,\beta\geqslant0$ ，下列不等式成立：
$f_{i}(\alpha x+\beta y)\leqslant\alpha f_{i}(x)+\beta f_{i}(y)，i=0,1,...,m$
这样的函数即为凸函数。

也就是目标函数是凸函数，约束是一个凸集（即约束也由若干个凸函数组成），这样的问题凸优化问题。

这个定义比较绕。
下面开始从一系列基本概念(如仿射集)，一步步将思路导向凸优化。

仿射集（Affine Set）

空间中两点连成的直线、线段的表达

先讲讲贯穿空间中的两个点 $x_1$ 、 $x_2$ （ $x_1,x_2\in\mathbf{R}^{n}$ ）的直线如何表达：
定义一个变量实数 $\theta\in\mathbf{R}$ ，则有直线：
$y=\theta x_1+(1-\theta)x_2$
一定贯穿 $x_1$ 、 $x_2$ 两点。
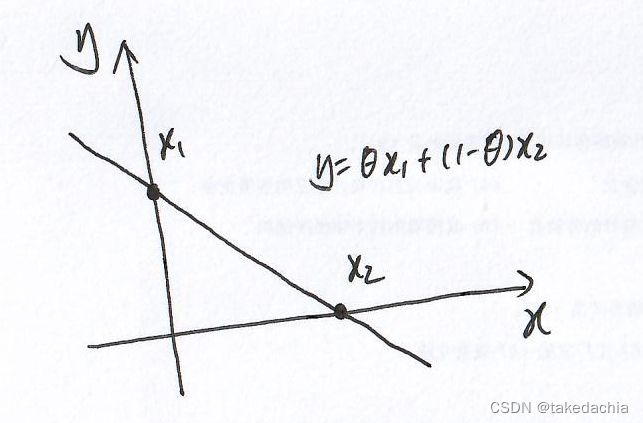
在这里插入图片描述

如果要将这条线上的点集限制在两点之间，需要限定 $\theta$ 的范围在0到1之间。
那么 $y=\theta x_1+(1-\theta)x_2，\theta\in[0,1]$ 则表示为连接两点的线段。

仿射集

先看一个直观的定义：如果一个集合 $C$ 是仿射集，则任意选取集合中两点 $x_1,x_2\in C$ ，则连接 $x_1,x_2$ 的直线也在集合内。

由此可见，一条直线本身也是一个仿射集，而线段不是仿射集(线段上两点的连线是直线)。
整个二维空间 $\mathbf{R}^{2}$ 也是一个仿射集。二维空间中的一个正方形点集就不是仿射集。

我们可以对仿射集做一个更复杂严谨的定义：
设 $x_1,...,x_k\in C，{\theta}_1,...,{\theta}_k\in \mathbf{R}$ ，
且 ${\theta}_1+...+{\theta}_k=1$ ，
我们定义一个仿射组合： $\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}$
如果 $C$ 是一个仿射集，那么这个仿射组合仍然在 $C$ 内。

寻找具有良好性质的仿射集

如上，已知一个（由两点定义的）仿射集：
$C$ 是仿射集， $x_1,x_2\in C$ ，那么 $\theta x_1+(1-\theta)x_2\in C$

我们看这个仿射集， $x_1,x_2$ 的系数要求和为1。
那么可不可以存在一个仿射集，不需要有这样的系数和为1的要求呢？
即：
$C$ 是仿射集， $x_1,x_2\in C$ ，那么 $\alpha x_1+\beta x_2\in C$ ， $\alpha ,\beta$ 为实数。

可以寻找一下这样的仿射集。
①假设有一个二维空间中的直线，它是一个仿射集，过 $x_1,x_2$ 两点。设 $\alpha ,\beta=1$ ，那么 $x_1+x_2$ 这点不在这条线上。这个仿射集不具有这样的性质。
②将这条直线移到过原点，我们会发现， $x_1+x_2$ 在直线上，且无论 $\alpha ,\beta$ 取何值，点都在这条线上。这个仿射集具有这样的性质！
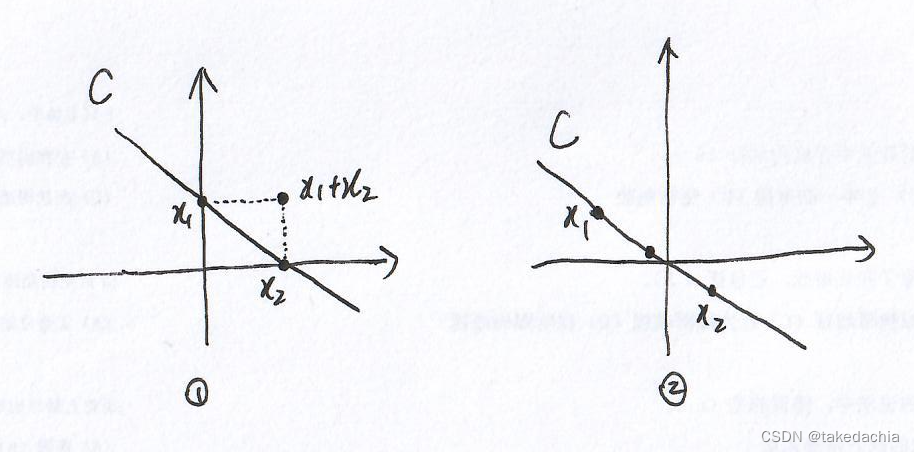
在这里插入图片描述

我们来探究这样的仿射集如何得到。
如果能得到这样的构造方法，我们就可以从一个普通的仿射集中通过一种简单变换，构造出一个特殊的仿射集，使其具有良好的性质（如 $\alpha ,\beta$ 取值不受限）。

任意给一个仿射集 $C$ （注意它不满足 $\alpha x_1+\beta x_2\in C$ ）， $C$ 中所有的元素都减去 $x_0$ ，而 $x_0$ 也是取自 $C$ 中的任意一个元素，这样得到一个新集合 $V$ 。
即 $C$ 相对 $x_0$ 做了一个平移。
那么这个新集合 $V$ 是与 $C$ 相关的一个子空间。
即：
$V=C-x_{0}=\left\{x-x_{0} \mid x \in C\right\}，x_0 \in C$

那么对于这个集合 $V$ ：
①它是一个仿射集
②它具有性质： $x_1,x_2\in V$ ，那么 $\alpha x_1+\beta x_2\in V$ ， $\alpha ,\beta\in\mathbf{R}$ 。
（证明见凌青老师的视频或书）

总结一下：
如果有任意一个仿射集 $C$ ，我们做一个平移变换 $C-x_0$ ，可构造出一个新的仿射集，它是原仿射集的一个子空间。
（注意这个子空间是与 $C$ 相关的子空间，它不能脱离于 $C$ 单独存在）
由于减去了一个自己包含的 $x_0$ ，它必定经过原点。
它具有比较良好的性质，比如 $\alpha x_1+\beta x_2\in C$ ，其中 $\alpha+\beta$ 不再要求等于1。

线性方程组的解是仿射集

任意一个线性方程组的解空间都是一个仿射集。

比如我们有以下线性方程组：
$C=\{x \mid A x=b\}$ ，其中 $\in \mathbf{R}^{m \times n}, b \in\mathbf{R}^{m}, x\in\mathbf{R}^{n}$
集合 $C$ 是该线性方程组的解集(解空间)，可以证明集合 $C$ 是一个仿射集。

证明：
在这里插入图片描述
我们一样可以构造 $C$ 的子空间，我们可以证明 $C$ 的零空间（把b改成0，即 $\{x \mid A x=0\}$ ）就是一个子空间，具有和之前的构造仿射集一样的良好性质。

反过来说，任意一个仿射集，也可以写成一个线性方程组的解集。

仿射包

现在我们考虑这样一个问题：
有任意集合 $C$ （不一定是仿射集），我们如何构造尽可能小的仿射集？

我们称这样的集合为仿射包，记为 $\text {aff } C$ 。
在集合 $C$ 中任意取 $k$ 个点，构造一个仿射组合，把所有这样的仿射组合放到一个新的集合中，即为集合 $C$ 的仿射包。
表示为：
$\text { aff } C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \cdots, x_{k} \in C, \theta_{1}+\cdots+\theta_{k}=1\right\}$

举例：
①如果C是空间中两个点，它的仿射包是一条直线
②如果C是空间中三个点，它的仿射包是整个空间 $\mathbf{R}^{2}$
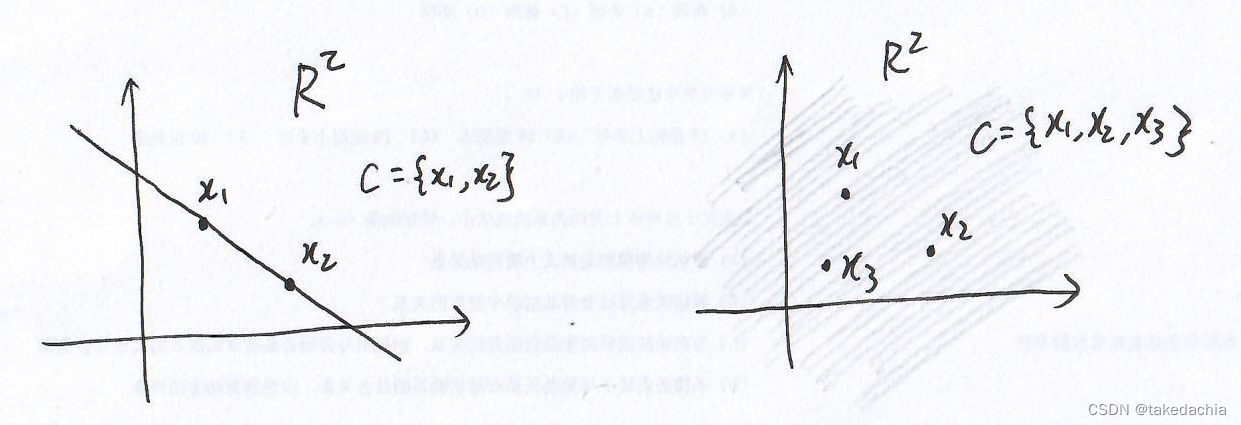
在这里插入图片描述

③如果 $C$ 是一个仿射集，它的仿射包就是它本身。

凸集（Convex Set）

凸集的学习类比仿射集。仿射集是直线，凸集就是线段。

凸集和凸组合

如果一个集合 $C$ 是凸集，它的任意两点之间的线段仍然在 $C$ 内。
即 $x_1,x_2\in C$ ，存在任意 ${\theta}\in [0,1]$ ，使
$\theta x_{1}+(1-\theta) x_{2} \in C$

因此仿射集是凸集的一个扩展情形，凸集要求更严格。

凸组合类比仿射组合的定义。多了[0,1]区间限制。

一个集合 $C$ ，设任意点 $x_1,...,x_k\in C，{\theta}_1,...,{\theta}_k\in \mathbf{R}$ ，
且 ${\theta}_1+...+{\theta}_k=1$ ， ${\theta}_1,...,{\theta}_k\in[0,1]$
那么点 $\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}$ 为（点 $x_1,...,x_k$ 的）一个凸组合。

这样我们可以扩充凸集的定义，即：
如果 $C$ 为凸集，那么 $C$ 中任意元素的凸组合都 $\in C$

凸包(Convex Hull)

我们也可以从任意集合 $C$ ，构造尽可能小的凸集。

我们称这样的集合为凸包，记为 $\text {conv } C$ 。
在集合 $C$ 中任意取 $k$ 个点，构造一个凸组合，把所有这样的凸组合放到一个新的集合中，即为集合 $C$ 的凸包。
表示为：
$\text {conv } C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \cdots, x_{k} \in C,{\theta}_1,...,{\theta}_k\in[0,1], \theta_{1}+\cdots+\theta_{k}=1\right\}$

凸集和凸包的例子

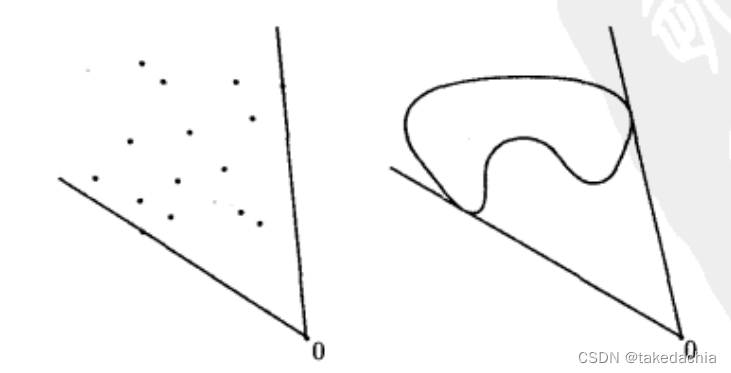
几个二维空间凸集的例子：
在这里插入图片描述
凸包的图例：

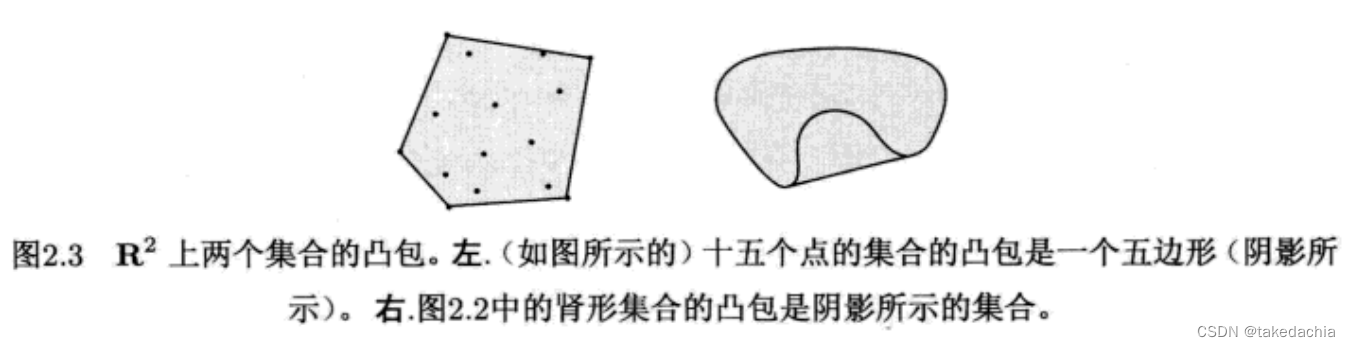
上图的点集的凸包可以理解成用一根橡皮筋绑住外围点的样子。

凸锥（Convex Cone）

锥、凸锥的定义

我们先看看锥和凸锥的定义。

锥（Cone）：
集合 $C$ 是锥，那么对于 $C$ 中任意一个元素 $x$ ，取 $\theta\geqslant0$ ，一定有： $\theta x\in C$

凸锥（Convex Cone）：
集合 $C$ 是凸锥，那么对于 $C$ 中任取至少两个元素 $x_1,x_2$ ，取 ${\theta}_1,{\theta}_2\geqslant0$ ，一定有： ${\theta}_1x_1+{\theta}_2x_2\in C$

上面凸锥的概念中， ${\theta}_1,{\theta}_2$ 必须要非负，但和凸集相比没有和为1的限制。

图例

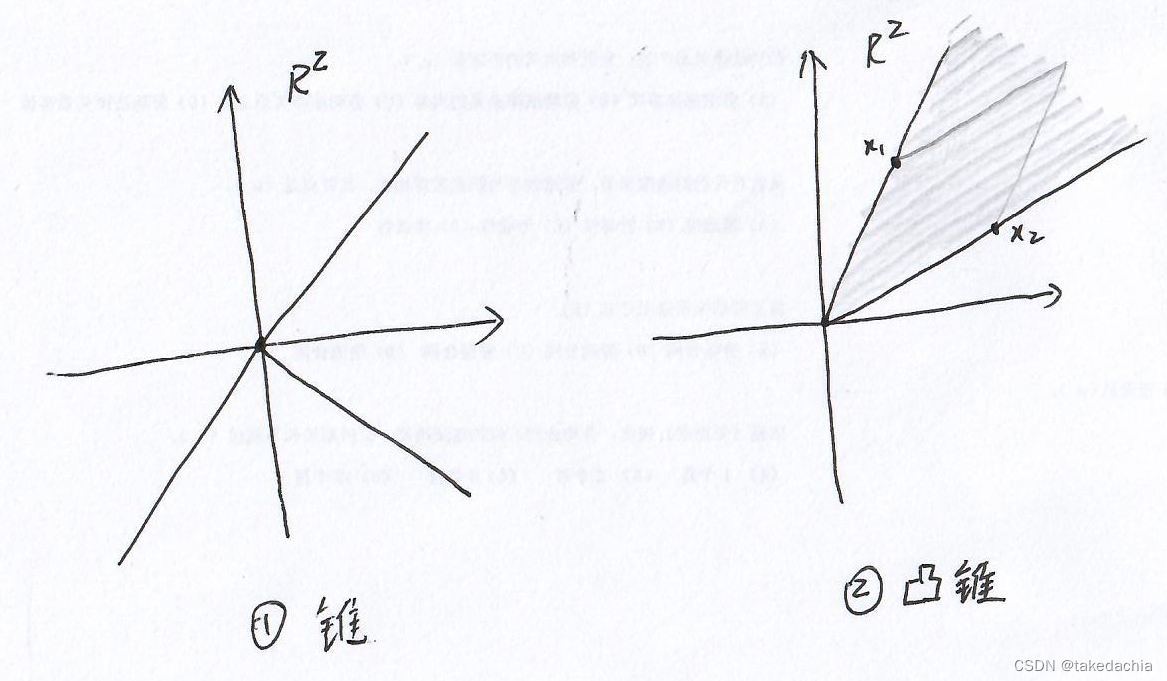
在这里插入图片描述

①二维空间中，有从原点出发的三条射线，所有射线上的点构成一个集合。
这个集合符合锥的定义，所以它是一个锥。
并且我们能想象如果这些射线不是从原点发射出去的，那就不是一个锥。
但这个集合不是一个凸锥。

②二维空间中，有从原点出发，由两条射线围成了一个往外无线延伸的扇形。
我们在其上任取两点 $x_1,x_2$ ，设系数 ${\theta}_1,{\theta}_2$ 为1，那么根据平行四边形法则，其向量和一定也在这个扇形区域内。
这个集合就是一个凸锥。

所以我们看到锥系列的最大特征是过原点。
它是非负齐次的。

凸锥组合、凸锥包

类比仿射组合、凸组合，我们可以定义凸锥组合。以及凸锥包。

凸锥组合：
一个集合中取任意点 $x_1,...,x_k$ ，
且 ${\theta}_1,...,{\theta}_k\geqslant0$
那么点 $\theta_{1} x_{1}+\cdots+\theta_{k} x_{k}$ 为（点 $x_1,...,x_k$ 的）一个凸锥组合。

凸锥包即包含集合本身的最小凸锥。
即取集合中任意点的凸锥组合都在凸锥包内。
$\text {凸锥包 } C=\left\{\theta_{1} x_{1}+\cdots+\theta_{k} x_{k} \mid x_{1}, \cdots, x_{k} \in C,{\theta}_1,...,{\theta}_k\geqslant0\right\}$

凸锥包的图例：
在这里插入图片描述