在优化问题中，寻找最优解过程中两个基本的难点：一是局部最优不一定是全局最优，而通过各类算法找到的最优值往往是局部最优值；其次便是约束条件的复杂性导致求解算法的复杂性大幅度增加。凸优化问题的优势在于其局部最优解就是全局最优解，技巧与难点体现在描述问题的环节，一旦问题被建模为凸优化问题，求解过程相对来说就非常简单。

1 基本概念

1.1 仿射集

若集合 $C\subseteq R^{n}$ 中任意两个不同点的直线仍在集合 $C$ 中，那么集合$C$是仿射的。根据上述定义，可以将 $C\subseteq R^{n}$ 是仿射的等价为：对于任意的 $x_1,x_2 \in C$ 及 $θ∈R$ 有 $θx_1+(1-θ)x_2∈C$。这个概念可以拓展到多个点的情况有：对任意 $x_1,...,x_k∈C$ 并且 $θ_1+⋯+θ_k=1$ 其中 $θ_1,…,θ_k∈R$ ，那么 $θ_1 x_1+,…,+θ_k x_k$ 仍然在 $C$ 中。

1.2 凸集

仿射集中定义的是任意点确定的直线上的点均在仿射集内，凸集中则定义为任意点确定的线段上的点均在凸集内，按照线段的定义，可以将θ的条件更改为\[θ_i≥0，θ_i∈R，i=1,…,k\] \[θ_1+⋯+θ_k=1\]以符合凸集的定义。

1.3 凸函数

1.3.1 凸函数定义与性质

有函数 $f:R^n→R$ ，如果对于任意的 $x,y∈dom\ f$ 且 $dom f $ 也为凸集，并且 $0≤θ≤1$ ，有\[f(θx+(1-θ)y)≤θf(x)+(1-θ)f(y)\]那么函数 $f:R^n→R $ 是凸函数。从几何意义上看，上述式子意味着在点 $(x,f(x))$ 和点 $(y,f(y))$ 之间的线段，在函数 $f$ 的图像上方。

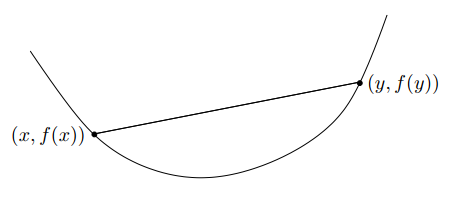
图1-1 凸函数示意图
凸函数的另一个性质：有函数 $f:R^n→R$ ，如果对于任意的 $x∈dom\ f$ 且 $dom\ f$ 也为凸集， $v∈R^n$，若函数 $g(t)=f(x+tv)$为凸函数，其中 $dom\ g = \{t|x+tv∈dom\ f\}$，则函数 $f$为凸函数。这一性质可以理解为：若函数是凸的，则当且仅当其在与其定义域相交的任何直线上都是凸的。
上述的两点凸函数性质中，第一个性质较为实用，第二个性质更适合于理论分析。

1.3.2 凸函数一阶条件与二阶条件

凸函数的一阶及二阶条件也经常被用来判定函数是否为凸函数。对于一阶条件来说，若函数 $f:R^n→R$ 是凸函数，则有式\[f(y)≥f(x)+∇f(x)^T (y-x)\]成立。其中函数$f$可微，$x,y∈dom\ f$ 且 $dom\ f$ 也为凸集。上述条件为充要条件。
对于二阶条件，设函数 $f:R^n→R$二阶可微，则\[f为凸函数⇔∀x∈dom f,∇^2 f(x)≽0\]其中$x∈dom \f$ 且 $dom\ f$ 也为凸集。

1.4 拟凸函数

对于函数$f:R^n→R$，若其定义域及所有下水平集（α-sublevel set）
\[S_α = \{x∈dom\ f | f(x)≤α\}\]α∈R，都是凸集，则函数f为拟凸函数。由定义可以得出，下水平集其实是函数f定义域的某个区间，同时也可以得出凸函数是拟凸函数的一种特殊情况。

2 保凸运算

在凸优化的实际运用或理论推导计算过程中，有时可以将简单的凸函数构造成新的、复杂的凸函数，使其更加适合解决问题。这种构造新的凸函数过程就叫做保凸运算，其核心就是构造后的函数还能保证其凸性。

2.1 非负加权和

若函数 $f_i (i=1,…,m)$为凸函数，则\[f= w_1 f_1+⋯+w_m f_m\]依然是凸函数。

2.2 复合仿射映射

有函数 $f:R^n→R$，并且$A∈R^{m×n}$，$b∈R^n$，定义函数$g:R^m→R$为
\[g(x)=f(Ax+b)\]其中$ dom g={x | Ax+b∈dom f }$。则有：若$f$为凸函数，则$g$也为凸函数。

2.3 复合函数

给定函数$h:R^k→R$和$g:R^n→R^k$，定义复合函数$f=h°g:R^n→R$为
\[f(x)=h(g(x)),dom\ f=\{x∈dom g\ |\ g(x)∈dom\ h\}\]则函数f的保凸与保凹满足的结论如下，其中函数$g$和$h$二次可微并且定义域均为$R$。
若$h$为凸且非减，$g$为凸，则f为凸函数。
若$h$为凸且非增，$g$为凹，则f为凸函数。
若$h$为凹且非减，$g$为凹，则f为凹函数。
若$h$为凸且非增，$g$为凸，则f为凹函数。

3 凸优化问题

优化问题的一般形式如下式所示。
\[minimize\ f_0 (x)\]\[subject\ to\ f_i (x)≤0，i=1,…,m\]\[h_i (x)=0，i=1,…,p\]称x∈R^n为优化变量，$f_0:R^n→R$为目标函数，$f_i (x)≤0$为不等式约束，对应的$f_i (x)$为不等式约束函数，$h_i (x)≤0$为等式约束，对应的$h_i (x)$为等式约束函数。对于目标函数和约束函数来说，其有定义的点的集合的交集即为优化问题的定义域，表达式如式\[D=⋂_{i=0}^m\ dom\ f_i \ ∩\ ⋂_{i=1}^p\ dom\ h_i\]
所有可行点的集合称为可行集或约束集。定义x^为优化问题的最优解，另外p^为优化问题的最优解的集合，此时P^*定义为\[p^*\ =\ inf⁡\{f_0 (x) \ |\ f_0 (x)≤0,i=1,…,m, h_i (x)=0,i=1,…,p\}.\]
在求解优化问题时，有时候并不需要得出精确的最优解，仅需接近最优解即可，因此满足$f_0 (x)≤p^*+ϵ，ϵ>0$的可行解称为$ϵ-$次优解，$ϵ-$次优解的集合称为$ϵ-$次优集。
对于凸优化而言，相较于一般标准形式的优化问题，凸优化问题要求$f_0 (x)$为凸函数，$f_i (x)$也为凸函数，$h_i (x)$为仿射函数，其余相关概念与一般优化问题并无不同。因此凸优化问题的形式如下所示。
\[minimize\ f_0 (x)\]\[subject\ to\ f_i (x)≤0，i=1,…,m\] \[h_i (x)=a_i^T x+b_i=0，i=1,…,p\]

4 拉格朗日对偶

4.1 Lagrangian函数

Lagrangian函数的基本思想是在目标函数中考虑一般优化问题的约束条件，即添加约束条件的加权和，得到增广的目标函数。定义Lagrangian函数$L:R^n×R^m×R^p→R$为\[L(x,λ,ν)=f_0 (x)+∑_{i=1}^mλ_i f_i(x)+∑_{i=1}^pν_i h_i(x),\]
L函数的定义域为$dom\ L=D×R^m×R^p$，$D$集合定义由第3节已经给出。$λ_i 、ν_i$称为拉格朗日乘子。

4.2 Lagrange对偶函数

有了Lagrangian函数后，可以定义Lagrange对偶函数$g:R^m ×R^p→R$为\[g(λ,ν)= inf_{x∈D}L(x,λ,ν)=inf_{x∈D}⁡\left(f_0 (x)+∑_{i=1}^mλ_i f_i(x)+∑_{i=1}^pν_i h_i(x)\right) ,\]
其中$λ∈R^m，ν∈R^p$，根据函数定义来看，其为Lagrange对偶函数关于$x$取最小值。因为对偶函数是一组关于$(λ,ν)$的仿射函数的逐点下确界，所以即使如第3节中所述的标准形式优化问题并不是凸优化问题，其Lagrange对偶函数也是凹的，这一点值得关注。

4.3 对偶问题

对于任意一组$(λ,ν)$，其中$λ≽0$，根据Lagrangian对偶函数的定义，其函数值为原优化问题的最优值$p^*$的一个下界。对于求出最大的下界，使其最为接近$p^*$这个问题可以表述为优化问题
\[maximize \ g(λ,ν)\]\[subject\ to \ λ≽0\]该优化问题就称为对偶问题，设$d^*$为对偶问题的最优值，同样的$λ^* 、ν^*$称为最优拉格朗日乘子。$(p^*-d^*)$称为对偶间隙，当$p^*=d^*$时称为强对偶性，对应的$p^*≥d^*$称为弱对偶性，因为$d^*$一定是$p^*$的某个下界，因此不存在$p^*<d^*$的情况。对于一般情况下的优化问题来说强对偶性并不成立，但是当优化问题是凸优化问题时，强对偶性通常（但不总是）成立。

5 KKT条件

对于目标函数和约束函数可微的任意优化问题，如果其强对偶性成立，那么任何一对原问题最优解和对偶问题最优解必须满足KKT条件。KKT条件共有5条，如下所示：
\[f_i (x^* )≤0,\ i=1,…,m\]\[h_i (x^* )=0, \ i=1,…,p\]\[λ_i^*≥0, \ i=1,…,m\]\[λ_i^* f_i (x^* )=0, \ i=1,…,m\]\[∇f_0 (x^* )+∑_{i=1}^mλ_i^* ∇f_i (x^* )+∑_{i=1}^pν_i^* ∇h_i (x^* )=0\]
上述KKT条件中，第一条和第二条是原问题的可行性，第三条是对偶问题的可行性，第四条是互补松弛条件，第五条是稳定性条件。
对于非凸问题来说KKT条件仅仅是必要条件，而对于优化问题为凸问题来说KKT条件为充要条件。也因此对凸优化问题的算法设计基本均是围绕KKT条件来进行的。

6 算法设计

本节中所涉及的无论是有约束还是无约束优化问题全为凸优化问题。
对于优化问题来说，任何的算法都是迭代的算法。在每个迭代算法中的每一次迭代均会有\[x^(k+1)=x^k+α^k d^k\]的计算。$x^k$表示第k时刻已经算出来的解。$α^k$表示步长，其为一维标量。$d^k$表示k时刻的方向，与$x$的维数相同。迭代算法主要是围绕$α^k$和$d^k$的更新展开的。

6.1 下降方法

使用下降方法时，需要确保下降方向$d^k$已经确定。因此下降方法主要解决如何确定下降步长$α^k$的问题。

6.1.1 Amijo Rule法

Amijo Rule法是一种模糊的步长算法，也称Back tracking方法。在该迭代算法中，若\[ f_0 (x^k+α^k d^k )>f_0 (x^k )+γα(∇f_0 (x^k ))^T d^k，\]则迭代继续，否则停止。在该式中，每次迭代都由 $α=αβ$ 来更新 $α$ 的值。其中一般来说$γ∈(0,0.5)，β∈(0,1)$。$γ$ 表示可以接受的f的减少量占基于线性外推预测的减少量的比值，正常取值在0.01到0.3之间。参数 $β$ 的正常取值在0.1到0.8之间，$β$ 取值越小搜索越粗糙。在计算时通常 $α$ 的初始值会比较大，一般从1开始迭代。

6.1.2 黄金分割法

黄金分割法如图所示。

比较A、B两点的函数值，若A大则将 $α_min$更新为A点横坐标，若B大则将 $α_max$更新为B点横坐标。如此重复迭代找出最优值。

6.2 无约束优化算法

根据第5节提出的KKT条件，对于无约束优化问题来说，KKT条件就被简化成了\[∇f_0 (x^* )=0\]这一仅存的条件。因此求解无约束优化问题等价于求解 $n$ 个变量的 $n$ 个方程的线性方程组，特殊情况下可以通过直接求解上述KKT条件来获得最优解，但是一般情况下必须采用迭代算法求解该KKT条件。

6.2.1 梯度下降法

梯度下降法即使用梯度的负方向作为搜索方向，即$d^(k+1)=-∇f(x^k)$。其步长$α^{k+1}$由6.1节中的介绍的下降方法或其他计算方法计算出来。下降方法的使用前提是需要首先知道下降方向，因此梯度下降算法的第一步是计算下降方向，第二步为通过下降方法计算步长，最终更新$x^{k+1}$的值。
梯度下降法的停止准则通常为$‖∇f(x)‖_2≤ε$，其中 $ε$ 是一个极小的正数。大部分情况下确定下降方向后就判断迭代是否需要停止，而不是确定步长后判断。

6.2.2 最速下降法

对$f(x+v)$在$x$出进行一阶泰勒展开有\[f(x+v)≈f ̂(x+v)=f(x)+(∇f(x))^T v，\]运用在最速下降时，将式中的 $x$ 换成 $x^k$ 就有\[f(x^k+v)≈f ̂(x^k+v)=f(x^k )+(∇f(x^k ))^T v，\]下降方向$d^(k+1)$由式\[d^{k+1}=arg⁡min_v⁡\{f(x^k )+(∇f(x^k )^T )v \ |\ ‖v‖=1\}\]
可得。对于$v$来说，可以选择不同的范式来进行约束，同时得到的结果也不尽相同。当$‖v‖$为1范数时，则其方向为负梯度的沿坐标轴最大分量方向。当$‖v‖$为2范数时其与梯度下降法算出的下降方向类似，仅仅只是对其做了正则化。与梯度下降法类似，最速下降法也是首先找到最速下降方向，然后计算步长，最后更新$x^{k+1}$，直到满足停止准则迭代停止。

6.2.3 坐标轮换法

很多时候计算梯度是比较麻烦的一件事，因此为了简便，直接沿不同坐标方向轮换地进行搜索。轮换过程中每次允许一个变量变化，其余变量保持不变，在搜索的过程中可以不需要目标函数的导数，只需目标函数值信息。
设$x∈R^n$，则$d^k=e_{mod(k,n)}$，其中e表示单位向量，表示第$mod(k,n)$个元素为1。利用坐标轮换法计算出来的搜索方向不一定是下降方向，因此步长应该按搜索方向确定步长，即$-α_{max}≤α^k≤α_{max}$。

6.2.4 牛顿法/拟牛顿法

牛顿法中 $d^k=-(∇^2 f(x^k ))^{-1} ∇f(x^k )$ 为最优 $d^k$，即牛顿方向为当前点的Hessian矩阵的逆乘以负梯度的方向。对于牛顿法来说有以下算法流程：\[ (1)\ \ \ \ Repeat\ d^k=-(∇^2 f(x^k ))^{-1} ∇f(x^k )\]\[ α^k=arg min\{f(x^k+αd^k )\},0≤α≤α_{max}\]\[ x^{k+1}=x^k+α^k d^k\]\[(2)\ \ \ \ Until\ convergence\ or \left|(∇f(x^k ))^T (∇^2 f(x^k ))^{-1} ∇f(x^k )\right|≤ε\]
牛顿法的优势在于其收敛速度较梯度下降法、最速下降法快，对坐标选择或者目标函数的下水平集不敏感，当问题规模比较大时与规模较小的问题性能相似，并不依赖于算法参数的选择。但是牛顿法的最大缺点在于Hessian矩阵的计算与存储成本较高，因此诞生了拟牛顿法。例如在拟牛顿法中的BFGS算法核心思想便是找到一个合适的矩阵 $B$ 来代替Hessian矩阵，以此简化Hessian矩阵，实现更好的数值稳定性。

6.3 等式约束优化算法

仅具有等式约束的优化问题的KKT条件可以简化为\[h_i (x^* )=0, i=1,…,p ，\]\[∇f_0 (x^* )+∑_{i=1}^pν_i^* ∇h_i (x^* )=0\]两条。同时等式约束优化问题形式如\[minimize\ f_0 (x)\]\[subject\ to\ Ax=b\]

6.3.1 牛顿法

等式约束优化问题中的KKT条件若是非线性的，则将其进行泰勒二阶展开使其线性化，因此牛顿法主要用来解决非线性的KKT条件问题。根据KKT条件的二阶泰勒展开与等式约束的凸优化问题形式，其方向 $d^k$ 可由式\[ \begin{vmatrix}{∇^2 f(x^k)} & {A^T} \\ A& 0\\ \end{vmatrix} \begin{vmatrix}{d^k}\\ 0\\ \end{vmatrix} = \begin{vmatrix}{-∇^2 f(x^k)} \\ 0\\ \end{vmatrix}\]得。步长依然使用6.1节中介绍的方法或其他方法计算得出。

6.3.2 拉格朗日法

含等式约束的优化问题，且KKT条件非线性，也可以使用拉格朗日法来进行求解，但是拉格朗日法多用于理论分析研究，在实际运用中使用较少。拉格朗日法的求解如下所示：\[ \left \{ \begin{array}{l} x^{k+1}=x^k-α^k (∇f{x^k }+A^T v^k) \\ v^{k+1}=v^k+α^k (Ax^k-b) \end{array} \right. \]

6.3.3 增广拉格朗日法

增广拉格朗日法对等式约束优化问题更为有效。增广拉格朗日函数形式如\[L_c (x,v)=f(x)+v^T (Ax-b)+c/2 ‖Ax-b‖_2^2\]
所示。其中 $c>0$，$c$ 可以是常量也可以是变量。
增广拉格朗日函数有两个性质：
1.若$v=v^*$，则对$∀c>0$来说均有\[x^*=arg min_x⁡L_c (x,v^*)\]
2.若$c→∞$，则对于$∀c$来说均有\[x^*=arg min_x⁡L_c (x,v)\]
根据上述，可得增广拉格朗日算法如下：
\[x^{k+1}=arg min_x⁡L_c (x,v^k)⇔x^{k+1}=\frac{(c-v^k)}{(c+1)}\]
\[v^{k+1}=v^k+c(Ax^{k+1}-b)\]

6.3.4 交替方向法

假设有无约束优化问题min f(x)+g(x)，将其转化为等式约束优化问题\[minimize\ \ \ \ f(x)+g(z)\]
\[subject\ to\ \ \ x=z\]
那么其增广拉格朗日函数就可以写成
\[L_c (x,z,v)=f(x)+g(z)+v^T (x-z)+\frac c2 ‖x-z‖_2^2.\]
依据6.3.3小节的拉格朗日法，有优化步骤：
\[(1)\ \ \ \ \{x^{k+1},z^{k+1} \}=arg min_{x,z}⁡\left\{f(x)+g(z)+(v^k)^T (x-z)+\frac c2 ‖x-z‖_2^2 \right\}\]
\[(2)\ \ \ \ v^{k+1}=v^k+c(x^{k+1}-z^{k+1})\]
将第一步分解为2步进行迭代
\[(1.a)\ \ \ \ x^{k+1\ |\ t+1}=arg min_x⁡\left\{f(x)+\frac c2 ‖x-z^{k+1\ |\ t}+\frac {v^k}c‖_2^2 \right\}\]
\[(1.b)\ \ \ \ z^{k+1\ |\ t+1}=arg min_z⁡ \left\{f(x)+\frac c2 ‖z-x^{k+1\ |\ t}-\frac {v^k}c‖_2^2 \right\}\]
在优化步骤1中，若是用代码来表示，则会有两重循环，将其分解为两个一重循环的方法即1.a和1.b称为交替方向的拉格朗日乘子法。交替方向的拉格朗日乘子法在图像处理、分布式计算中较为常用。

7 总结

凸优化问题的求解均围绕着KKT条件来进行，各式各样的算法均有其适用的场合，并不存在优劣之说。当一个问题确定为凸优化问题后，往往比较容易被解决，最难的还是在于对实际问题进行数学建模，建立好有效的优化模型后，实际上问题就已经解决百分之八十。数学建模过程中，如何有效地根据实际问题、预估最优解来合理抛弃部分约束使问题简单化才是优化问题的难点。

8 参考文献

Boyd,Stephen,and Lieven Vandenberghe.Convex optimization.Cambridge university press,2004.

凸优化学习笔记