仿射，仿射集，凸集

学习凸优化的过程中，首先要接触到仿射集与凸集的定义，非常有必要完全理解。

关于锥、凸锥参看另一篇博文：https://blog.csdn.net/robert_chen1988/article/details/78828727

一、仿射集（Affine set），凸集（Convex set）定义

设 $x_1$ 与 $x_2$ 是定义在集合 $C$ 中任意两个不同的点，即 $x_1\neq x_2$ , 并且 $x_1, x_2\in C, C\subseteq \bf{R}^n$ ，对任意一个实数 $\theta$ ，都有

θ x_{1} + (1 - θ) x_{2} \in C o r x_{2} + θ (x_{1} - x_{2}) \in C

$\theta x_1+(1-\theta)x_2\in C\quad or\quad x_2+\theta(x_1-x_2)\in C$
则称

C

$C$ 为一个仿射集。 若要求 $0\leq\theta\leq 1$ ，则 $C$ 为一个凸集，可见 一个仿射集必属于凸集（锥跟仿射集并没有隶属关系）。

仿射集的几何意义是：一个集合中任意两点的连线上的点仍然属于这个集合，则该集合为仿射集。个人感觉在三维空间内，整个坐标系才属于仿射集。

注：每一个线性方程组 $Ax=b$ 的解为一个仿射集。

为什么称作仿射呢？定义 $y=\theta x_1+(1-\theta) x_2$ ，该表达式可以化为

y = x_{2} + θ (x_{1} - x_{2})

$y=x_2+\theta(x_1-x_2)$

y

$y$ 可以表示为通过基点

x_{2}

$x_2$ ，方向为

x_{1} - x_{2}

$x_1-x_2$ ，大小为

θ (x_{1} - x_{2})

$\theta(x_1-x_2)$ 的一个箭头的末端，如下图所示：

import matplotlib.pyplot as plt
import numpy as np

plt.arrow(2, 3, 4, 8, width = 0.08, color = 'c', length_includes_head = True)

plt.plot(2, 3, 'ro')
plt.annotate('$x_2$', xy = (2.2, 2.8))
plt.plot(5, 9, 'ro')
plt.annotate('$x_1$', xy = (5.2, 8.8))
plt.plot(6, 11, 'ro')
plt.annotate('$y=x_2+\\theta (x_1-x_2), \\theta = 2$', xy = (6.2, 10.8))
plt.xlim((0, 10))
plt.ylim((0, 16))
plt.show()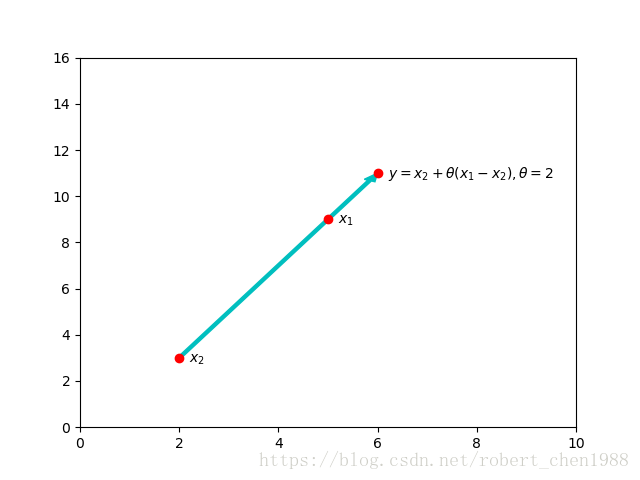

这里写图片描述
若 $C$ 是一个仿射集， $x_1$ , $\dots$ , $x_k\in C$ ，并且 $\theta_1+\dots+\theta_k=1$ ，则

θ_{1} x_{1} + \dots + θ_{k} x_{k} \in C

$\theta_1x_1+\dots+\theta_k x_k\in C$
其中，

θ_{1} x_{1} + \dots + θ_{k} x_{k}

$\theta_1x_1+\dots+\theta_k x_k$ 称作点

x_{1}, \dots, x_{k}

$x_1, \dots, x_k$ 的 仿射组合。
若要求

θ_{i} \geq 0, i = 1, \dots, k

$\theta_i\geq 0, i = 1, \dots, k$ ，则

θ_{1} x_{1} + \dots + θ_{k} x_{k}

$\theta_1x_1+\dots+\theta_k x_k$ 称作点

x_{1}, \dots, x_{k}

$x_1, \dots, x_k$ 的 凸组合。

二、子空间(Subspace)

对于一个仿射集 $C$ ，及其内部任意一点 $x_0$ ，集合

V = C - x_{0} = {x - x_{0} ∣ x \in C}

$V=C-x_0=\{x-x_0\mid x\in C\}$
称作一个子空间。 仿射空间可以看做对一个子空间的平移。

性质1：一个子空间 $V$ 为仿射集。
性质2：一个子空间 $V$ 为凸锥。
性质3：一个子空间 $V$ 为凸集。

证明：对于 $V$ 中任意两点 $v_1$ 与 $v_2$ ，它们的线性组合 $\alpha v_1+\beta v_2$ ，因为

α v_{1} + β v_{2} + x_{0} = α (v_{1} + x_{0}) + β (v_{2} + x_{0}) + (1 - α - β) x_{0} \in C

$\alpha v_1+\beta v_2 + x_0= \alpha(v_1+x_0)+\beta(v_2+x_0)+(1-\alpha-\beta)x_0\in C$
(因为

v_{1} + x_{0} \in C

$v_1+x_0\in C$ ,

v_{2} + x_{0} \in C

$v_2+x_0\in C$ , 仿射集定义)
所以

α v_{1} + β v_{2} \in V

$\alpha v_1+\beta v_2 \in V$ ，即一个子空间中任意两点的线性组合仍然属于该子空间。
特别的，我们令

α = 1 - β

$\alpha=1-\beta$ ，则根据仿射集定义，子空间属于一个仿射集。
特别的，我们令

α > 0, β > 0

$\alpha>0,\beta>0$ ，则根据凸锥的定义，子空间属于一个凸锥。
若我们令

α = 1 - β, 0 \leq α \leq 1

$\alpha=1-\beta, 0\leq\alpha\leq 1$ ，则估计凸集定义，子空间属于一个凸集。
综合以上，子空间也属于凸锥。

◻

$\Box$

一条直线是一个仿射集合，一个通过原点的直线属于子空间（证明过程类似上面）

三、仿射包（affine hull）

一个集合 $C$ 内所有点的仿射组合，称作该集合的仿射包，即 aff $C$ :

aff C = {θ_{1} x_{1} + \dots + θ_{k} x_{k} ∣ x 1, \dots, x_{k} \in C, θ_{1} + \dots + θ_{k} = 1}

$\text{aff}~ C=\{\theta_1x_1+\dots+\theta_kx_k\mid x1,\dots, x_k\in C, \theta_1+\dots+\theta_k=1\}$