1.最优化问题概述
最优化问题是决策问题,选择一些可以执行的策略使得目标最优;一个最优化问题包括
- 决策变量;
- 一个或多个目标函数;
- 一个由可行策略组成的集合,可由等式或者不等式刻画;
最优化问题的形式:

最优化问题的分类
- 无约束优化问题和约束优化问题
- 线性规划和非线性规划:目标函数与约束条件均为优化变量的线性函数即为线性优化,有一个为非线性函数即为非线性优化
- 连续优化和离散优化:可行集是连续的还是离散的
- 单目标优化和多目标优化:即目标函数是单个还是多个,我们在机器学习中通常引入权重将多目标优化转化为单目标优化
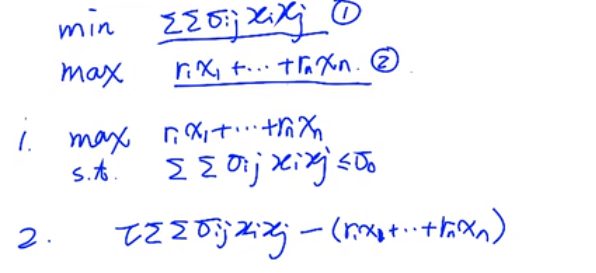
- 随机优化和确定性优化:即约束函数的参数是否确定。对于随机优化问题,处理方法有如下几种(1)针对不同参数下取均值,用均值代替约束函数(2)概率约束,即要求找到一组可行集使得各种参数下满足约束函数的概率大于某个值。(3)鲁棒优化,即在参数范围内要求最坏的参数的情况满足约束函数。

2.凸集
引论
凸函数与非凸函数
对于凸函数而言(左图),任意平稳点即为全局最优解,对于非凸优化问题(右图)而言,平稳点可能是全局最优点,还有可能是局部最优点
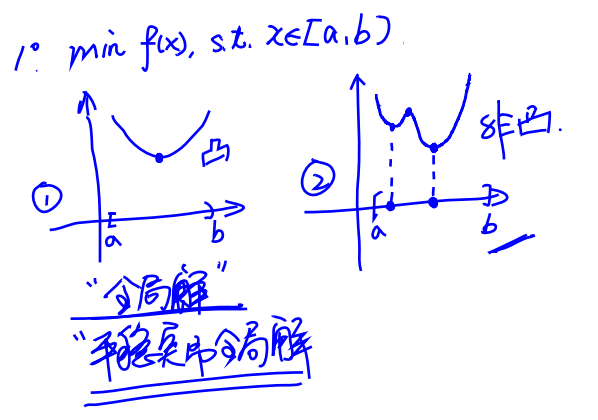
凸集和非凸集
对于凸集,满足最优解X*负梯度方向和与所有(x-x*)夹角大于等于90度,而对于非凸集,不一定满足X*负梯度方向和与所有(x-x*)夹角大于等于90度

凸集

即:集合中两点的连线仍属于此集合.
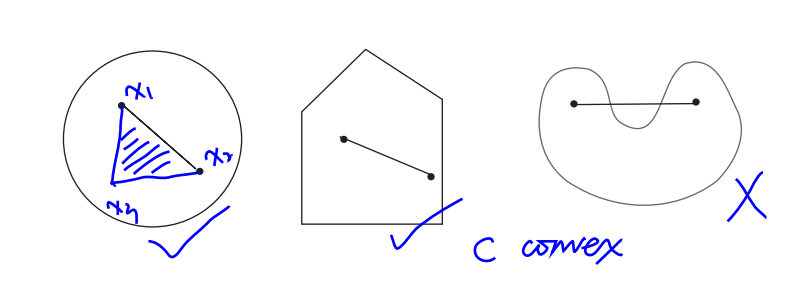
我们可以拓展到集合中的三个点,集合中三个点可形成一个面,也是属于该集合。
凸集的等价定义为:
凸组合:我们称点x=为点x1,...,xk的凸组合,其中,
凸包:集合C中所有点的凸组合组成的集合称为C的凸包conv C
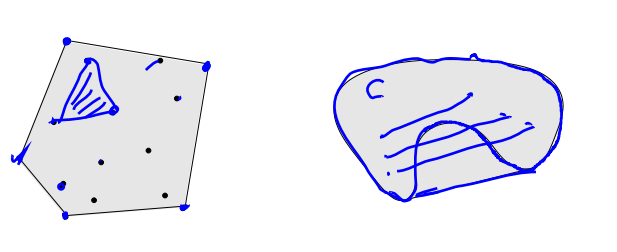
凸包不仅仅包含凸集,也包含非凸集,集合的凸包是包含该集合的最小凸集,如下图所示,对于凸集来说,其凸包为其本身,而对于非凸集来说,凸包能够将其转化为凸集。
常见的凸集:

多面体:多个线性不等式所刻画的集合


尤其需要说明的是下面的半定矩阵锥,首先是什么是半正定矩阵,什么是正定矩阵?设n元实二次型,如果对于任意
,都有f(x)>0,则称f为正定二次型,并称实对称矩阵A为正定矩阵。它的A的特征值全为正,各阶顺序主子式均大于0.而半正定就是加个等号。
第一个问题: 所有的半正定矩阵组成的集合是锥吗?
对于正定矩阵A的特征值,
对应的特征值
,故能够证明
也是正定的,即
。半正定与之类似。
既然半正定矩阵组成的集合是锥,那么由锥的性质,它也是凸的。

保凸运算

仿射变换:仿射变换是一种线性变换,如果集合是凸的,仿射变换后也是凸的

证明过程:

投影定理及证明过程

直观理解:
投影定理的意思相当于,我们从以y为圆心的一个集合和集合C的交集找一个点,使其到y的距离最小,因为这个交集(凸集)是有界的,所以这个最小的点一定存在

对于唯一性:假设存在两个点,使其到y的距离最小,那么我们可以找到这两个点连线的中点,使其到y的距离更小,由此得出了矛盾。

对于投影定理的充要条件,它的含义是集合C中的点和投影点的连线形成的向量与投影点和y点形成的向量夹角为钝角。

支撑超平面定理
补充说明:集合的闭包就是包含集合边界的一个集合,当集合为闭集时,闭包就是它本身,为开集时,它包含了集合的边界。因此,凸集的闭包依然是凸集。


Farkas引理

这个问题的集合解释是A的行向量与c向量的关系,
- 第一个问题说的是,我们能不能找到一个向量,这个向量与所有的a向量夹角大于等于90度,但是与c向量的夹角小于90度,很显然,我们通过作图可以看出,当且仅当c向量位于a向量外部的时候成立
- 第二个问题说的是,我们能不能找到一个正的线性组合,使得所有的a向量能够表示c向量,我们能够通过作图看出,当且仅当c向量位于a向量内部的时候成立

证明过程:
