文章目录
【1】逻辑回归
在这部分的练习中,你将建立一个逻辑回归模型来预测一个学生是否能进入大学。假设你是一所大学的行政管理人员,你想根据两门考试的结果,来决定每个申请人是否被录取。你有以前申请人的历史数据,可以将其用作逻辑回归训练集。对于每一个训练样本,你有申请人两次测评的分数以及录取的结果。为了完成这个预测任务,我们准备构建一个可以基于两次测试评分来评估录取可能性的分类模型。
1.Visualizing the data
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
path = 'ex2data1.txt'
data = pd.read_csv(path,header=None,names=['Exam 1','Exam 2','Admitted'])
data.head()#查看前5行数据
| Exam 1 | Exam 2 | Admitted | |
|---|---|---|---|
| 0 | 34.623660 | 78.024693 | 0 |
| 1 | 30.286711 | 43.894998 | 0 |
| 2 | 35.847409 | 72.902198 | 0 |
| 3 | 60.182599 | 86.308552 | 1 |
| 4 | 79.032736 | 75.344376 | 1 |
data.describe()

创建散点图使数据更加直观地展示出来
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(x = positive['Exam 1'],y = positive['Exam 2'],s = 50,color='b',marker = 'o',label = 'Admitted')
ax.scatter(x = negative['Exam 1'],y = negative['Exam 2'],s = 50,color='r',marker = 'x',label = 'Not Admitted')
plt.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()
Admitted = 1表示被录取,用positive将Admitted = 1时的exam1、exam2成绩取出;同理用negative将Admitted = 0时的exam1、exam2成绩取出
画出横轴为exam1纵轴为exam2的散点图,查看Admitted的分布情况
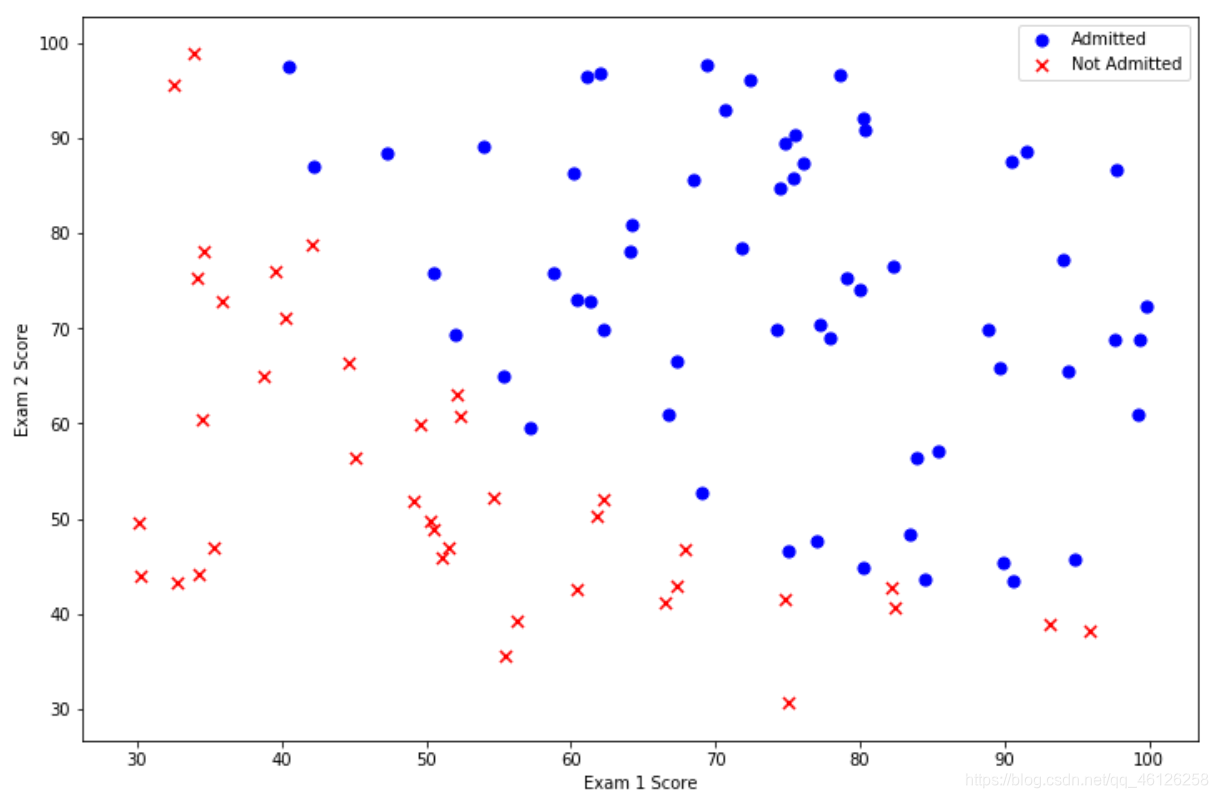
看起来在两类间,有一个清晰的决策边界。现在我们需要实现逻辑回归,那样就可以训练一个模型来预测结果。
获取我们的训练集数据:
def get_X(df):
ones = pd.DataFrame({
'ones':np.ones(len(df))})
data = pd.concat([ones,df],axis=1)
return np.array(data.iloc[:,:-1])#返回ndarray
def get_y(df):
return np.array(data.iloc[:,-1])
def normalize_feature(df):
return df.apply(lambda column:(column-column.mean())/column.std()) #特征缩放
X = get_X(data)
print(X.shape)
y = get_y(data)
print(y.shape)
2.Sigmoid fuction

def sigmoid(z):
return 1 /(1 + np.exp(-z))
让我们做一个快速的检查,来确保它可以工作
fig,ax=plt.subplots(figsize=(8,6))
ax.plot(np.arange(-10,10,step=0.01),sigmoid(np.arange(-10,10,step=0.01)),c='r')
ax.set_ylim((-0.1,1.1))
ax.set_xlabel('z')
ax.set_ylabel('g(z)')
ax.set_title('sigmoid fuction')
plt.plot()
效果如下:(符合S曲线,函数定义正确)

3.Cost fuction
与线性回归的代价函数不同,因为要使用sigmoid函数控制h(x)在(0,1)之间
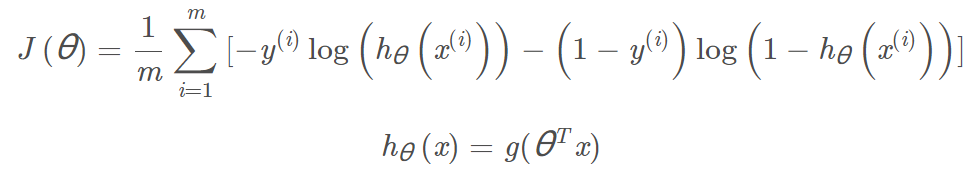
代价函数的推导以及手算过程:

theta=np.zeros(3)
theta #array([0., 0., 0.])
def cost(theta,X,y):
return np.mean(-y *np.log(sigmoid(X@theta)) - (1-y)*np.log(1-sigmoid(X@theta)))
cost(theta,X,y)
#0.6931471805599453
相乘两位置为array时(*)号 为对应元素的乘积,@连接的两项表示对应位置相乘后相加 -> 具体请戳这里
其他矩阵相乘的用法及扩展 -> 请戳这里
4.Gradient
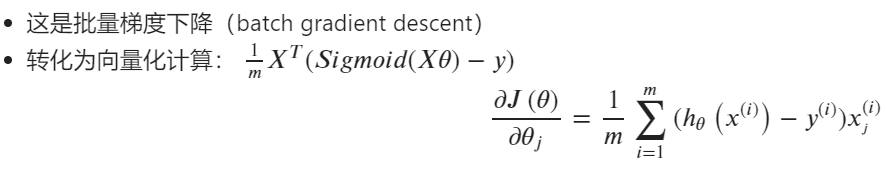
def gradient(theta,X,y):
return ( X.T @ (sigmoid(X @ theta) - y)) / len(X)
分析: X.T @ (sigmoid(X @ theta) - y)此处我认为是活用了@乘积的操作,X.T为(100×3)维,y为一维数列。为了使达到公式中的效果,需要将X进行转置后才能相乘。
注意,在上这一步中我们实际上没有在这个函数中执行梯度下降,我们仅仅在计算一个梯度步长。(只从[0,0,0]开始进行了一次梯度下降,还没有得到最优的θ)现在可以看看用我们的数据和初始参数为0的梯度下降法的结果
gradient(theta,X,y)
#array([ -0.1 , -12.00921659, -11.26284221])
5.Learning θ parameters
我们可以用SciPy的“optimize”命名空间:SciPy’s truncated newton(TNC)实现寻找最优参数。
只需传入cost函数,已经所求的变量theta,和梯度,func = cost表示传入我们的cost函数,x0=theta,表示传入初始点即theta的初值
import scipy.optimize as opt
res = opt.minimize(fun=cost, x0=theta, args=(X,y), method='Newton-CG',jac=gradient)
res
fun: 0.20349770249067073
jac: array([-1.29015205e-05, -7.87933956e-04, -9.06046726e-04])
message: 'Optimization terminated successfully.'
nfev: 72
nhev: 0
nit: 28
njev: 243
status: 0
success: True
x: array([-25.15887187, 0.20621202, 0.20145168])
此时的x=[-25.15887187, 0.20621202, 0.20145168]即为theta的最优解
6.Evaluating logistic regression
接下来,我们需要编写一个函数,用我们所学的参数theta来为数据集X输出预测。然后,我们可以使用这个函数来给我们的分类器的训练精度打分。
def predict(theta, X):
probability = sigmoid( X @ theta)
return [1 if x >= 0.5 else 0 for x in probability] # return a list
final_theta = res.x
y_pridict = predict(final_theta, X)
用skearn中的方法来检验
from sklearn.metrics import classification_report
print(classification_report( y,y_pridict))
'''
precision recall f1-score support
0 0.85 0.87 0.86 39
1 0.92 0.90 0.91 61
accuracy 0.89 100
macro avg 0.88 0.89 0.88 100
weighted avg 0.89 0.89 0.89 100
'''
我们的逻辑回归分类器预测正确,如果一个学生被录取或没有录取,达到89%的精确度

f1-score 即 F
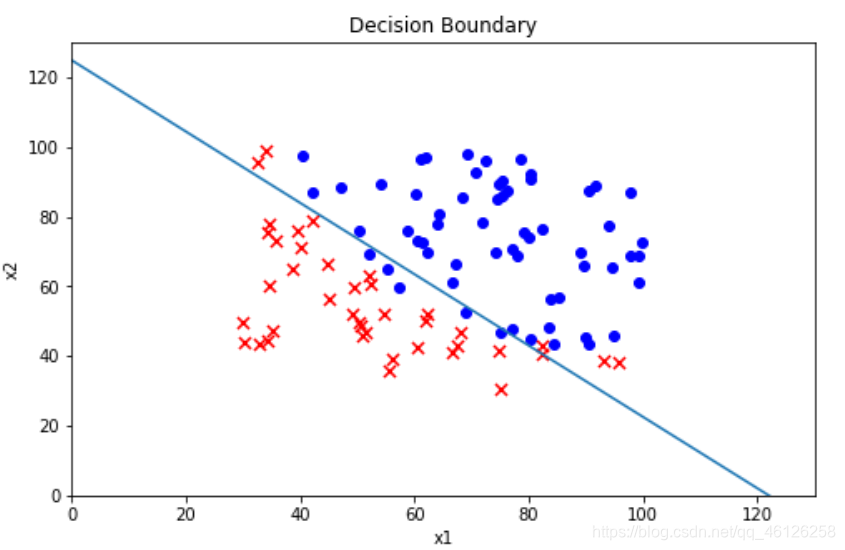
7.Decision boundary
更直观地展示出所拟合的参数是否被录取的效果,所以需要根据参数画出决策边界(线性函数)
公式:
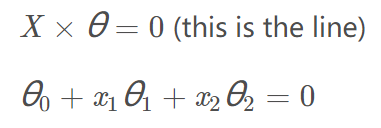
函数推导:

斜率矩阵:
coef = -(res.x / res.x[2])
coef
#array([124.88787185, -1.02363018, -1. ])
函数实现:
x = np.arange(130, step=0.1)
y = coef[0] + coef[1]*x
data.describe()

根据原始数据画散点图,根据函数画决策边界
fig, ax = plt.subplots(figsize=(8,5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], c='b', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x, y)
ax.set_xlim(0, 130)
ax.set_ylim(0, 130)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Decision Boundary')
plt.show()
效果如下: