【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（6）：生成树算法

Offer 驾到，掘友接招！我正在参与2022春招打卡活动，点击查看活动详情。”

@TOC

前言

Hello！小伙伴！ 非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～   自我介绍 ଘ(੭ˊᵕˋ)੭ 昵称：海轰 标签：程序猿｜C++选手｜学生 简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python 学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！   机器学习小白阶段 文章仅作为自己的学习笔记 用于知识体系建立以及复习 知其然 知其所以然！

系列文章

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（1）：图的基本概念

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（2）：图的矩阵表示

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（3）：路径与连通

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（4）：有向图的连通性

【机器学习｜数学基础】Mathematics for Machine Learning系列之图论（5）：树及其性质

2.5 生成树算法

2.5.1 构造生成树的方法

求连通图的生成树的两种方法：

• 破圈法
• 避圈法

破圈法

1. 从连通图 $G$开始，若 $G$中含有圈，则去掉圈上的一边
2. 若 $G$中还有圈，再去掉圈上的一条边
3. 重复上面步骤，直至 $G$中不含圈为止
4. 最后得到的便是 $G$的不含圈的连通生成子图，即生成树

避圈法

1. 在 $G$中任选一条边 $e_1$
2. 然后找一条不与 $e_1$形成圈的边 $e_2$，得到 $\{e_1,e_2\}$
3. 再找一条不与 $\{e_1,e_2\}$形成圈的 $e_3$，得到 $\{e_1,e_2,e_3\}$
4. ...
5. 当找不到一条边不与 $\{e_1,e_2,e_3,...,e_i\}$形成圈，则 $G[\{e_1,e_2,e_3,...,e_i\}]$是 $G$的生成树

2.5.2 最小生成树算法

定义2.12

（1）图 $G$的每条边赋予一个实数 $w(e)$，称为 $e$的权

此时图 $G$称为加权图

（2）设 $G_1$是 $G$的生成子图，则 $G_1$的权定义为

$w(G_1)=\sum_{e\in E(G_1)}w(e)$

最小生成树

一个图的权最小的生成树称为最小生成树

权最大的生成树则称为最大生成树

Kruskal算法

$T_0$：存放生成树的边的集合，初态为 $\phi$ $C(T_0)$：最小生成树的权，初值为零 $VS$：部分树的顶点集的集合，其初值为： $\{\{v_1\},\{v_2\},...,\{v_n\}\}$ 输入边的端点数组 $A(\varepsilon),B(\varepsilon)$及边权数组 $w(\varepsilon)$

算法步骤：

1. $T_0\leftarrow\phi,\quad C(T_0)\leftarrow0,\quad VS\leftarrow\{\{v_1\},\{v_2\},...,\{v_n\}\}$，将 $E$中的边按权从小到大排成队列 $Q$
2. 若 $|VS|=1$，输出 $T_0,C(T_0)$，停止。 否则转下一步
3. 从 $Q$中取出排头边 $(u,v)$,并从 $Q$中删除 $(u,v)$
4. 若 $u,v$在 $V,S$的同一元素 $V_1$中，则转3，否则分属两个集合 $V_1,V_2$,进行下一步
5. $T_0\leftarrow T_0 \cup\{(u,v)\},\quad V \leftarrow V_1 \cup V_2,\quad VS \leftarrow VS-\{V_1\}-\{V_2\}+V,\quad C(T_0)\leftarrow C(T_0)+C(u,v)$，转2

步骤4 中 $u,v$在 $V,S$的同一元素 $V_1$中，说明若添加 $u,v$这条边会形成圈，不符合生成树条件，所以不添加，继续进行下一步

---

用 $Kruskal$算法求下图的最小生成树

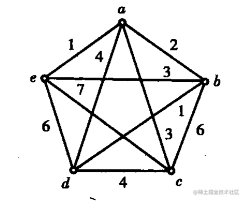
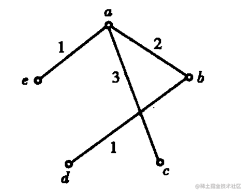
总结

• 先对图中所有边按照权进行排序，从小到大
• 从权小的边开始选，依次递增
• 只要选择的这条边加入之前已经选好后的图中不形成圈，则可以添加该边，否则不添加

定理2.10

Kruskal算法选得的边的导出子图是最小生成树

Prim算法

$L(v)$： $v$到子树 $T_0$的直接距离 输入加权连通图的带权邻接矩阵 $C=(C_{ij})_{n×n}$

算法步骤：

1. $T_0\leftarrow \phi, \quad C(T_0)\leftarrow0, \quad V^{'}=\{v_0\}$
2. 对每一点 $v \in V - V{'}, \quad L(v) \leftarrow C(v, v_0)$（若 $(v,v_0)\notin E,则C(v,v_0)=\infty$）
3. 若 $V^{'}= V$，输出 $\quad T_0,C(T_0)$，停机。否则转下一步
4. 在 $V - V^{'}$中找一点 $u$，使得 $L(u)=min\{L(v)｜v\in (V - V^{'})\}$，并记住 $V^{'}$中与 $u$相邻的点为 $w,e=(w,u)$
5. $T_0\leftarrow T_0\cup\{e\},\quad C(T_0)\leftarrow C(T_0)+C(e), \quad V^{'}\leftarrow V^{'}\cup \{u\}$
6. 对所有 $v\in V - V^{'}$，若 $C(v,u) < L(u)$，则 $L(v)\leftarrow C(v,u)$，否则 $L(v)$不变
7. 转3

---

用 $Prim$算法求下图的最小生成树

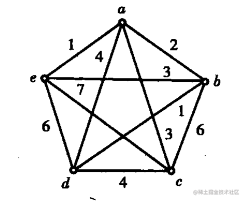
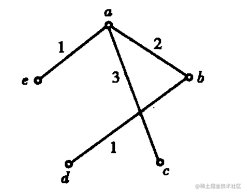
总结

• 任意在图中选一个点，构成子树 $T_0$
• 然后找距离 $T_0$中所有顶点最近的一个顶点（边权最小）
• 找到符合最近的顶点然后加入 $T_0$
• 重复第二步
• 终止条件就是所有的顶点都添加至子树 $T_0$中
• 特别注意：每一步是找距离 $T_0$中所有顶点边权最小的一个顶点

定理2.11

Prim算法产生的图 $G(T_0)$是最小生成树

结语

说明：

• 参考于 课本《图论》
• 配合书中概念讲解 结合了自己的一些理解及思考

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正