详细的介绍请参考这篇博客:SVD奇异值分解
SVD奇异值分解是用来对矩阵进行分解,并不是专门用来求解特征值和特征向量。
而求解特征值和求解特征向量,可以选择使用SVD算法进行矩阵分解后,再用矩阵分解后的结果得到特征值和特征向量。
PCA降维会需要求解协方差矩阵的特征值和特征向量,求协方差矩阵 1 m ∗ X ∗ X T \color{blue}\frac{1}{m}*X*X^T m1∗X∗XT的特征值和特征向量,又可以等价于SVD的其中一种求解矩阵A的三个分解矩阵的方法;
该方法即,利用 A ∗ A T \color{blue}A*A^T A∗AT和 A T ∗ A \color{blue}A^T*A AT∗A来求解A的三个分解矩阵.
所以求出了A的三个分解矩阵,就可以从A的分解矩阵中,间接得到矩阵A*矩阵A转置的特征值和特征向量(这是因为A的三个分解矩阵是和 A ∗ A T \color{blue}A*A^T A∗AT的特征值、特征向量是有关系的),同时也是协方差矩阵 1 m ∗ X ∗ X T \color{blue}\frac{1}{m}*X*X^T m1∗X∗XT的特征值和特征向量。
上面的博客中介绍的SVD奇异值分解的方法中,并没有用到协方差矩阵,不要误解为 A T ∗ A \color{blue}A^T*A AT∗A就是协方差矩阵,因为他们并没有减去均值的操作。并且该SVD的实现算法有很多种,可以不用先求出矩阵 A T ∗ A \color{blue}A^T*A AT∗A ,也能求出我们的右奇异矩阵V。
SVD奇异值分解是使用特殊方法来求解出矩阵的左奇异矩阵U和右奇异矩阵V。但是求解U、V的方法有很多种,并非只有使用 A T ∗ A \color{blue}A^T*A AT∗A这一个方法,而且计算矩阵 A T ∗ A \color{blue}A^T*A AT∗A这个方法计算量太大,不合适。该博客是以这种方法为例,所以这一点需要明白。
需要注意的是,是在PCA降维中才使用了协方差矩阵: X T ∗ X \color{blue}X^T*X XT∗X ,每个维度都做了减去均值的操作后,得到的协方差矩阵就变为了SVD奇异值分解中用到的那种矩阵转置*矩阵的形式,请参考博客深入理解PCA与SVD的关系的第三节。这样,求解的问题就变得一样了
所以,PCA算法可以不用做特征分解,而是做SVD来完成。这个方法在样本量很大的时候很有效。
实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是我们我们认为的暴力特征分解。
PCA降维的方法有下面几种:
(1)直接对样本数据组成的矩阵Xn*n进行求解特征值和特征向量:
这种方式可能是初学者最直接就想到的,他是一种暴力求解方式,当样本特征维度很大时,求解耗时,还可能是复数解。并且,该方法有个硬伤,必须是方阵,即 n ∗ n \color{blue}n*n n∗n的矩阵才能求解特征值和特征向量。
(2)计算协方差矩阵,通过变换矩阵转换来降低维度:
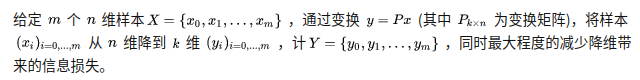
对样本矩阵 X n ∗ m \color{blue}X_{n*m} Xn∗m进行下面操作:
- 求
X的各个维度 均值; - 将
X的各个维度减去该维度均值,再赋值给X,即in place就地操作; - 计算
X的协方差矩阵 C = 1 m ∗ X ∗ X T \color{blue}C=\frac{1}{m}*X*X^T C=m1∗X∗XT; - 对协方差矩阵
C特征值分解; - 从大到小排列
C的特征值; - 取前
K个特征值对应的特征向量按行组成矩阵即为变换矩阵 P k ∗ n \color{blue}P_{k*n} Pk∗n; - Y = P ∗ X \color{blue}Y=P*X Y=P∗X,得到的
Y就是降维后的数据。
该方法会因为:
- (1) 特征维度很大而使得协方差矩阵 C = 1 m ∗ X ∗ X T \color{blue}C=\frac{1}{m}*X*X^T C=m1∗X∗XT
计算量很大; - (2) 计算出了
协方差矩阵后,对协方差矩阵的特征分解的计算效率并不高;
所以也不合适。
(3)将PCA问题转化为SVD问题求解:
SVD奇异值分解是使用特殊方法来求解出矩阵的左奇异矩阵U和右奇异矩阵V。但是求解U、V的方法有很多种,并非只有使用 A T ∗ A \color{blue}A^T*A AT∗A这一个方法,而且计算矩阵 A T ∗ A \color{blue}A^T*A AT∗A 这个方法计算量太大,不合适。该博客是以这种方法为例,所以这一点需要明白。
SVD的实现算法有很多种,可以不用先求出矩阵 X ∗ X T \color{blue}X*X^T X∗XT,也能求出我们的右奇异矩阵V。也就是说,我们的PCA算法可以不用做特征分解,而是做SVD来完成。这个方法在样本量很大的时候很有效。
实际上,scikit-learn的PCA算法的背后真正的实现就是用的SVD,而不是我们我们认为的暴力特征分解。
所以,在第二种方法的基础上,我们求协方差矩阵的计算量很大,就把计算协方差矩阵转化为SVD问题求解,令:

就有:

所以:
- 求 X \color{blue}X X的协方差矩阵 C = 1 m ∗ X ∗ X T \color{blue}C=\frac{1}{m}*X*X^T C=m1∗X∗XT 的特征分解,等价于求 A T ∗ A \color{blue}A^T*A AT∗A的特征分解;
- 又因为, A T ∗ A \color{blue}A^T*A AT∗A的特征分解可以不用求出 A T ∗ A \color{blue}A^T*A AT∗A,而是利用SVD的其他迭代方法得到 A \color{blue}A A的SVD分解
左奇异矩阵U \color{blue}U U、右奇异矩阵V \color{blue}V V和奇异值矩阵 Λ \color{blue}\Lambda Λ; - 通过
右奇异矩阵V \color{blue}V V 和奇异值矩阵 Λ \color{blue}\Lambda Λ(对角阵),得到 A T ∗ A \color{blue}A^T*A AT∗A的特征值和特征向量。即每个特征值对应一个奇异值的平方,每个特征向量对应右奇异矩阵V \color{blue}V V的每列向量; - 求出了特征值和特征向量,取前 k \color{blue}k k 个,就能够求出第二种方法里面的变换矩阵 P k ∗ n \color{blue}P_{k*n} Pk∗n,然后再计算 Y = P ∗ X \color{blue}Y=P*X Y=P∗X,得到的 Y \color{blue}Y Y就是降维后的数据。
PCA的性质:
可参考:【机器学习】降维——PCA(非常详细)
