奇异值分解SVD 与 主成分分析PCA
Reference:
1. 相关知识
1.1 线性代数的线性变换
首先了解一下线性代数的线性变换。
假设有一批数据:
D = [ x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 ] D=\left[\begin{array}{llll}x_1 & x_2 & x_3 & x_4 \\ y_1 & y_2 & y_3 & y_4\end{array}\right] D=[x1y1x2y2x3y3x4y4]那么 S S S 是一个 2 × 2 2\times 2 2×2 的矩阵,如 [ 2 0 0 1 ] \left[\begin{array}{llll}2 & 0 \\ 0 &1 \end{array}\right] [2001],这个矩阵只在对角线上有数字的话,将 D D D 左乘一个 S S S,这个时候实现的就是数据的拉伸操作。
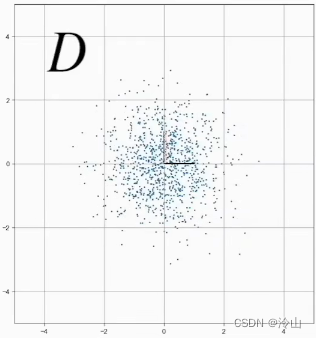

没有拉伸之前,我们有一组基,也就是下图的 i i i 和 j j j,那么 D D D 中的每一组坐标点,可以说是 x k x_k xk 乘以 i i i 加上 y k y_k yk 乘以 j j j,那么左乘 S S S 的时候,相当于是把 i i i 从 [ 1 0 ] \left[\begin{array}{llll}1 \\ 0 \end{array}\right] [10] 变成了 [ 2 0 ] \left[\begin{array}{llll}2 \\ 0 \end{array}\right] [20]。
 这时等于所有数据的点也做相应的拉伸,它代表的就是一个线性变换:
这时等于所有数据的点也做相应的拉伸,它代表的就是一个线性变换:
S D = [ 2 0 0 1 ] [ x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 ] = [ 2 x 1 2 x 2 2 x 3 2 x 4 y 1 y 2 y 3 y 4 ] S D=\left[\begin{array}{ll} 2 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{llll} x_1 & x_2 & x_3 & x_4 \\ y_1 & y_2 & y_3 & y_4 \end{array}\right]=\left[\begin{array}{cccc} 2 x_1 & 2 x_2 & 2 x_3 & 2 x_4 \\ y_1 & y_2 & y_3 & y_4 \end{array}\right] SD=[2001][x1y1x2y2x3y3x4y4]=[2x1y12x2y22x3y32x4y4]另一种线性变换比如说旋转,还是与先前一样, R R R 是一个线性变换矩阵,即 [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] \left[\begin{array}{llll}\cos (\theta) & -\sin (\theta) \\ \sin (\theta) &\cos (\theta) \end{array}\right] [cos(θ)sin(θ)−sin(θ)cos(θ)]。
 将 D D D 左乘一个 R R R,即 R D = [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] [ x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 ] RD=\left[\begin{array}{llll}\cos (\theta) & -\sin (\theta) \\ \sin (\theta) &\cos (\theta) \end{array}\right]\left[\begin{array}{llll}x_1 & x_2 & x_3 & x_4 \\ y_1 & y_2 & y_3 & y_4\end{array}\right] RD=[cos(θ)sin(θ)−sin(θ)cos(θ)][x1y1x2y2x3y3x4y4],得到的结果就是整个数据旋转一个 θ \theta θ。
将 D D D 左乘一个 R R R,即 R D = [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] [ x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 ] RD=\left[\begin{array}{llll}\cos (\theta) & -\sin (\theta) \\ \sin (\theta) &\cos (\theta) \end{array}\right]\left[\begin{array}{llll}x_1 & x_2 & x_3 & x_4 \\ y_1 & y_2 & y_3 & y_4\end{array}\right] RD=[cos(θ)sin(θ)−sin(θ)cos(θ)][x1y1x2y2x3y3x4y4],得到的结果就是整个数据旋转一个 θ \theta θ。


2. 特征值和特征向量
特征值与特征向量的定义如下:
A x = λ x A\mathbf{x}=\lambda \mathbf{x} Ax=λx其中 A A A 是一个 n × n n\times n n×n 矩阵, λ \lambda λ 是矩阵 A A A 的特征值,则 x \mathbf{x} x 是特征值 λ \lambda λ 所对应的 n n n 维特征向量。
将矩阵 A A A 进行特征分解,就可以求出矩阵 A A A 的 n n n 个特征值 λ 1 ≤ λ 2 ≤ … ≤ λ n \lambda_1 \leq \lambda_2 \leq \ldots \leq \lambda_n λ1≤λ2≤…≤λn,以及这 n n n 个特征值所对应的特征向量 w 1 , w 2 , . . . , w n w_1, w_2, ...,w_n w1,w2,...,wn,那么矩阵 A A A 就可以用下式的特征分解表示:
A = W Σ W − 1 A=W\Sigma W^{-1} A=WΣW−1其中 W W W 是这 n n n 个向量合并而成的 n × n n\times n n×n 矩阵,而 Σ \Sigma Σ 为这 n n n 个特征值合并而成的 n × n n\times n n×n 矩阵。一般我们会把 W W W 这 n n n 个特征向量标准化,即满足 ∥ w i ∥ 2 = 1 \|w_i\|_2=1 ∥wi∥2=1,或 w i T w i = 1 w_i^Tw_i=1 wiTwi=1。此时 W W W 的 n n n 个特征向量为标准正交基,满足 W T W = I W^TW=I WTW=I,即 W T = W − 1 W^T=W^{-1} WT=W−1,也就是说 W W W 为酉矩阵1。
说的有点抽象,我们拿个具体的例子来讲:

需要注意的是,要进行特征分解,矩阵 A A A 必须为方阵。
如果 A A A 不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以的,这时就引出了SVD。
3. 奇异值分解
奇异值分解可以写成这种形式:
M = U Σ V T M=U\Sigma V^T M=UΣVT其中 M M M 是我们的原始矩阵,这个矩阵它可以是任意的,不需要是一个方阵,这个矩阵它可以分解成三个矩阵的相乘,即 M = U Σ V T M=U\Sigma V^T M=UΣVT,如下图所示:

[ x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4 ] = [ − − − − − − − − − − − − − − − − ] [ a 0 0 b 0 0 0 0 ] [ − − − − ] \left[\begin{array}{ll}x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_4 & y_4\end{array}\right]=\left[\begin{array}{llll}- & - & - & - \\ - & - & - & - \\ - & - & - & - \\ - & - & - & -\end{array}\right]\left[\begin{array}{ll}a & 0 \\ 0 & b \\ 0 & 0 \\ 0 & 0\end{array}\right]\left[\begin{array}{ll}- & - \\ - & -\end{array}\right] x1x2x3x4y1y2y3y4 = −−−−−−−−−−−−−−−− a0000b00 [−−−−]
U U U 和 V V V 是两个方阵, Σ \Sigma Σ 是一个不规则的矩阵,其对角线上面 a a a 和 b b b 就是奇异值,其他地方都是 0 0 0,也就是说奇异值分解是把原始矩阵分解成上面这三个矩阵的相乘。
如果我们假设奇异值分解在 M M M 为 2 × 2 2\times 2 2×2 矩阵上,此时的 M M M 实际上代表了一个线性变换,但是它的线性变换不是像第一节中讲的旋转或拉伸,这时候 SVD 分解就是把线性变换 M M M 分解为旋转加拉伸再加旋转。如果它是一个正交矩阵的话,那它代表的意义就是一个旋转( U , V U, V U,V),如果它是一个对角矩阵,它代表的意义就是一个拉伸( Σ \Sigma Σ)。


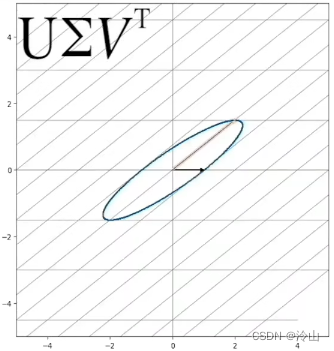
这时 M M M 和 U Σ V T U\Sigma V^T UΣVT 得到的结果是一样的。那么 SVD 分解它到底代表了一个什么样的物理意义呢?
已知 M M M 是一个线性变换,所以在空间上的所有向量,都会被这个线性变换改变它的位置。那如果我们能够找到一组基(在空间上代表正交的一组单位向量),在进行线性变换以后,下左图进行线性变换后,变成了中间的红色,但是它的角度和长度都被改变了;黑色的也是转变到了中图的黑色。

在进行线性变换以后,可以发现这两条还是垂直的。那么如果能找到这样的一组基,线性变换以后它还是垂直的,这个就是 SVD 奇异值分解要找的东西。

如果原来的基第一个方向为 v 1 \mathbf{v_1} v1,第二个方向为 v 2 \mathbf{v_2} v2;那么它转换以后,方向 v 2 \mathbf{v_2} v2 转换到了方向 u 2 \mathbf{u_2} u2,但是它的长度也发生了改变,改变的长度是 σ 2 \sigma_2 σ2, σ 2 \sigma_2 σ2 为奇异值;方向 v 1 \mathbf{v_1} v1 同理。中图两个红色的圆为画的以圆点为中心、两个奇异值为半径做的圆。
然后,再让 V \mathbf{V} V 等于 v 1 \mathbf{v_1} v1、 v 2 \mathbf{v_2} v2 两个向量构成的一个矩阵, U \mathbf{U} U 等于 u 1 \mathbf{u_1} u1、 u 2 \mathbf{u_2} u2 两个向量构成的一个矩阵, Σ \Sigma Σ 是一个奇异值构成的对角阵。
SVD 可以推广到任意大小的矩阵,例如原始矩阵它的大小为 m × n m\times n m×n,分解的 U U U 矩阵是 m × m m\times m m×m, Σ \Sigma Σ 矩阵是一个对角阵,它的大小和原始矩阵的大小是一样的,而 V V V 是 n × n n\times n n×n。

这是最原始的形式,但也是可以改写的:在 M = U Σ V T M=U\Sigma V^T M=UΣVT 形式下,图中示例中间的 Σ \Sigma Σ 矩阵的最后一行全都是 0 0 0,相当于这一行根本就没有信息,那么其实可以把它缩减的,因为 U U U 中最后一列,是乘以的 Σ \Sigma Σ 的最后一行,是没有东西的,所以 U U U 的最后一列就没有存在的意义了。就可以如下图所示,把公式的 U U U 变成 m × n m\times n m×n、 Σ \Sigma Σ 变成一个方阵 n × n n\times n n×n。也就是说,可以将 Σ \Sigma Σ 的大小变成 M M M 的 m m m 和 n n n 最小值组成的方阵大小。在变成这种形式的时候, Σ \Sigma Σ 的奇异值是从大到小排列,在图中也就是颜色越深表示的奇异值越大。图中的五个奇异值代表的是它不同的基,如果将重要的轴方向保留,而次要方向的基给去掉,这样就实现了数据的压缩,在它压缩的时候,就能保留最多的信息。

我们在奇异值分解的时候,可以取前几个奇异值。这里假设将最后的奇异值去掉的时候,对原始矩阵的影响是比较小的,因为相对只是去掉了一个奇异值比较小的部分。

还可以把它再压缩,如只取前三个的情况。
综上,如果取前 r r r 个奇异值,那么 SVD 分解可以被写成下图的形式:

这种形式代表的是,我们可以把 U U U 矩阵的列拿出来,而 V V V 矩阵转置了,所以拿出来的是 V V V 的行向量。

使用向量乘法,可以得到一个个秩为 1 1 1 的矩阵(行向量都是相同的,这样秩还能不为 1 1 1 嘛):

再让奇异值乘进来,假定奇异值代表一种透明度然后将它叠起来,这样形成的东西就是原始矩阵 M M M 了。奇异值分解代表的就是这个含义,可以把它拆成三种模式的叠加,比如说 M M M 矩阵,可以让它的横的方向代表空间(如一条路的车辆是多少),纵方向代表时间,这样就构成了一个时间和空间的矩阵。它的SVD分解代表的意义也是可以拆分开成三种模式的叠加,如下图所示:
 这里先单独拿第一种模式来看,依旧是 u \mathbf{u} u 向量乘以 v \mathbf{v} v 向量再乘以 σ \sigma σ,这样构成出来的模式1与原始的时空矩阵大小是一样的,但它又服从一个非常简单的规律,即 u \mathbf{u} u 乘以 v \mathbf{v} v。
这里先单独拿第一种模式来看,依旧是 u \mathbf{u} u 向量乘以 v \mathbf{v} v 向量再乘以 σ \sigma σ,这样构成出来的模式1与原始的时空矩阵大小是一样的,但它又服从一个非常简单的规律,即 u \mathbf{u} u 乘以 v \mathbf{v} v。
 现在将这两个向量拿出来,就可以看到这种模式对应的一个时间分布情况及空间的分布情况。这里的空间单元可以是栅格可以是OD或者哪条路,这取决于要分析的是什么,时间可以是每天或每小时的一个数据。
现在将这两个向量拿出来,就可以看到这种模式对应的一个时间分布情况及空间的分布情况。这里的空间单元可以是栅格可以是OD或者哪条路,这取决于要分析的是什么,时间可以是每天或每小时的一个数据。
 那么就是原始的时空矩阵,等于第一种模式加上第二种模式再加上第三种模式。如果只保留前三种,它重构出来的矩阵已经非常接近原始矩阵,这时候相当于我们可以对原始的时空矩阵分解为几种重要的模式,而这三种模式它的时间跟空间的分布都是不一样的。
那么就是原始的时空矩阵,等于第一种模式加上第二种模式再加上第三种模式。如果只保留前三种,它重构出来的矩阵已经非常接近原始矩阵,这时候相当于我们可以对原始的时空矩阵分解为几种重要的模式,而这三种模式它的时间跟空间的分布都是不一样的。

如何求SVD分解
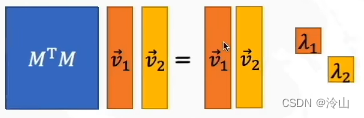
左边公式很好推就不做讲解了。这里引入特征向量的概念,如果我们对 M T M M^TM MTM 求特征向量,应该是 M T M v = λ v M^TM\mathbf{v}=\lambda \mathbf{v} MTMv=λv 的形式,得到的形式如下图所示:
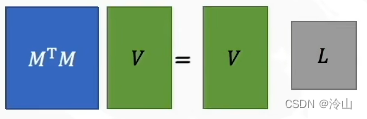
 然后将它移动一下,合并成 V V V,这就能得到 M T M V = V L M^TMV=VL MTMV=VL 这种形式。
然后将它移动一下,合并成 V V V,这就能得到 M T M V = V L M^TMV=VL MTMV=VL 这种形式。
 总结下SVD求解步骤:
总结下SVD求解步骤:
- 有公式 M = U Σ V T M=U\Sigma V^T M=UΣVT;
- 通过求 M T M M^TM MTM 的特征向量得到 V V V,同理通过求 M M T MM^T MMT 的特征向量得到 U U U;
- 求 M T M M^TM MTM 或 M M T MM^T MMT 的特征值,然后开方得到奇异值;
- 构成对角阵 Σ = [ σ 1 0 0 σ 2 ] \Sigma=\left[\begin{array}{llll}\sigma_1 & 0 \\ 0 &\sigma_2 \end{array}\right] Σ=[σ100σ2]
4. 主成分分析
假设我们有下图这样的一组数据,如果想把这个数据降维,PCA 就是找到一个新的坐标系,这个坐标系它的原点落在数据的中心,坐标系的方向往数据分布的方向,这样子相当于是可以把它降维。这时要存储的信息是,新的坐标系原点位置,以及新的坐标系相对于原来坐标系旋转的角度,然后再去存储它新的坐标点。这时点都分布在新坐标系的 x x x 轴上面,而新的坐标系 y y y 轴上的值都为 0 0 0,就不需要去存储了-------相当于是把二维的信息给降维到一维,即只需要存储一维新的 x x x 的坐标。
 图中为蓝色数据投影到轴上面,只保留一个维度时重新构建出的红色点数据。PCA 的目的就是找到一个坐标系使得这个数据在保留一个维度的时候,信息损失是最小的。
图中为蓝色数据投影到轴上面,只保留一个维度时重新构建出的红色点数据。PCA 的目的就是找到一个坐标系使得这个数据在保留一个维度的时候,信息损失是最小的。
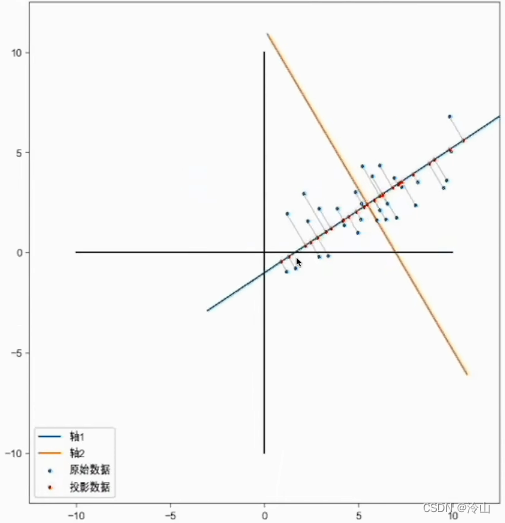

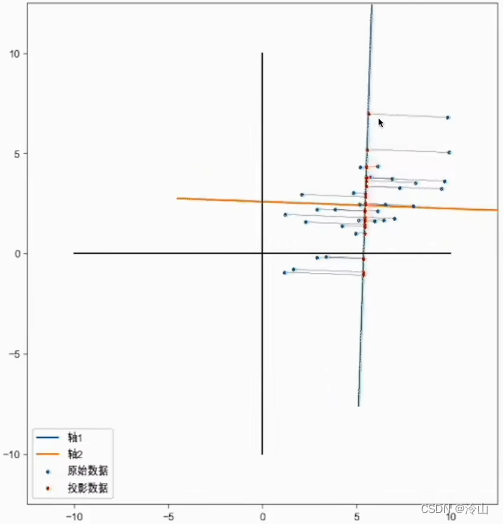
比如说转到下图这个位置的时候,它投影在轴上面,它的数据分布是最分散的,相当于是这个时候保留的信息是最多的。
比如说转到一个角度,将点投影上去,结果发现数据都集中在一个点,这相当于没有保存什么信息,数据并不能很好地在新的轴上面区分开,那就不是一个好的坐标轴。既然 PCA 是找到一个新的坐标系,怎么样才算是一个很好的坐标系?

如果我们能够找到一个新坐标系的方向,这个坐标系的第一个维度叫做主成分一;第二个维度叫做主成分二。如果我们找到数据在主成分一上面的投影的分布方差是最大的时候,那么说明主成分一它能够保留最多的信息,在这个时候这个方向就是最好的一个坐标系。
 那么怎么实现 PCA?
那么怎么实现 PCA?
- 首先,数据必须去中心化(把坐标轴原点放在数据中心)。假设没有把原点放在数据中心,可能发现不了最好的方向;
- 找坐标系,即找到方差最大的方向。
那么现在的问题就是,数据方差最大的方向是哪个方向呢?
4.2 白噪声
左边数据的分布的 x x x 轴跟 y y y 轴都是标准的正态分布,而且 x x x 和 y y y 不相关,也就是数据在 x x x 方向的分布是一个标准正态分布,即均值为 0 0 0、方差为 1 1 1; y y y 方向也是一个标准正态分布。
而手上的数据一般长右边这样,这是去中心化以后的(如后面PCA要讲的),即中心点在原点。该数据 x x x 和 y y y 都是正态分布,但不是标准的正态分布,其 x y xy xy 是相关的,也就是 x x x 方向变大的时候, y y y 方向也会变大。
 我们手上的数据是可以由创建的白数据做拉伸旋转得到。 D D D 左乘一个 S S S 做拉伸,再左乘一个 R R R 做旋转,就得到了 D ′ D' D′,就是后面要降维的数据。
我们手上的数据是可以由创建的白数据做拉伸旋转得到。 D D D 左乘一个 S S S 做拉伸,再左乘一个 R R R 做旋转,就得到了 D ′ D' D′,就是后面要降维的数据。
那么拉伸和旋转变换有什么作用?
这里拉伸的时候,就已经确定了拉伸的方向就是方差最大的方向,然后再旋转,旋转的角度决定了方差最大方向的角度是多大,所以要求的就是 R R R 矩阵,也就是转了多少度。如果能求出这个 R R R 的话,相当于是 PCA 问题就解决了。

刚才是从 D D D 把数据转换为手上的数据,而手上的数据 D ′ D' D′ 也可以转换回来,即取一个逆。

4.3 怎么求 R
协方差矩阵的特征向量就是 R R R。协方差矩阵表示的是,两个变量在变化过程中是同方向变化还是反方向变化,以及程度如何。自己跟自己的协方差,也就是方差。

数据在拉伸的时候,协方差也会发生改变。
 协方差矩阵刚好可以写成以下形式:
协方差矩阵刚好可以写成以下形式:
 而手上数据的协方差是 C ′ C' C′,将协方差矩阵带进去。因为白数据的协方差是单位矩阵,公式就可以化简为 R S S T R T RSS^TR^T RSSTRT,令 L = S S T L=SS^T L=SST,可以做进一步化简。
而手上数据的协方差是 C ′ C' C′,将协方差矩阵带进去。因为白数据的协方差是单位矩阵,公式就可以化简为 R S S T R T RSS^TR^T RSSTRT,令 L = S S T L=SS^T L=SST,可以做进一步化简。

那么手上数据的协方差的特征值跟特征向量的定义是什么?
其实就是 C ′ v = λ v C'\mathbf{v}=\lambda \mathbf{v} C′v=λv
 与 SVD 一样,特征向量1和特征向量2可以组成一个 R R R 矩阵,这就说明其实特征向量就是 R R R 矩阵。 R R R 矩阵是旋转角度,他的第一列就是这个特征向量 v 1 \mathbf{v_1} v1,为新坐标系的 x x x 轴的方向;第二列 v 2 \mathbf{v_2} v2 就是 y y y 轴的方向。
与 SVD 一样,特征向量1和特征向量2可以组成一个 R R R 矩阵,这就说明其实特征向量就是 R R R 矩阵。 R R R 矩阵是旋转角度,他的第一列就是这个特征向量 v 1 \mathbf{v_1} v1,为新坐标系的 x x x 轴的方向;第二列 v 2 \mathbf{v_2} v2 就是 y y y 轴的方向。
 我们手上的数据是 D ′ D' D′,如果对它成一个 R ′ R' R′,相当于是将它旋转回来,这时候数据的协方差是 L L L。在旋转回来之后, x x x 方向和 y y y 方向是不相关的, x x x 方向的方差是 a a a 平方, y y y 方向的是 b b b 平方。 a 2 a^2 a2 和 b 2 b^2 b2 是两个轴方向的方差,同时又是协方差矩阵的特征值。
我们手上的数据是 D ′ D' D′,如果对它成一个 R ′ R' R′,相当于是将它旋转回来,这时候数据的协方差是 L L L。在旋转回来之后, x x x 方向和 y y y 方向是不相关的, x x x 方向的方差是 a a a 平方, y y y 方向的是 b b b 平方。 a 2 a^2 a2 和 b 2 b^2 b2 是两个轴方向的方差,同时又是协方差矩阵的特征值。
 总结下PCA求解步骤:
总结下PCA求解步骤:
- 数据先去中心化:对原始数据每一列进行均值中心化,即将每个数据减去该列的均值;
- 计算协方差矩阵:将均值中心化后的数据按列组成一个 n × m n \times m n×m 的矩阵 X X X,其中 n n n 为样本数, m m m为原始数据的维度。然后计算该矩阵的协方差矩阵 C ′ = 1 n − 1 D ′ D ′ T C'=\frac{1}{n-1}D'D'^T C′=n−11D′D′T;
- 对协方差矩阵求特征向量和特征值。特征向量就是 R R R,就是旋转方向及坐标轴方向;特征值就是坐标轴方向上数据的方差。
- 选择主成分:将特征值从大到小排序,选择前 k k k 个特征值所对应的特征向量,其中 k k k 为降维后的目标维度。
- 映射到新空间:将原始数据 X X X 投影到选出的 k k k 个特征向量所张成的 k k k 维空间中,得到降维后的数据 Y Y Y。
4.4 PCA的缺点
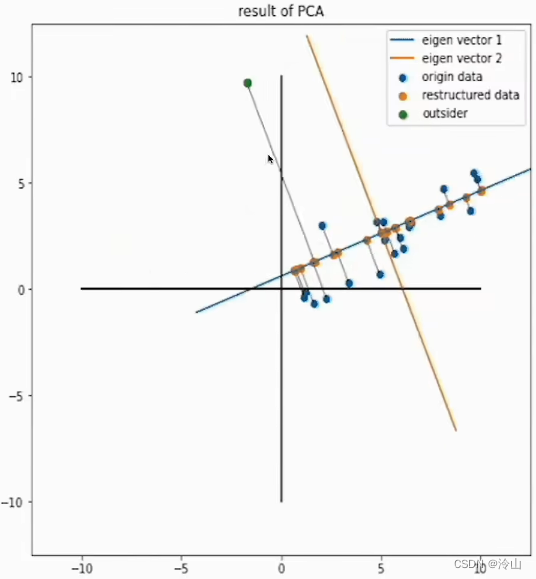
PCA的缺点是,离群点的影响大。下图绿色的点是加入的离群点,可以看见这里有 20 20 20 个数据,只是加了一个离群点,整个轴动的幅度很大,相当于它一个离群点就已经能够对 PCA 的结果造成很大的影响。这个也有其他降维的算法可以避免离群点的影响


5. PCA 的主成分与 SVD 的关系
SVD 中的右奇异矩阵2 V V V,就是 PCA 的主成分( R R R)。

PCA 需要先求出协方差矩阵,如果数据量和维度比较多的话,计算量可能很大。
以 SVD 的 V V V 矩阵作为 PCA 的主成分有两个好处:
- 一些 SVD 的实现算法可不求出协方差矩阵 C C C 也能求出右奇异矩阵 V V V(如迭代求解法),与 PCA 相比相当于是一个数据计算量的降低;
- PCA 仅仅使用了 SVD 的右奇异矩阵 V V V,没有使用到左奇异矩阵 U U U,那么 U U U 有什么用呢?详见 SVD 一节末尾处。
酉矩阵: n n n 阶复合矩阵 U U U 的 n n n 个列向量是 U U U 空间的标准正交基,则 U U U 是酉矩阵。(若 n n n 阶复矩阵 A A A 满足 A H A = A A H = E A^HA=AA^H=E AHA=AAH=E,则称 A A A 是酉矩阵,记作 A ∈ U n × n A\in U^{n\times n} A∈Un×n) ↩︎
奇异矩阵:不满秩的方阵。首先,看这个矩阵是不是方阵(即行数和列数相等的矩阵,若行数和列数不相等,那就谈不上奇异矩阵和非奇异矩阵)。如是方阵,再看此矩阵的行列式|A|是否等于0,若等于0,称矩阵A为奇异矩阵;若不等于0,称矩阵A为非奇异矩阵。由|A|≠0可知矩阵A可逆,这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵,非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵,则AX=0有无穷解,AX=b有无穷解或者无解。如果A为非奇异矩阵,则AX=0有且只有唯一零解,AX=b有唯一解。 ↩︎