一 特征值和特征向量
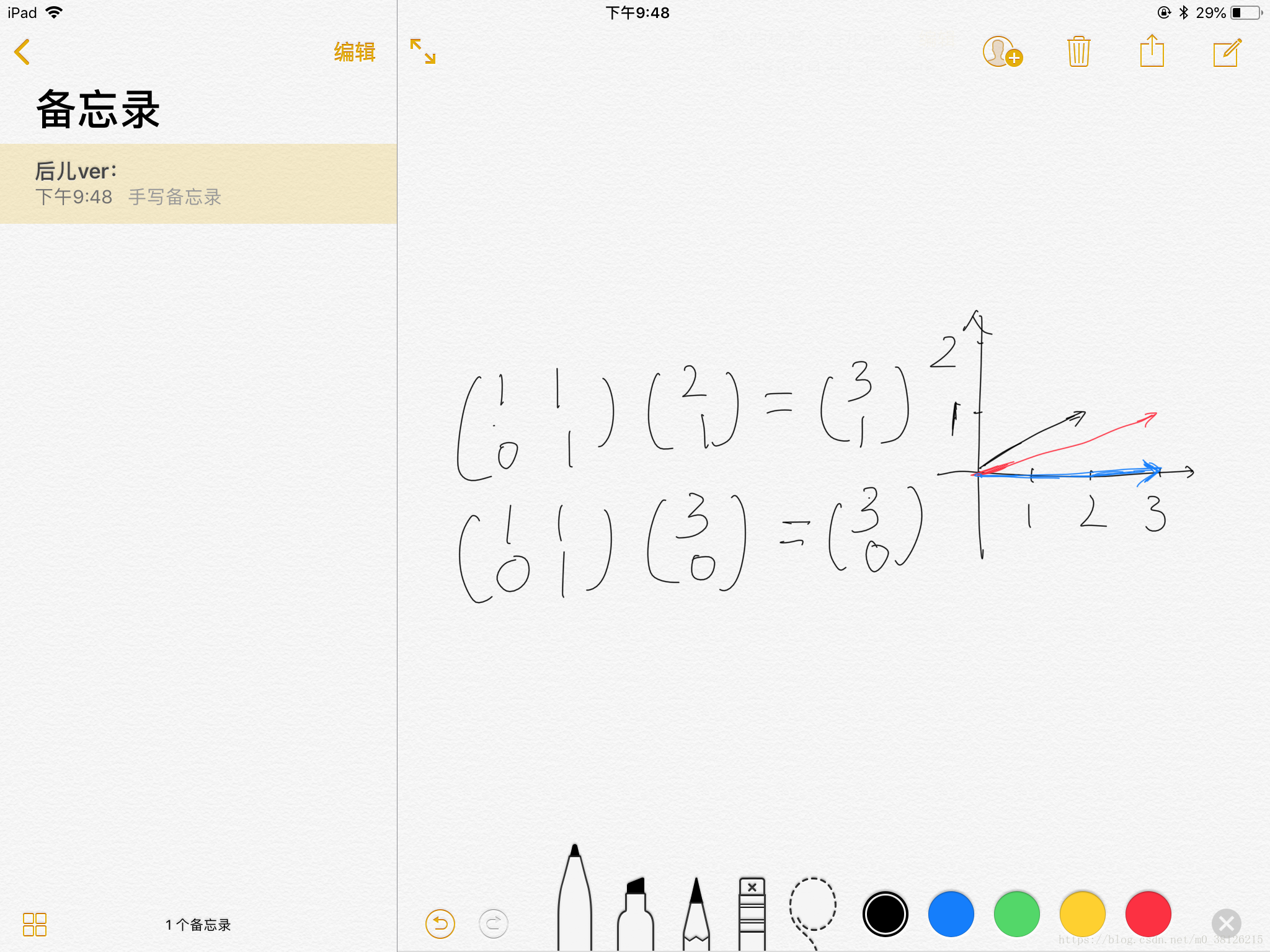
想了解PCA和SVD,首先要了解的一个概念就是特征值和特征向量。 A是矩阵,x是向量、
是数。如果满足公式,则说
是矩阵A的一个特征值,非零向量x为矩阵A的属于特征值
的特征向量。矩阵A的特征值和特征向量可以写成以下格式,请注意。
为什么能把x叫做A矩阵的特征向量呢,其实矩阵乘向量可以理解成对向量进行旋转和拉长。当然并不是所有向量都可以被旋转,矩阵无法旋转的非零向量就是该矩阵的特征向量!!
举一个不恰当的例子,当你想描述一部手机的时候,你会描述电池、屏幕和品牌等等手机的特征。现在轮到矩阵了,当你想描述一个矩阵的时候,不妨从它的特征向量入手。(降维可以简单理解成当矩阵的某个特征向量对应的特征值很小很小的时候,就可以抛弃这个特征向量了。)
| 手机 | 矩阵 | |
| 特征1 | 电池(3000毫安) | x1( |
| 特征2 | 屏幕(4寸) | x2( |
二 PCA
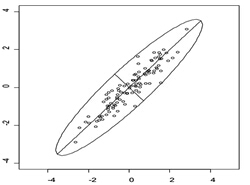
图解
如图所示,数据分布在一个椭圆内,每个点的坐标为(X1,Y1)。可以发现数据在椭圆长轴上分布的更开,代表在长轴上包含更多的信息。降维的思想就是抛弃短轴上的信息,保留下长轴的信息,每个点的坐标变为(aX1+bY1),二维信息就被降到了一维。
数学推导
1.PCA和特征值特征向量的关系
存在一组数据,xyz代表3个特征,n代表n个样本。现在想降维,就是减少特征的数量!
首先要明确一点,好的特征应该是相互之间没有相关关系的。例如,收入和可支配收入就是强相关的,两者都作为特征信息可能就冗余了。所以我们希望的降维之后的特征之间没有相互关系——即向量之间的协方差为0。
假设B是A转变后的矩阵,B=UA。转变后的B应该保证B的协方差矩阵为对角矩阵。
公式只看头尾就可以发现与特征值特征向量的公式关联上了。上述公式中涉及到了以下几个内容(选读)
1.想要协方差矩阵等于,必须对B各列先减去均值
完整的公式:
2.协方差矩阵是实对称矩阵,实对称矩阵的不同特征值相互正交,证明如下。
因为两个特征值不相等,想要等式成立必须x1和x2正交
3.由上文知道,协方差矩阵C是一个是对称矩阵,在线性代数上,实对称矩阵有一系列非常好的性质。1)实对称矩阵不同特征值对应的特征向量必然正交(已证明),2)设特征向量中质为r,则必然存在r个线性无关的特征向量对应于,因此可以将这r个特征向量单位正交化。只有单位正交矩阵U的专置才可以等于U的逆。
2.特征如何降维
B=UA,A维度是(3,n),U是由协方差矩阵的特征向量组成的维度是(3,3),这样计算出的B维度是(3,n),数据其实并没有降维。降维的关键就在于U,如果U是一个(2,3)的矩阵,那B就变成了(2,n)。是不是我们只挑选协方差矩阵的两个特征向量组成U就可以了,是的!!特征值按大小排序,选择前2个特征值的特征向量组成U即可。特征值的大小可以理解成包含信息的多少,小的特征值说明原矩阵在该特征向量上并没有多少信息,可以舍弃。
3.PCA — python
import numpy as np
from sklearn.decomposition import PCA
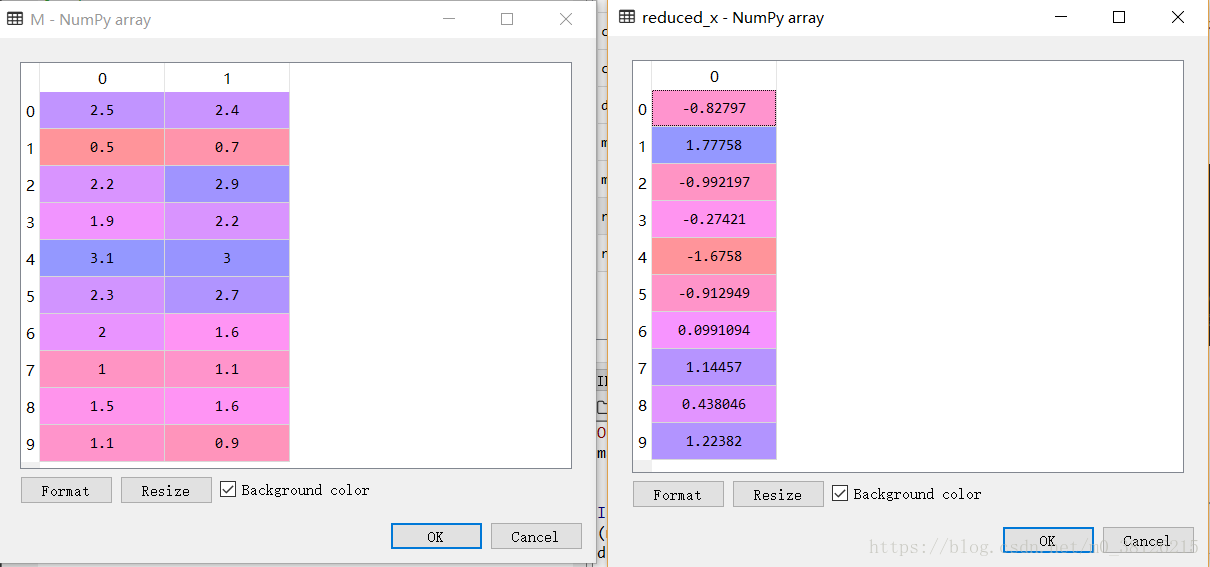
M = [[2.5,2.4],[0.5,0.7],[2.2,2.9],[1.9,2.2],[3.1,3.0],[2.3,2.7],[2,1.6],[1,1.1],[1.5,1.6],[1.1,0.9]]
M = np.mat(M)
pca=PCA(n_components=1) #加载PCA算法,设置降维后主成分数目为2
reduced_x=pca.fit_transform(M) #对样本进行降维二维数据成功被降为一维,见图。注意该数据每行是一个样本,与前期讨论的每列一个样本不一样。
下面手动实现PCA
meanVals=np.mean(M,axis=0) #对每一个特征求均值,这里是对列求
meanRemoved=M-meanVals # 原始数据减去均值
covMat=np.cov(meanRemoved.T) #计算协方差矩阵
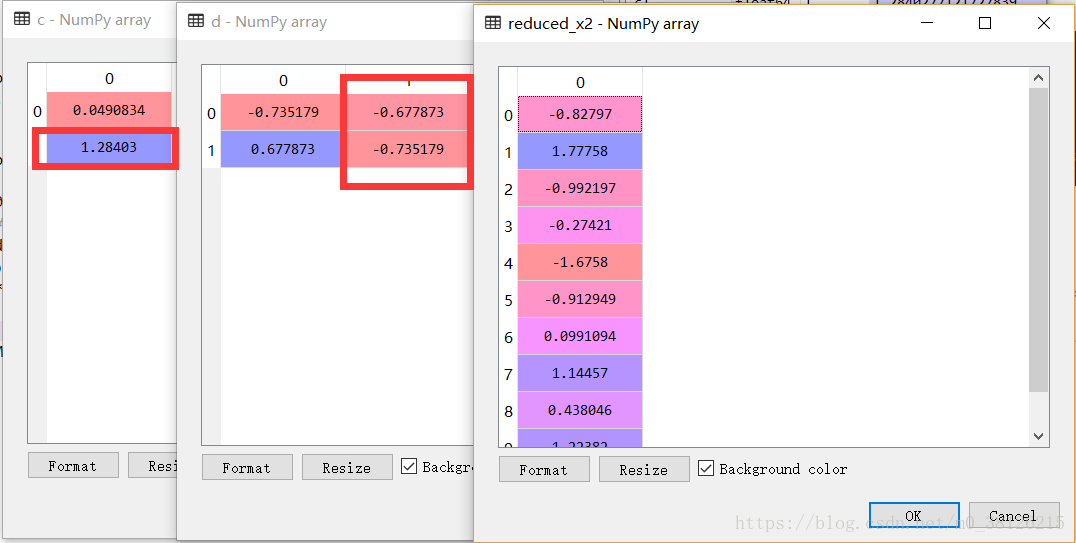
c,d=np.linalg.eig(covMat) #计算协方差矩阵的特征值和特征向量
reduced_x2 = meanRemoved*np.mat(d[:,1]).T # 挑选最大特征值对应的特征向量,用于数据降维挑选最大的特征值对应的特征向量(图中红框),用挑选出得特征向量对减去均值的原始数据处理。可以发现最终结果和PCA方法的结果一模一样。
参考了这个https://blog.csdn.net/xueli1991/article/details/69665887?locationNum=14&fps=1
三 SVD
1 SVD
方阵可以计算特征值和特征向量,那么非方阵呢?非方阵可以利用奇异值分解提取特征。
V和U都代表什么,UU分别是A*A.T和A.T*A的特征向量,而特征值就是A*A.T或A.T*A特征值的开方。
2.如何使用
我们可以通过选择前r个特征值与特征向量达到信息压缩,近似矩阵的目的。
例如在图片压缩上,1080*960=的图片在使用100特征值的情况下,可以有效的压缩成1080*100+100+100*960三个矩阵。
图片来源于https://blog.csdn.net/bluecol/article/details/45971423
其实在潜在语义搜索和推荐算法中,SVD都大有用处。
3 SVD — python
利用Numpy自带的方法进行奇异值分解
M = [[1,2,3,4],[5,6,7,8],[9,10,11,1],[2,3,4,5],[6,7,8,9]]
M = np.mat(M)
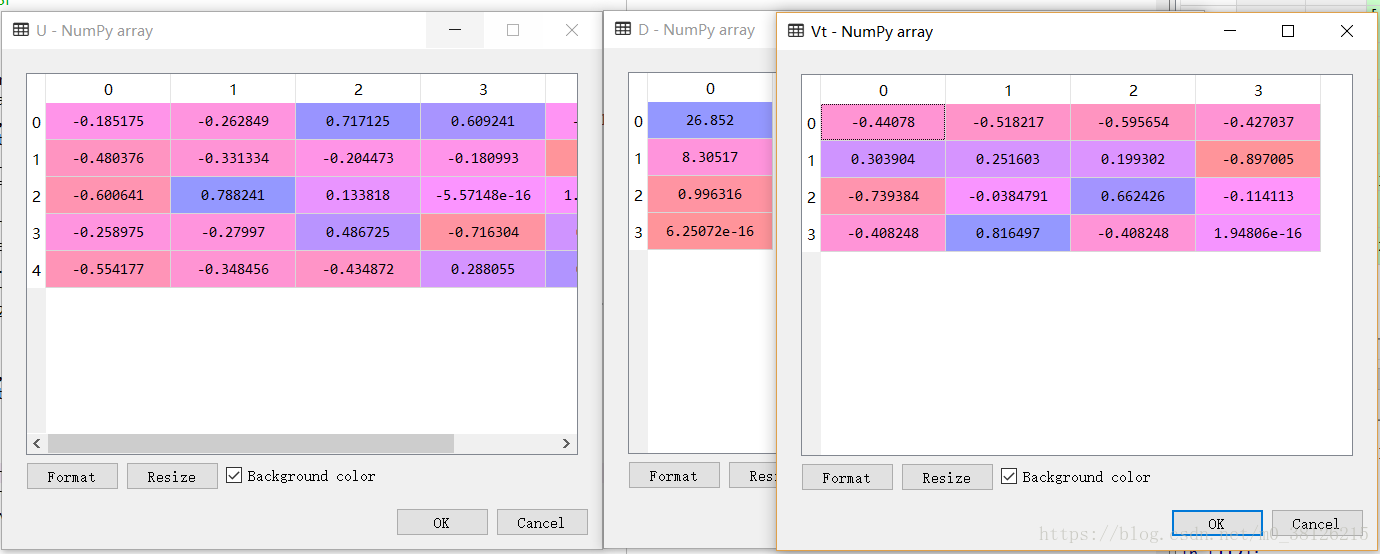
U, D,Vt = np.linalg.svd(M)结果如下
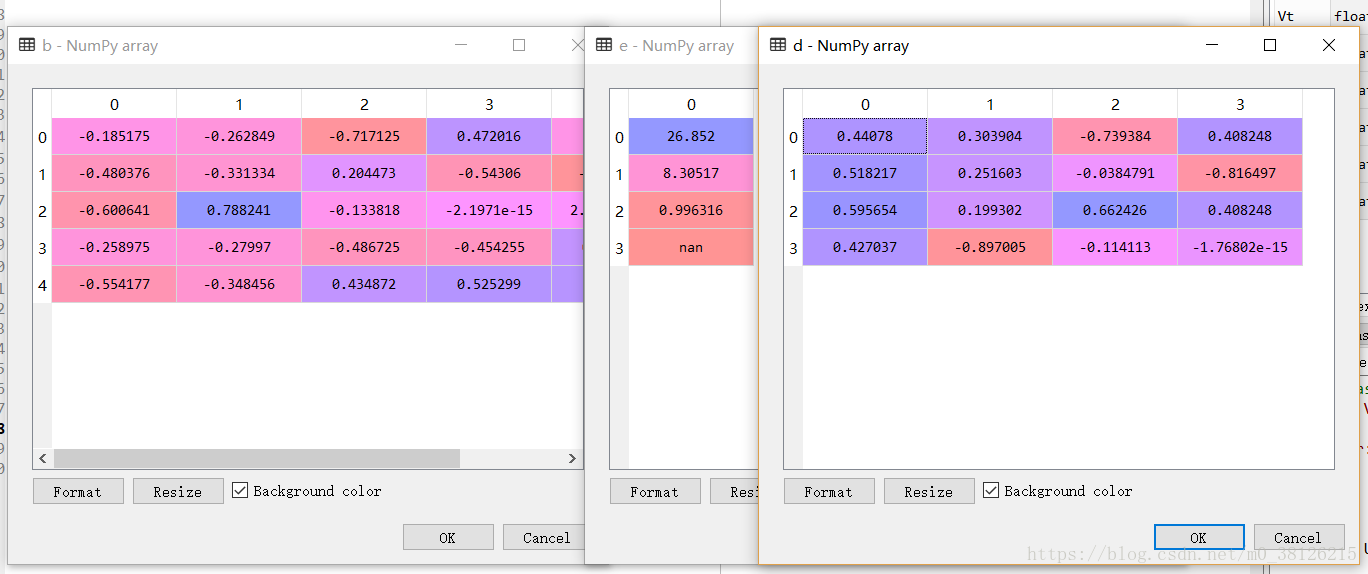
下面分别计算A*A.T和A.T*A的特征值和特征向量,b,e,d分别对应U,D,V
a,b=np.linalg.eig(M*M.T)
c,d=np.linalg.eig(M.T*M)
e = np.power(c,1/2)四 总结
| 计算方法 | 目的 | 应用 | |
| PCA | 首先计算特征的协方差矩阵的特征值和特征向量,利用特征值的大小对特征向量进行筛选。最终用筛选出得特征向量和原矩阵(减去均值后的)相乘,结果就是降维后的数据 | 对样本的特征进行重新组合,降维。 | 降维后的数据可以用于各种监督学习的算法,减少计算量,提高计算结果的质量。 |
| SVD | 将非方阵矩阵拆分开 | 图片压缩、推荐系统和语义搜索等等 |
简单提一下另一个特征降维的算法——因子分析。PCA是想方设法将特征组合,而因子分子想方设法将特征拆分。例如语文,数学,物理,化学,生物,地理成绩可能会被因子分析拆成记忆力能力、计算能力、写作能力等等。对于因子分析,可以使用旋转技术,使得因子更好的得到解释,因此在解释主成分方面因子分析更占优势,因子分析以后有机会再介绍吧。