奇异值分解SVD 原理+作业

奇异值分解SVD 原理+作业

1. 简介

1.1 简介

矩阵分解在机器学习领域有着广泛应用，是降维相关算法的基本组成部分。

矩阵分解的定义

把一个矩阵表示成多个矩阵连乘的形式。

矩阵分解主要有两个作用

1. 分解后的每个小矩阵能够更容易的求逆
2. 分解后的每个小矩阵有特殊的物理意义

常见的矩阵分解方式有以下两种

1. 特征分解Eigendecomposition, 也叫作谱分解Spectral decomposition

2. 奇异值分解Singular Value decompositon（SVD）

特征值分解是一个提取矩阵特征很不错的方法，可是它只是对方阵而言的，在现实的世界中，咱们看到的大部分矩阵都不是方阵，好比说有$N$个学生，每一个学生有$M$科成绩，这样造成的一个$N\times M$的矩阵就不多是方阵，咱们怎样才能描述这样普通的矩阵呢的重要特征呢?奇异值分解能够用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法:

想要理解SVD，必须理解的数学知识

1.2 正交变换

正交变换公式
$$X=UY$$
上式表示:$X$是$Y$的正交变换，其中$U$是正交矩阵，$X$和$Y$为列向量。

下面用─个例子说明正交变换的含义∶

假设有两个单位列向量$a$和$b$，两向量的夹角为$\theta$，如下图:

现对向量a，b进行正交变换：
$$\begin{gathered} {\vec{a}}^{\prime }=U\cdot \vec{a} \\ {\vec{b}}^{\prime }=U\cdot \vec{b} \end{gathered}$$
${\vec{a}}^{\prime },{\vec{b}}^{\prime }$的模：
$$\begin{gathered} ||{\vec{a}}^{\prime }||=||U\cdot \vec{a}||=||U||\cdot ||\vec{a}||=||\vec{a}||=1 \\ ||{\vec{b}}^{\prime }||=||U\cdot \vec{b}||=||U||\cdot ||\vec{b}||=||\vec{b}||=1 \end{gathered}$$
由上式可知${\vec{a}}^{\prime },{\vec{b}}^{\prime }$的模为1

${\vec{a}}^{\prime }$和${\vec{b}}^{\prime }$的内积为
$$\begin{gathered} {{\vec{a}}^{\prime }}^T\cdot {\vec{b}}^{\prime }=(U\cdot \vec{a}{)}^T\cdot (U\cdot \vec{b})={\vec{a}}^T{U}^{T}U\vec{b} \\ \Rightarrow {{\vec{a}}^{\prime }}^T\cdot {\vec{b}}^{\prime }={\vec{a}}^T\cdot \vec{b} \end{gathered}$$
由上式可知，正交变换前后的内积相等。

${\vec{a}}^{\prime }$和${\vec{b}}^{\prime }$的夹角${\theta }^{\prime }$
$$\begin{gathered} \cos {\theta }^{\prime }=\frac{{{\vec{a}}^{\prime }}^T\cdot {\vec{b}}^{\prime }}{||{{\vec{a}}^{\prime }}^T||\cdot ||{\vec{b}}^{\prime }||} \\ \cos \theta =\frac{{\vec{a}}^T\cdot \vec{b}}{||{\vec{a}}^T||\cdot ||\vec{b}||} \end{gathered}$$
正交变换前后的夹角相等，即${\theta }^{\prime }=\theta$

因此，正交变换的性质可用下图来表示：

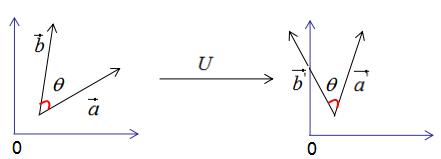
正交变换的两个重要性质：

1）正交变换不改变向量的模。

2）正交变换不改变向量的夹角。

如果向量$\vec{a}$和$\vec{b}$是基向量，那么正交变换的结果如下图：

基向量正交变换后的结果仍是基向量 。基向量是表示向量最简洁的方法，向量在基向量的投影就是所在基向量的坐标，我们通过这种思想去理解特征值分解和推导SVD分解。

正交变换只是将变换向量用另一组正交基表示，在这个过程中并没有对向量做拉伸，也不改变向量的空间位置，假如对两个向量同时做正交变换，那么变换前后这两个向量的夹角显然不会改变。

1.3 特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下：
$$Ax=\lambda x$$
$A$是一个$n\times n$的矩阵，$x$是一个$n$维向量，则我们说$\lambda$是矩阵$A$的一个特征值，而$x$是矩阵$A$的特征值$\lambda$所对应的特征向量。

求出特征值和特征向量有什么好处呢？

我们可以将矩阵$A$特征分解，如果我们求出了矩阵$A$的$n$个特征值${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$，以及这$n$个特征值对应的特征向量 { w 1 , w 2 , ⋯   , w n } \{w_1,w_2,\cdots,w_n\} { w1​,w2​,⋯,wn​},如果这$n$个特征向量线性无关，那么矩阵$A$就可以用下式的特征分解表示
$$A=W\Sigma W^{-1}$$
其中$W$是这$n$个特征向量所张成的$n\times n$维矩阵，而$\Sigma$为这$n$个特征值为主对角线的$n\times n$维矩阵。

为了可视化特征值分解，假设$A$是$2\times 2$的对称矩阵，$U=(u_1,u_2),\Sigma =({\lambda }_1,{\lambda }_2)$。把上式展开
$$\begin{gathered} A{u}_1={\lambda }_1{u}_1 \\ A{u}_2={\lambda }_2{u}_2 \end{gathered}$$
用图形表示为

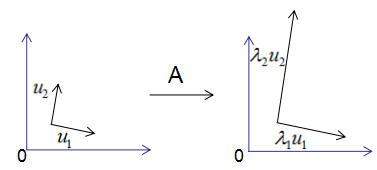
由上图可知，矩阵A没有旋转特征向量，它只是对特征向量进行了拉伸或缩短（取决于特征值的大小），因此，对称矩阵对其特征向量（基向量）的变换仍然是基向量（单位化） 。

特征向量和特征值的几何意义：若向量经过矩阵变换后保持方向不变，只是进行长度上的伸缩，那么该向量是矩阵的特征向量，伸缩倍数是特征值。

一般我们会把$W$的这个$n$个特征向量标准化，即满足$||w_i|{|}_2=1$,或者说$w_i\cdot w_i^T=1$.此时$W$的$n$个特征向量为标准正交基。满足$W^{T}W=I$，即$W^T=W^{-1}$，也就是说$W$为酉矩阵，在实数矩阵中，酉矩阵指的是转置矩阵与逆矩阵相等的矩阵；在复数矩阵中，酉矩阵指的是共轭转置矩阵（矩阵中各元素实部不变，虚部相反数）与逆矩阵相等的矩阵。

这样我们的特征分解表达式可以写成:
$$A=W\Sigma W^T$$
注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

1.4 SVD

假设$A$是一个$m\times n$的矩阵，那么可以定义$A$的SVD为
$$A=U\Sigma V^T$$
其中,${\Sigma }_{m\times n}$对角矩阵，主对角线上的元素为奇异值，$V_{n\times n}$和$U_{m\times m}$都是酉矩阵，即满足$U^{T}U=I,V^{T}V=I$

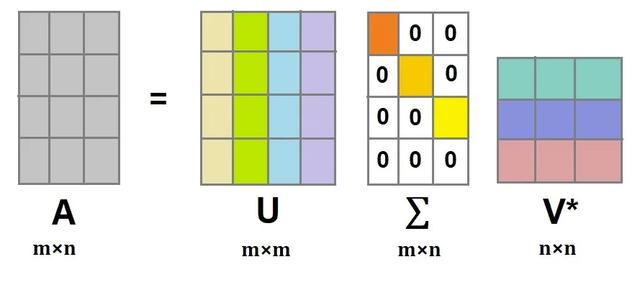
证明如下

先回顾一下正交变换的思想：基向量正交变换后的结果仍是基向量 。

我们用正交变换的思想来推导SVD分解：

假设$A$是$M\times N$的矩阵，秩为$K$，$Rank(A)=k$。

存在一组正交基V：
$$V=(v_1,v_2,\cdots ,v_k)$$
矩阵对其变换后仍是正交基，记为$U$：
$$U=(A{v}_1,A{v}_2,\cdots ,A{v}_k)$$
由正交基定义，得：
$$(A{v}_i{)}^T(A{v}_j)=0$$
上式展开：
$$v_i^T{A}^{T}A{v}_j=0$$
如果我们将$A^T$和$A$做矩阵乘法，那么会得到$n\times n$的一个方阵$A^{T}A$.既然$A^{T}A$是方阵，那么我们就可以进行特征分解，得到特征向量$v_i$和特征向量$\lambda$。当$v_i$是$A^{T}A$的特征向量时，有：
$$(A^{T}A)v_i=\lambda v_i$$
根据$v_i^T{A}^{T}A{v}_j=0$,得到
$$\lambda v_i^T{v}_j=0$$
即假设成立 。

图形表示如下：

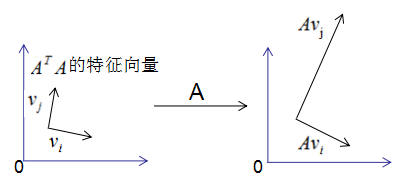
正交向量的模：
$$\begin{gathered} ||A{v}_i|{|}^2=(A{v}_i{)}^T(A{v}_i) \\ \Rightarrow ||A{v}_i|{|}^2=v_i^T{A}^{T}Av \\ \Rightarrow ||A{v}_i|{|}^2={\lambda }_i{v}_i^{T}v={\lambda }_i \\ \therefore ||A{v}_i|{|}^2=\sqrt{{\lambda }_i} \end{gathered}$$
单位化正交向量，得：
$$\begin{gathered} u_i=\frac{A{v}_i}{||A{v}_i}=\frac{1}{\sqrt{{\lambda }_i}}A{v}_i \\ \Rightarrow A{v}_i=\sqrt{{\lambda }_i}{u}_i \end{gathered}$$
结论：当基向量是$A^A$的特征向量时，矩阵A转换后的向量也是基向量 。用矩阵的形式表示为
$$AV=U\Sigma$$
其中$V=(v_1,v_2,\cdots ,v_k),\Sigma =\left[\begin{array}{cccc}{\sigma }_1& & & \\ & {\sigma }_2& & \\ & & \ddots & \\ & & & {\sigma }_k\end{array}\right],U=(u_1,u_2,\cdots ,u_k),{\sigma }_i=\sqrt{{\lambda }_i}$

V是$N\ast K$矩阵，U是$M\ast K$矩阵,$\Sigma$是M*K的矩阵，需要扩展成方阵形式：
$$AV=U\Sigma$$
两式右乘$V^T$可得矩阵的奇异值分解
$$A=U\Sigma V^T$$

2. 流程

用一个简单的例子来说明矩阵是如何进行奇异值分解的。矩阵A定义为：
$$A=\left[\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right]$$
首先求出$A^{T}A$和$A{A}^T$
$$\begin{gathered} A^{T}A=\left[\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right]\left[\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right] \\ A{A}^T=\left[\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right]=\left[\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right] \end{gathered}$$
求$A^{T}A$的特征向量$V$和特征值$\lambda$
$$V=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$$
对应的特征值为${\lambda }_1=3,{\lambda }_2=1$，对应的平方根${\sigma }_1=\sqrt{3},{\sigma }_2=1$

求$A{A}^T$的特征向量$U$
$$U=\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}}& 0& -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\end{array}\right]$$
所以$A$的奇异值分解
$$A=\left[\begin{array}{ccc}\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\\ \frac{2}{\sqrt{6}}& 0& -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}\end{array}\right]\left[\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]$$

3. 作业

3.1 手动实现SVD

要求

根据课堂讲授的SVD分解方法，用 Python 语言编程实现矩阵的SVD 分解和 thin SVD 表达。

要求：

代码要有规范的注释, 输出以下两个测试例的结果
$$A=\left[\begin{array}{ccccc}1& 0& 0& 0& 2\\ 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 4& 0& 0& 0\end{array}\right]$$

第二个
$$A=\left[\begin{array}{cc}2& 0\\ 0& \frac{1}{\sqrt{2}}\\ 0& \frac{-1}{\sqrt{2}}\end{array}\right]$$

代码

import numpy as np


def get_data2():
    return np.array([[2, 0],
                     [0, 1 / np.sqrt(2)],
                     [0, 1 / np.sqrt(2)], ])


def get_data():
    return np.array([[1, 0, 0, 0, 2],
                     [0, 0, 3, 0, 0],
                     [0, 0, 0, 0, 0],
                     [0, 4, 0, 0, 0]])


def get_eigenvalue(A):
    return np.linalg.eigvals(A)


def get_U(A):
    return np.linalg.eig(A.dot(A.T))


def get_V(A):
    return np.linalg.eig(A.T.dot(A))


def SVD():
    sigma, V = get_V(A)
    sigma, V, length = bubble_sort(sigma, V)
    sigma2, U = get_U(A)
    sigma, U, _ = bubble_sort(sigma2, U)
    S = np.zeros((m, n))
    for i in range(length):
        S[i][i] = np.sqrt(sigma[i])

    # print(S)
    # U = np.zeros((m, m))
    # print(U.shape)
    for i in range(length):
        # print((1 / np.sqrt(sigma[i])) * np.dot(A, V[:, i]))
        U[:, i] = (1 / np.sqrt(sigma[i])) * np.dot(A, V[:, i])
    return U, S, V


def bubble_sort(sigma, B):
    """
    对奇异值进行排序
    :param sigma:
    :param B:
    :return:
    """
    length = len(sigma)
    for i in range(length - 1):
        # i表示比较多少轮
        for j in range(length - i - 1):
            if sigma[j] < sigma[j + 1]:
                sigma[j], sigma[j + 1] = sigma[j + 1], sigma[j]
                B[:, [j, j + 1]] = B[:, [j + 1, j]]
    temp = 0
    for i in range(length):
        if sigma[i] > 0:
            temp = temp + 1
    return sigma, B, temp


# 获取数据
A = get_data2()
m = A.shape[0]
n = A.shape[1]
k = min(m, n)

U, S, V = SVD()
temp2 = np.dot(np.dot(U, S), V.T)
print("SVD-- \n U=\n{}\n Z=\n{}\n V=\n{}".format(U, S, V))
print("*" * 10)
print(temp2)

结果

SVD-- 
 U=
[[ 1.          0.          0.        ]
 [ 0.          0.70710678  0.70710678]
 [ 0.          0.70710678 -0.70710678]]
 Z=
[[2. 0.]
 [0. 1.]
 [0. 0.]]
 V=
[[1. 0.]
 [0. 1.]]
**********
[[2.         0.        ]
 [0.         0.70710678]
 [0.         0.70710678]]

3.2 人脸识别

要求

作业2：实现基于奇异值分解的人脸识别。

要求：

1. 提交可运行的python源码（包括数据集、运行代码、运行结果)。
2. 撰写WORD文档，说明与分析所用人脸识别方法、原理，实现，测试

数据集介绍

数据集如下:ORL数据集

目录结构如下

数据集下载

我自己上传的 ORL数据集attrface | Kaggle

官网网址，貌似不能用了https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html

代码

# 人脸识别是一个分类问题
# svc 支持向量解决分类问题
import cv2
import numpy as np
import os

data_path = r"att_faces"
train_data = []
test_data = []
image = []
sigma_data = []

# 使用50个特征值作为该图像的特征信息
K = 80
print("选取了{}个特征".format(K))


def read_image():
    """
    加载图片信息
    :return:
    """
    global train_data, test_data
    root_path = os.listdir(data_path)
    for d in root_path:
        s_path = os.path.join(data_path, d)
        for idx, image_path in enumerate(os.listdir(s_path)):
            # 因为是二维图,所以是二维的 [112,92]
            img = cv2.imread(os.path.join(s_path, image_path), cv2.IMREAD_GRAYSCALE)
            image.append(img)
    train_data = image[0::2]
    test_data = image[1::2]


def train():
    """
    进行训练,训练的目的就是把40 张图片的所有 特征值提取出来，放进sigma_data
    :return:
    """

    for image in train_data:
        # 数据进行展示
        u, sigma, v = np.linalg.svd(image)
        # 对sigma 从小到大排序
        sigma = np.sort(sigma)
        # 选取特征值K个最大特征值作为Sm_i的特征值
        sigma_data.append(sigma[-K:])

    print("训练结束")


def test():
    """
    用提前准备好的图片 做最近邻算法的比较,和谁的最近邻 小

    :return:
    """
    # 分类正确的个数
    acc = 0
    for idx, image in enumerate(test_data):
        u, sigma, v = np.linalg.svd(image)
        # 对sigma 从小到大排序
        sigma = np.sort(sigma)
        # 选取特征值K个最大特征值作为Sm_i的特征值
        sigma = sigma[-K:]
        m = get_index(sigma)
        raw = int(idx / 5) + 1
        predict = int(m / 5) + 1
        if raw == predict:
            acc += 1
            print("这张图预测为{},预测正确".format(predict, raw))
        else:
            print("这张图预测为{},预测错误,本来是{}".format(predict, raw))

    print("最终准确率{}%,--[{}/{}]".format(100 * acc / len(test_data), acc, len(test_data)))
    # 使用


def get_index(sigma):
    """
    求出最小近邻的 所在是索引值
    :param sigma: 测试图像的前 K 个最大特征值
    :return:
    """
    index = []
    for i in sigma_data:
        # 最小近邻，其实就是求第二范数
        index.append(np.linalg.norm(i - sigma))
    return np.argmin(index)


# 加载数据
read_image()
# print(test_data)

# 训练
train()
# 测试
test()

结果如下

这张图预测为21,预测错误,本来是38
这张图预测为38,预测正确
这张图预测为39,预测正确
这张图预测为39,预测正确
这张图预测为39,预测正确
这张图预测为39,预测正确
这张图预测为39,预测正确
这张图预测为34,预测错误,本来是40
这张图预测为40,预测正确
这张图预测为40,预测正确
这张图预测为40,预测正确
这张图预测为40,预测正确
最终准确率73.0%,--[146/200]

参考资料

奇异值分解（SVD）原理总结_小白学视觉的博客-CSDN博客

奇异值分解（SVD）原理总结 (360doc.com)

奇异值分解(SVD)原理 - JavaShuo