贝叶斯滤波详解
贝叶斯滤波的用途(Bayesian Filtering):
贝叶斯滤波理论的应用可谓十分广泛。我们知道,在机器人运动过程中,有两个方面的信息来源,一个是通过我们实际控制机器人的运动路线(状态方程)和机器人传感器观测的实际信息(观测方程)来估计自身的位姿,但实际上,无论是状态还是观测都不可避免的存在噪声。假如机器人单方面的仅通过状态方程或观测方程来估计自身位姿,这样一来随着时间的不断推移,机器人估计的位姿与机器人实际的位姿误差将会越来越大。这时候我们就需要考虑这样一个问题:如何有效的融合控制信息和观测信息(状态方程和观测方程,即对同一状态的不同估计)从而减小机器人估计自身位姿的不确定度,这时候贝叶斯滤波理论就派上用场了。
贝叶斯滤波理论简介:
通过贝叶斯公式对随机信号进行处理,减小噪声带来的不确定性。
接下来,我们将从贝叶斯公式出发,从零开始一步步理解贝叶斯滤波。
贝叶斯学派
在统计学中,贝叶斯学派是区别于频率学派的又一大派别。我们高中所学的概率统计是基于频率学派思想,频率学派认为,一个事件的概率是可以通过大量重复实验下的事件出现的频率来给出(基于大数定理),且该事件的概率不依赖于主观判断给出的概率。(举个例子,比如有一个人拿一枚硬币,根据之前的某种经验,他认为正面朝上的概率是0.7,那么对于是否要把0.7的概率作为将来计算正面朝上的概率的一个参考,频率学派持反对意见,而贝叶斯学派则恰恰相反,他们认为主观的经验反倒有借鉴意义)

事实上,贝叶斯学派的思想在现如今得到人们的青睐还有一个更重要的原因:那就是许多事情无法进行大量的重复实验(随机实验)因为每一次重复实验都应有一个前提,那就是实验的条件应该严格相同或至少大致相同。然而现实生活中大多数情况都不具备如此理想的条件。比如天气预测,股市分析,当然也包括机器人的姿态估计。
(转化为数学描述就是频率派眼中的概率符合大数定律,样本x1,x2,…,xk之间相互独立,互不干扰。而生活中的很多情况是随机过程,彼此之间相互关联,无法依赖于大量重复的随机实验进行预测)
贝叶斯学派进行概率估计的时候将人们的主观经验称为先验概率,在主观经验的基础上得到某个结果的概率叫做似然概率,而将那个结果作用于先验信息,最终更新先验概率得到的预测结果的概率叫做后验概率(会不会有点绕,没事,我接下来举个例子就能慢慢理解了)
贝叶斯公式
我们通过一个例子给出贝叶斯公式:
比如我们这时候想要测温度,通过某种经验(比如往年今日的气温)得出今天可能的气温概率如下:
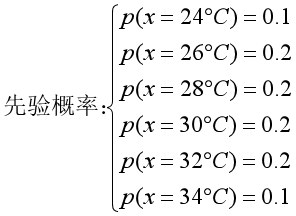
而此时,温度计的读数显示是29度(由于温度计也有误差,因此观测结果也不是绝对准确的)。
这时候,根据以上信息,如果我们要估计今天是30度的概率,该如何估计呢?
这时候便引入贝叶斯公式:

其中:
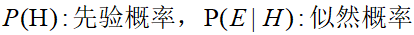
而对于P(E),我们可以这样理解:
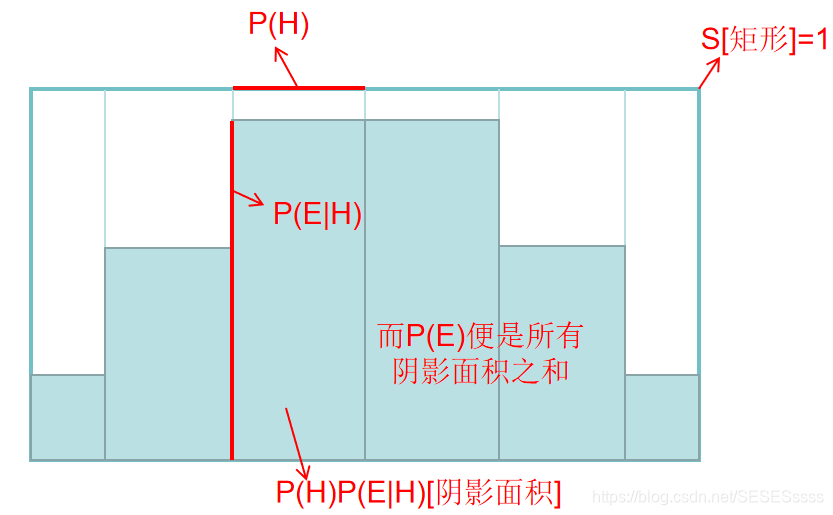
因此,P(E)与H的取值无关,而与H的分布率有关。
所以P(E)也可以表示一个常数,即:
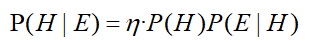
那么我们的估计,用贝叶斯公式表示就是:

连续随机变量下的贝叶斯公式
详细推导过程:
相较于上部分的概率分布是离散的形式,我们再来推导一下连续随机变量下的贝叶斯公式:
(Y,X是连续随机变量,概率服从一定的分布函数)
但我们不能直接使用类推,简单想想:由于是连续随机变量,因此对于每一个具体取值的概率都将趋于0.
这时候我们可以将取值先化为一个具体的区间,即先求P(X<x|Y=y),并转化为求和,则有:
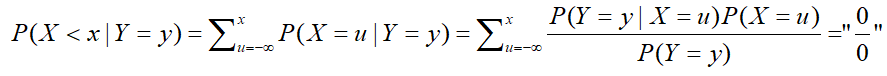
但实际上,分子和父母都是趋于0,这就成了一个0/0型,但这并不是求极限,我们也不能使用洛必达(汗)
同样的思想,再将概率中的取值转化为一个区间,只不过这次是一个极小的区间,看看能不能约掉什么:
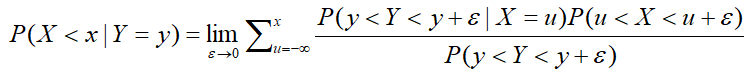
利用积分的思想,将小区间下的概率转化为密度函数在小区间上的积分(其中f是概率密度函数),即:
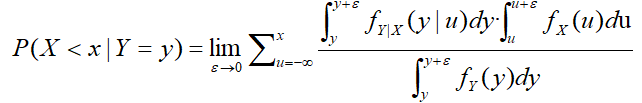
再运用中值定理,有:
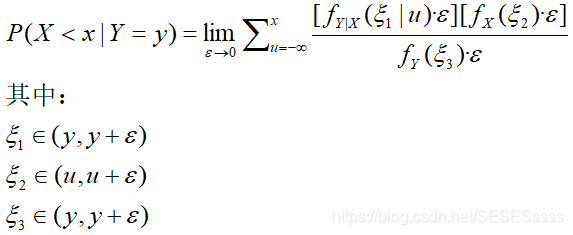
由于epsilon趋于0,那么可以将xi1,xi2,xi3近似为y,u,y,再约去epsilon:
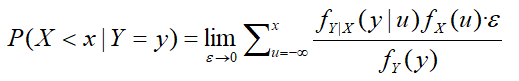
通过观察,这是一个无穷小求和形式,我们可以将其转化为积分的形式:
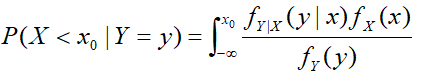
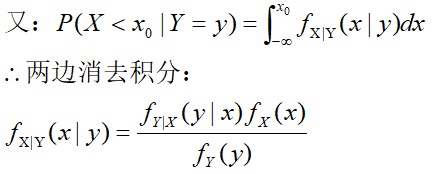
最后这便是连续随机变量下的贝叶斯公式,(发现和贝叶斯公式挺像的,只不过将概率换成了概率密度函数)
那么我们是否也可以将其写成[先验]*[似然]最后乘上一个常数的形式呢?
可以的,因为:
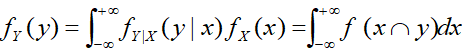
再用那个矩形想一想,就是阴影面积之和,且由于实际公式中只有x是变量(最终出来是关于x的分布),观测值y是已知的,所以fY(y)最终积出来就是一个常数,即:
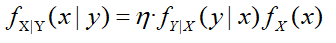
同样是测温度的例子:
假设今天的气温符合N(30,1)的正态分布(先验):
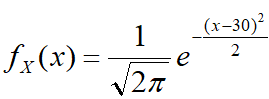
温度计读数为29度。(这里还需考虑传感器精度,假设传感器精度为土0.2°C)(似然):
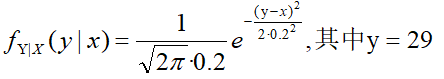
(后验):
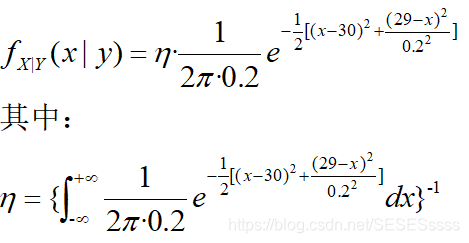
最终结果(计算过程略):
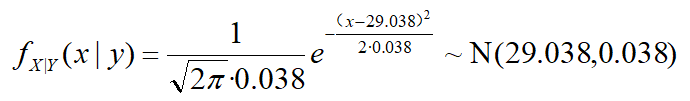
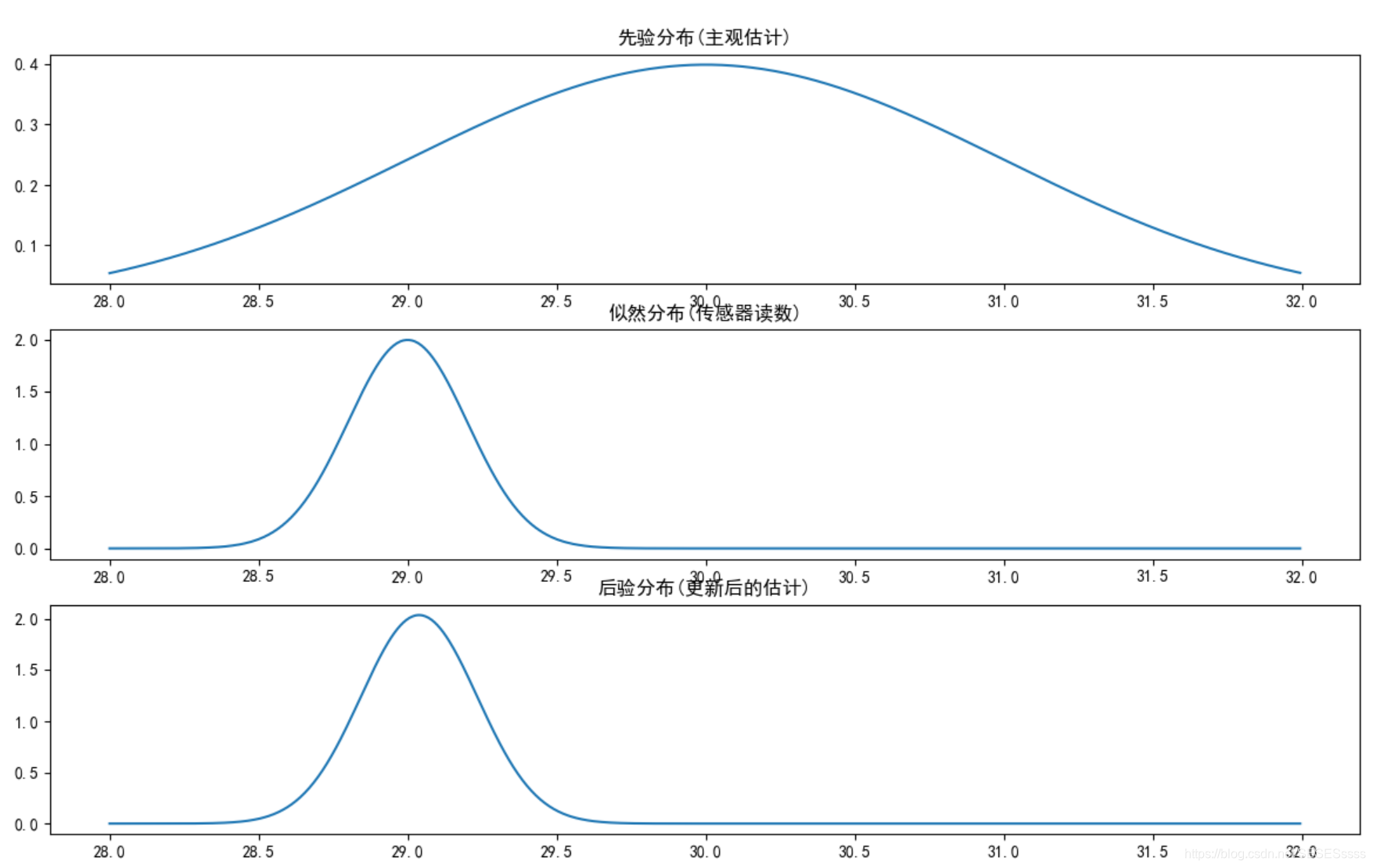
对比一下可以发现:
先验N(30,1),似然N(29,0.2^2),后验N(29.038,0.038)
方差减小了,不确定性下降了,即融合了先验与观测信息,从而实现了更精确的估计。
由于中间步骤计算繁琐,接下来直接给出推得的公式:
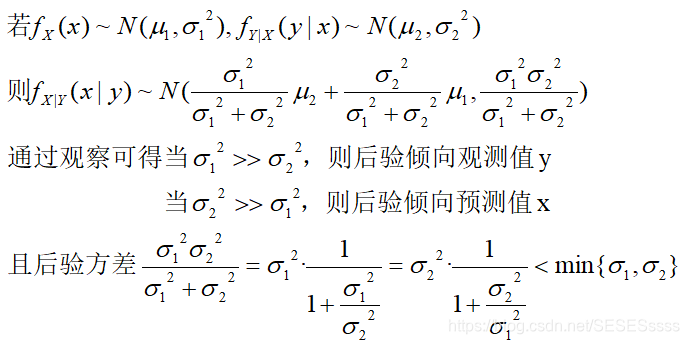
同样的,贝叶斯滤波理论也可用于多传感器融合算法(两个精度一般的传感器的运动估计->精度较高的运动估计)
随机过程的贝叶斯滤波
在前几个小节中,我们所讨论的随机变量都是相互独立的,但在机器人感知中,机器人的运动估计其实就是一个随机过程
随机过程彼此之间不独立,由一定的递推公式连接:
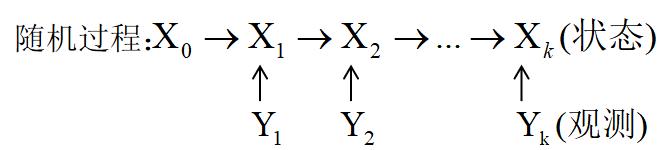
其中X_0是初值,初值一般只由主观猜测决定(先验)
那么我们如何从初始时刻的状态X_0,加上观测信息,进而估计到k时刻的状态X_k而又保证估计值的精度呢?
方法1:所有的X_0~X_k的先验概率都靠(直接忽略状态方程)
缺点:过于依赖观测值,放弃预测信息,等于说估计值的误差就是传感器的误差。
方法2:只有X_0是靠猜测,其余的X_1到X_k靠状态方程递推。
因此递推的情况下引入状态方程(预测方程):(反映X_k与X_k-1之间的关系):
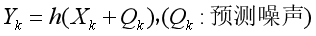
同时又有观测方程(状态与传感器读数之间的转化关系,比如状态是位移,传感器是加速度传感器,之间就有一个转换方程):
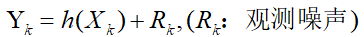
有了状态方程和观测方程,我们又该如何递推呢?
方法1:不考虑观测方程
假设有状态方程X_k=2X_k-1,无噪声(状态方程绝对准确),无观测
且初值X_0~N(0,1)则有:
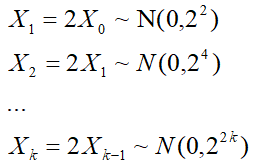
可以发现,如果只通过状态方程,由于初值X_0具有误差,因此误差会不断在迭代过程中累积,最终方差将会越来越大,模型越来越不准确。(原因:没有引入观测)
更准确的递推方式:
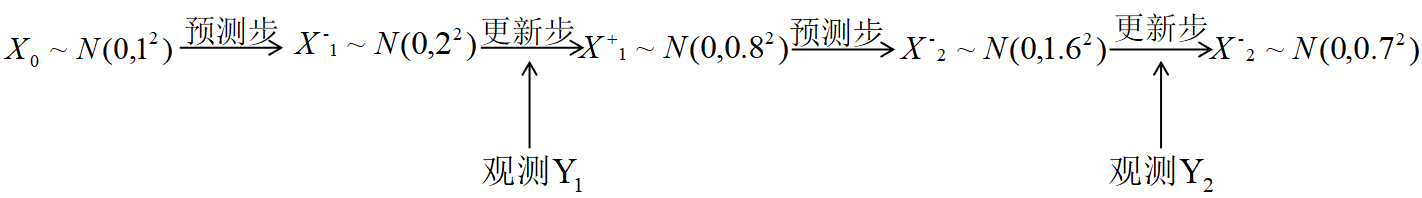
即:将上一步的后验概率作为下一步的先验概率

具体该如何实现?
详细推导过程:
已知:
1.状态方程,观测方程:
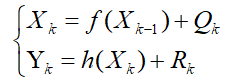
2.随机独立性
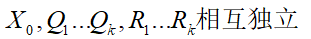
3.观测值y_1,y_2,…,y_k已知,f_0(x),f_Q_k(x),f_R_k(x)已知
重要定理:条件概率里的条件可以做逻辑推导,例:
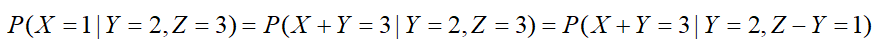
预测步:

更新步:
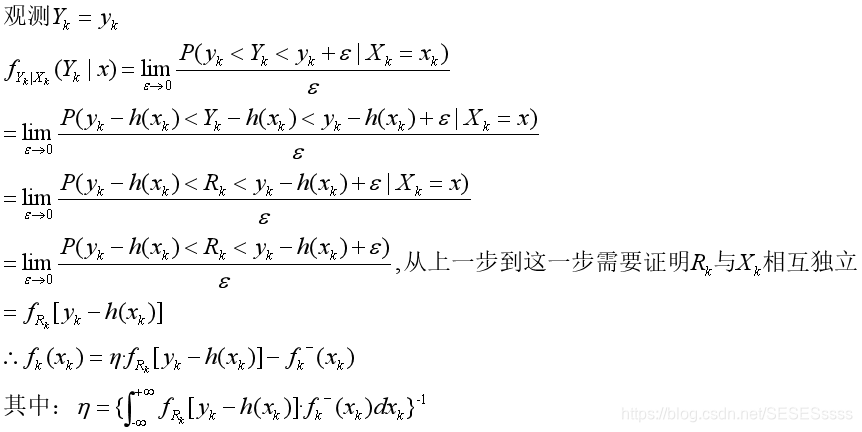
完整的递推过程:
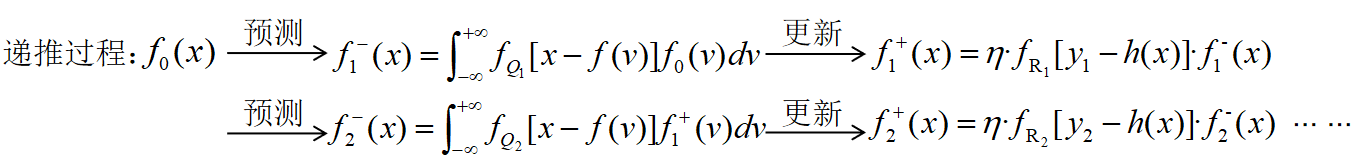
最终的贝叶斯滤波算法:

且由于状态方程可以是多变的,因此贝叶斯滤波并不能直接运用于实际算法。
因此在贝叶斯滤波理论的基础上,人们又扩展了许多算法用于解决实际问题:

参考来源:忠厚老实的王大头