给定t时刻以及之前的所有观测z和输入u,我们的目标是求得当前状态量x的概率分布(belief),即
\[bel(x_t)=p(x_t|z_{1:t}, u_{1:t})\]
在实际使用中,一般将求解过程分为两步,首先求解在t时刻观测前的先验分布,即
\[\overline{bel}(x_t)=p(x_t|z_{1:t-1}, u_{1:t})\]
然后再根据t时刻的观测通过贝叶斯公式更新先验分布,以得到后验分布,即
\[bel(x_t)=\eta p(z_t|x_t,z_{1:t-1},u_{1:t}) \overline{bel}(x_t)\]
其中\(\eta\)是归一化系数。
进一步,t时刻的先验分布可以根据全概率公式用t-1时刻的后延分布表示,即
\[ \overline{bel}(x_t)=p(x_t|z_{1:t-1}, u_{1:t}) \\ =\int{p(x_t, x_{t-1}|z_{1:t-1}, u_{1:t})}dx_{t-1} \\ =\int{p(x_t|x_{t-1},z_{1:t-1}, u_{1:t})p(x_{t-1}|z_{1:t-1}, u_{1:t})}dx_{t-1} \]
假设t-1时刻的状态与t时刻的输入无关(马尔科夫性),那么
\[ p(x_{t-1}|z_{1:t-1}, u_{1:t})=p(x_{t-1}|z_{1:t-1}, u_{1:t-1})=bel(x_{t-1}) \]
则
\[ \overline{bel}(x_t)=\int{p(x_t|x_{t-1},z_{1:t-1}, u_{1:t})bel(x_{t-1})dx_{t-1}} \]
进一步假设马尔科夫性,即t时刻的状态只和t时刻的输入以及t-1时刻的状态有关,t时刻的观测只和t时刻的状态有关,那么
\[ p(x_t|x_{t-1},z_{1:t-1}, u_{1:t})=p(x_t|x_{t-1},u_t) \\ p(z_t|x_t,z_{1:t-1},u_{1:t})=p(z_t|x_t) \]
最终可得贝叶斯滤波器的更新方程
\[ \overline{bel}(x_t)=\int{p(x_t|x_{t-1},u_t)bel(x_{t-1})dx_{t-1}} \\ bel(x_t)=\eta p(z_t|x_t)\overline{bel}(x_t) \]
一个完整的贝叶斯滤波器就是随着时间推移不断执行以上两步来完成状态量的估计。其中第一个方程称为prediction,\(p(x_t|x_{t-1},u_t)\)称为状态转移概率。第二个方程称为correction,\(p(z_t|x_t)\)称为观测概率或测量概率。
由以上推导可知,贝叶斯滤波器对系统状态的更新进行了马尔科夫假设,两个更新方程描述了一个隐马尔科夫模型(因为状态量无法直接观测到,所以为‘隐’),这也是贝叶斯滤波器与基于图的优化器的区别,基于图的优化器没有做马尔科夫假设。
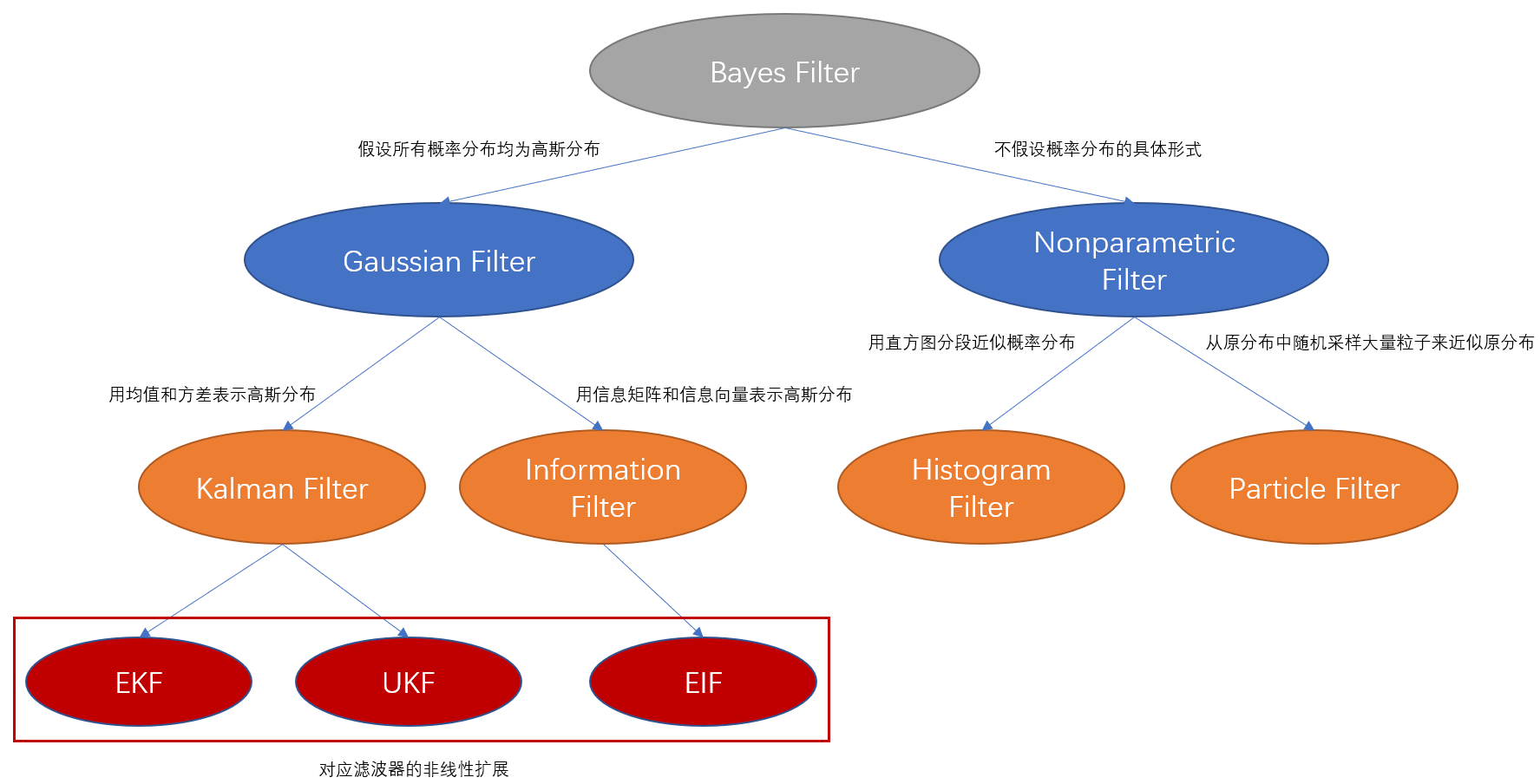
实际使用贝叶斯滤波器时,需要计算prediction步骤中的积分,离散状态量可以变为和式计算,而连续状态量则很难计算,因此对概率分布的形态进行假设或近似就得到了其他滤波器,如下图所示