朴素贝叶斯与贝叶斯网络详解

一、背景

长久以来，人们对一件事情发生或不发生的概率，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率是多少？”他们会想都不用想，会立马告诉你，取出白球的概率就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X 的变化而变化。

频率学派之所以能得出这样的结论，是因为他们研究的对象是简单可数的。比如袋子里只有黑球或者白球、一个硬币抛出只有正面和反面、一个骰子只有1-6个点。

可是现实生活中的事物并没有那么简单直观。例如，要你评估一个人的创业成功可能性。难道这时你还可以直接说50%吗？还用”要么成功要么不成功“这句话去解释吗？很显然是不合理的，因为这件事情已经不是简单可数的了。影响创业成功与否的因素有很多，例如这个人是否勤奋、是否具有创业头脑、是否拥有一定的人脉、是否可以团结周围的伙伴同事等等。这是一个连续且不可数的事件空间，

1.1 贝叶斯方法的提出

在18世纪，贝叶斯发表了一篇名为《An essay towards solving a problem in the doctrine of chances》的论文。贝叶斯学派认为事物发生的概率是随机且未知的，但是可以通过样本去预测它。用一句话概括贝叶斯方法的观点就是：任何时候，我对世界总有一个主观的先验判断，但是这个判断会随着世界的真实变化而随机修正，我对世界永远保持开放的态度。

回到上面的例子：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率θ是多少？”贝叶斯认为取得白球的概率是个不确定的值，因为其中含有机遇的成分。比如，一个朋友创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？你如果对他为人比较了解，而且有方法、思路清晰、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯式的思考方式。

贝叶斯学派认为事物发生的概率是随机且未知的，但是可以通过样本去预测它。用贝叶斯学派的理论去回答上述创业问题：假如这个人比较勤奋，那么可以推断创业成功率在80%以上，这称作 先验概率估计 。但是随着公司的运营，你发现公司的财务状况非常差，此时可以推断创业成功率由80%下降到30%，这称作 后验概率估计 。贝叶斯学派的这种动态的估计方法，就是贝叶斯方法。贝叶斯方法思考问题遵循的方式是：

先验分布 + 观测结果 => 后验分布

此处给出先验概率和后验概率的解释：

• 先验概率是 在全事件的背景下，A事件发生的概率，即 P(A|Ω)
• 后验概率是 在新事件B的背景下，A事件发生的概率，即 P(A|B)

全事件一般是统计获得的，是没有实验前的概率，所以被称为先验概率。
新事件一般是通过实验获得的，如事件B，此时事件背景从全事件变成了事件B，该事件B对A发生的概率会产生影响，所以需要对A事件的概率做出修正，即从 P(A|Ω) 变成了 P(A|B) ，所以被称为后验概率。

1.2 频率派与贝叶斯派的区别

频率派与贝叶斯派具有不同的思考方式：

• 频率派把需要推断的参数θ看做是固定的未知常数，即概率虽然是未知的，但最起码是确定的一个值。同时，样本X是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X 的分布。
• 而贝叶斯派的观点则截然相反，他们认为参数是随机变量，而样本X是固定的，由于样本是固定的，所以他们重点研究的是参数的分布。

二、分类问题

可以说，利用贝叶斯算法，就是来解决分类问题的。贝叶斯算法是分类算法的一种，这类算法都以著名的贝叶斯定理为基础。

分类器往往是根据经验方法来构造的，因为现实生活中缺少足够多的信息去构造一个100%正确率的分类器，只是在某种程度上实现一定概率意义上正确的分类器。例如，医生给病人看病就是一个典型的分类问题。任何一个医生都不可能直接看出病人患了什么病，只是通过病人的体征、描述和身体检查单给出相对正确的结果，这时医生就是一个分类器。而这个分类器的效果好坏，取决于这位医生接受的教育、病人患病症状是否明显、医生的经验是否充足等因素。

所以通俗地说，利用贝叶斯算法解决问题，首先要得到的就是分类器。还是上个例子，想要获得一个诊断病情的分类器，就需要事先喂给它足够大的样本，例如患病体征A对应疾病B的概率是多少等等这样的概率关系。当样本处理完毕之后，说白了就是概率运算，分类器也就得到了。此时代入新的病人的病情，即可获得输出。

事实上，利用贝叶斯方法解决问题，也分为不同的方式。其中最简单的就是朴素贝叶斯，即NBN(Naive Bayesian Network)。之所以称为朴素贝叶斯，是因为它的思想真的很朴素，实现起来也较为容易，可行性很强，是我们解决问题最常用的一种方法。具体内容稍后阐述。

三、基础知识

在进入贝叶斯方法之前，我们需要掌握以下基础知识，它们是贝叶斯网络的重要概念组成部分。

3.1 条件概率

又称为后验概率，就是事件A在事件B已经发生的条件上发生的概率。表示为P (A | B)，计算公式为：

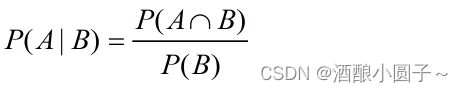
3.2 联合概率

联合概率表示两个事件共同发生的概率。A与B的联合概率表示为：

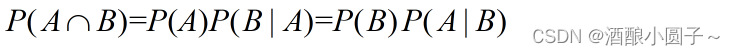
即事件A和事件B同时发生的概率为：在A发生的情况下发生B，或者在B发生的情况下发生A。

3.3 全概率公式

全概率公式将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。

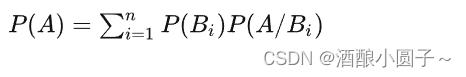
全概率公式的意义： 每一个原因都可能导致 $A$ 发生，故 $A$ 发生的概率是全部原因引起 $A$ 发生的概率的综合，即为全概率公式。

可以形象地把 全概率公式 看成是由 由原因推断结果 的公式，每个原因对结果的发生都有一定的作用，结果发生的可能性与各种原因的作用大小有关。

3.4 贝叶斯公式

在全概率公式中，如果将A看成是“结果”，Bi看成是导致结果发生的诸多“原因”之一，那么全概率公式就是一个“原因推结果”的过程。但贝叶斯公式却恰恰相反。贝叶斯公式中，我们是知道结果A已经发生了，所要做的是反过来研究造成结果发生的原因，是X原因造成的可能性有多大，即 “结果推原因” 。

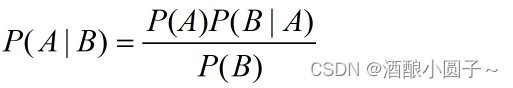
P(A|B)是在B发生的情况下A发生的可能性，其中：

• P(A)称为A的先验概率，表示事件B发生之前，我们对事件A的发生有一个基本的概率判断。
• P(A|B)称为A的后验概率：表示其事件B发生之后，我们对事件A的发生概率重新评估。
• P(B)称为B的先验概率，表示事件A发生之前，我们对事件B的发生有一个基本的概率判断。
• P(B|A)称为B的后验概率：表示事件A发生之后，我们对事件B的发生概率重新评估。

贝叶斯公式之所以有用，是因为我们在日常生活中，很容易求出P (B | A)，但是我们真正想要的是P (A | B)，往往这个P (A | B)并不是那么直观易求的。贝叶斯公式就为我们打通了这条线路。

下面展开讲解一下贝叶斯公式的推导，有兴趣的同学可以了解下：

3.4.1 推导一

贝叶斯公式可以直接根据条件概率及联合概率的定义直接推出。

因为 P(A,B) = P(A)P(B|A) = P(B)P(A|B) = P(B,A) ，所以 P(A|B) = P(A)P(B|A) / P(B)。

更为规范化的推导过程如下：

3.4.2 推导二

参考博客：全概率公式、贝叶斯公式：https://zhuanlan.zhihu.com/p/78297343

贝叶斯公式的推导：由条件概率出发，分子通过一步条件概率变形，分母通过全概率公式变形。重点：不必分子分母同时变形，只变其中之一也行。所以就有了下面公式：

可以形象地把 贝叶斯公式 看成是由 由结果推断原因 的公式，在事件发生的条件下，考察每种情况出现的条件概率。

四、朴素贝叶斯

朴素贝叶斯分类是一种非常简单的分类方法，它最突出的特点就是：假设分类项的的各个特征之间是相互独立的！

正是因为这个特点，才使得整个朴素贝叶斯的可操作性很高，并且思想简单易懂。

朴素贝叶斯的思想就是：对于给出的待分类项，求解在此分类项的条件下，各个类别哪个出现的概率最大，取概率最大的那个类别为该待分类项的类别。

通俗来说，就好比这么个道理：你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

4.1 贝叶斯定理用于分类

贝叶斯定理：给定x为样本，c为该样本所对应的分类，根据贝叶斯公式，我们可以得到：

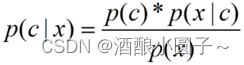
其中：

• p(c )为类先验概率，即各类样本所占的比例。可以基于训练数据集D来估计得到。
• p(x)是用于归一化的证据因子(evidence),对于给定样本x，p(x)与类标记无关。
• p(x|c)为样本x相对于类标记c的类条件概率(似然)。涉及x所有属性的联合概率，难以从有限样本中估计。

因此，求解p(c|x)的问题的关键在于：如何基于训练数据D来估计先验p(c )和条件概率p(x|c) （ 主要是如何求p(x|c) ）。

对于求解条件概率p(x|c)，常规的做法是使用极大似然估计，通过采样来估计概率分布参数，从而求解p(x|c)。

4.2 朴素贝叶斯分类器

为了避开求解类条件概率 p(x|c) 的障碍（需求出所有属性上的联合概率），朴素贝叶斯采用了属性条件独立性假设 ：即对于已知类别，假设所有属性相互独立，即每个属性独立地对分类结果产生影响，则：

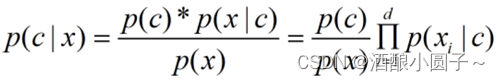
其中d为属性数目，xi为x在第i个属性上的取值。
注意，这里只有基于属性条件独立性假设，才能归纳为上述公式。

由于对所有类别而言p(x)相同，因此可得朴素贝叶斯分类器的表达式：

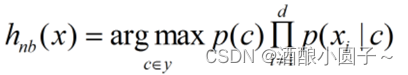
朴素贝叶斯分类器的训练过程即：基于训练集D估计先验概率p©，并为每个属性估计条件概率p(xi|c)。具体步骤如下：

(1) 计算先验概率p(c )

令Dc表示训练集D中第c类样本组成的集合。N为D中可能的类别数。

(2) 计算条件概率p(xi|c)

• 离散属性
  令Dc,xi表示Dc在第i个属性上取值为xi的样本组成的集合。Ni为属性Xi可能的取值个数。

• 连续属性。当特征属性为连续值时，通常假定其值服从高斯分布（也称正态分布）。即：

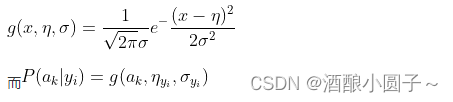
因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差，代入上述公式即可得到需要的估计值。均值与标准差的计算在此不再赘述。

(3) Laplace修正

当某个类别下某个特征划分没有出现时，会有P(xi|c)=0，就是导致分类器质量降低，所以此时引入Laplace修正，就是对每类别下所有属性(划分)的计数加1。

4.3 朴素贝叶斯计算过程

回到我们之前按肤色、身高、外形等特征推测路人属于亚洲人、美洲人、非洲人概率的样例，计算过程如下：

根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：

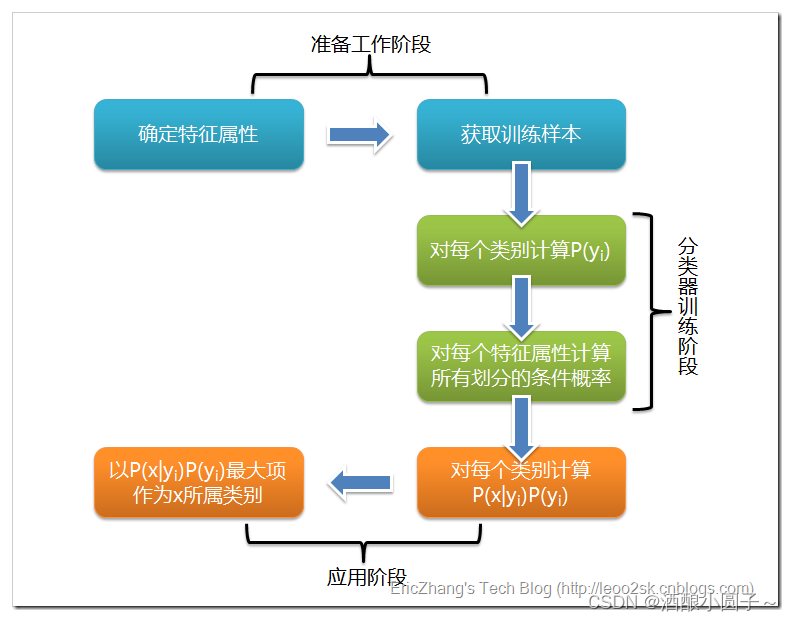
根据上述朴素贝叶斯的定义，可以看出朴素贝叶斯分类大致分为三个阶段：

• 第一阶段——准备工作阶段：确定待分类项的所属集合，例如{亚洲人，美洲人，非洲人}，接着确定特征属性，例如{肤色，身高，眼睛颜色}，与此同时要对这些特征属性进行划分，例如什么样的人种对应什么样的眼睛颜色。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是唯一需要人工处理的阶段，其质量对于整个过程有着重要的影响，因为接下来分类器的质量很大程度上取决于特征属性、特征属性的划分和训练样本的质量。

• 第二阶段——分类器训练阶段：这个阶段就是生成分类器。主要工作就是计算每个类别在训练样本中的出现频率和在每个类别的条件上特征属性出现的概率。这一阶段的输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，可以由程序自动完成。

• 第三阶段——应用阶段：这个阶段就是利用分类器对待分类项进行分类，输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，可由程序自动完成。

4.4 朴素贝叶斯分类实例

下面举出一个用朴素贝叶斯解决实际问题的例子——检测SNS社区中的真实账号。

对于SNS(Social Networking Services)社区来说，虚假账号的存在是一个普遍性问题，作为SNS社区的运营商，他们希望检测出这些虚假账号，从而在一些运营分析报告中避免这些账号的干扰，从而加强对SNS社区的了解和监督。

如果采用人工检测，那么难度可想而知，如果可以引入自动检测机制，必将大大提升工作效率。这个问题说白了，就是对社区中的账号进行分类，是真实账号还是虚假账号，下面我们一步步实现这个过程。

首先设 $C=0$ 表示真实账号， $C=1$ 表示虚假账号。

第一步——确定特征属性及其划分：
这一步我们要找出能够区分真实账号和虚假账号的特征属性。在实际的应用中，特征属性的数量肯定是很多的，此处仅采用少量的特征属性进行说明。

我们选择三个特征属性：

• a1 :日志数量/注册天数，
• a2 :好友数量/注册天数，
• a3：是否使用真实头像。

在SNS社区中，这三个特征属性都是可以直接从数据库中算出来的。

下面给出这三个特征属性的划分：
a1 : {a <= 0.05，0.05 < a < 0.2，a >= 0.2}，
a2 : {a <= 0.1，0.1 < a < 0.8，a >= 0.8}，
a3 : {a = 0(未采用)，a = 1(采用)}

第二步——获取训练样本：

这里使用运维人员曾经人工检测过的1万个账号作为训练样本。

第三步——计算训练样本中每个类别的频率：

假设训练样本中共有10000个社交账号，真实账号有8900个，虚假账号有1100个，则有：

$P(C=0)=0.89$
$P(C=1)=0.11$

第四步——计算每个类别条件下各个特征属性划分的条件概率：

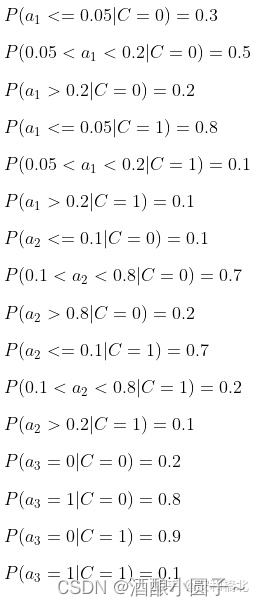
第五步——使用分类器进行鉴别：

4.5 朴素贝叶斯的缺点

在用朴素贝叶斯去解决SNS社区虚假账号问题的解决方案中，我们做出了如下假设：

• 真实账号比非真实账号平均具有更大的日志密度、更大的好友密度、更多地使用真实头像。
• 日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的，也就是特征属性之间的独立性。

但是第二条假设很有可能不成立，因为好友密度除了与账号真实性相关之外，还和是否使用真实头像有关。当你使用真实头像的时候，肯定是趋向于吸引更多的人加你为好友，从而拥有更大的好友密度。

朴素贝叶斯的缺点在于：朴素贝叶斯假设特征之间独立，但是实际上，特征之间往往是不独立的。

在特征之间不独立的情况下，虽然我们为了简化问题，可以假设特征之间独立，然后使用贝叶斯网络来解决问题，但是可能存在分类效果不佳的问题。
这时，可以考虑使用有向无环图DAG来进行概率图的描述，并结合贝叶斯网络实现分类。

五、贝叶斯网络

5.1 贝叶斯网络介绍

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型。

贝叶斯网络中的节点表示随机变量，有向边表示变量之间有因果关系(非条件独立)，两个用箭头连接的节点就会产生一个条件概率值，如下图所示：

设 $G=(I,E)$ 表示一个DAG，其中 $I$是图形中所有节点的集合， $E$ 是所有有向边的集合，函数 $pa(x)$ 表示从子节点x到父节点的映射。令 $x_i$ 表示DAG中某一节点i代表的随机变量，则概率 $p(x_i)$ 可以表示成：

则称此DAG为贝叶斯网络模型。

注意，贝叶斯网络有一个极为重要的性质：每一个节点在其直接前驱节点（父节点）的值制定后，这个节点条件独立于其所有非直接前驱前辈节点。

这条特性的重要意义在于明确了贝叶斯网络可以方便计算联合概率分布。一般情况下，多变量非独立联合条件概率分布有如下求取公式：

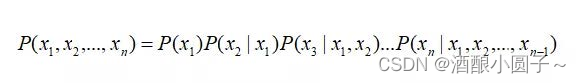
当有了上述性质之后，该式子就可以简化为：

基于先验概率、条件概率分布和贝叶斯公式，我们便可以基于贝叶斯网络进行概率推断。

许多经典的多元概率模型都是贝叶斯网络的特例，例如朴素贝叶斯模型、马尔科夫链、隐马尔科夫模型、卡尔曼滤波器、条件随机场等等。

5.2 贝叶斯网络的基本结构

三节点对应的三角结构是贝叶斯网络信息流动的最基本结构，下面介绍4种经典的信息流动结构。

5.2.1 head-to-head（共同作用）

根据上图以及链式法则，有P(a,b,c) = P(a) * P(b) * P(c|a,b)成立，因为P(c|a,b) = P(a,b,c)/P(a,b)，将P(a,b,c)消除，从而得到P(a,b) = P(a)*P(b)。

因为我们可以得到：

• 当c未知时，a和b是被阻隔的，是独立的，称之为head-to-head条件独立。
• 当c已知时，a和b不独立，a的信息可以沿着c流向b。

我们可以形象地理解为，将abc想象成河流，两条小河（a、b）流入一条大河（c），当c是未知时，a-> c <-b之间的流动是阻断的，那么影响将无法沿着“a-> c <-b”流动。形如“a-> c <-b”的这种结构也称为一个v-结构（v-structure）。

5.2.2 tail-to-tail（共同原因）

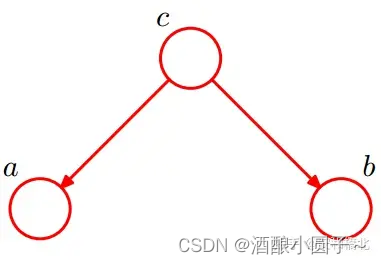
同样的，根据上图和链式法则，我们可以得到：P(a,b,c) = P© * P(a|c) * P(b|c)。

• 当c未知时，我们没办法通过上式得到P(a,b) = P(a) * P(b)。因此c未知时，a、b不独立，a可以通过c影响b。
• 当c已知时，有P(a,b|c) = P(a,b,c) / P©，将上式的P(a,b,c)代入进来，就可以得到P(a,b|c) = P(a|c) * P(b|c)，从而得到a和b在此条件下是独立的。因此当c已知时，a和b被阻断，a和b是独立的。

我们可以形象地理解为，一条大河流到c节点的时候要分成两条支流，当c给定的时候，即c节点放开，此时a和b就是两条互不影响的支流，因此是相互独立的。

5.2.3 head-to-tail（因果迹）

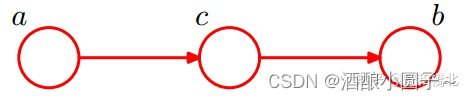
同样的，根据上图和链式法则，我们可以得到：P(a,b,c) = P(a) * P(c|a) * P(b|c)。

• 当c未知时，我们没办法通过上式得到P(a,b) = P(a)*P(b)。因此c未知时，a、b不独立，a可以通过c影响b。
• 当c已知时，有P(a,b|c) = P(a,b,c) / P(c ) 和 P(a,c) = P(a) * P(c|a)，将这两式代入上述式子，即可得到P(a,b|c) = P(a|c) * P(b|c)，从而得到a和b在此条件下是独立的。因此当c已知时，a和b被阻断，a和b是独立的。

5.2.4 tail-to-head（证据迹）

同样的，根据上图和链式法则，我们可以得到：P(a,b,c) = P(b) * P(c|b) * P(a|c)。

• 当c未知时，我们没办法通过上式得到P(a,b) = P(a)*P(b)。因此c未知时，a、b不独立，a可以通过c影响b。
• 当c已知时，有P(a,b|c) = P(a,b,c) / P(c ) 和 P(b,c) = P(b) * P(c|b)，将这两式代入上述式子，即可得到P(a,b|c) = P(a|c) * P(b|c)，从而得到a和b在此条件下是独立的。因此当c已知时，a和b被阻断，a和b是独立的。

5.3 贝叶斯网络的学习及推断

5.3.1 贝叶斯网络的学习

若网络结构已知，即属性间的依赖关系已知，则贝叶斯网络的学习过程相对简单，只需要通过对训练数据计数，估计出每个节点的条件概率表即可。但在现实应用中，我们往往并不知道网络结构。于是，贝叶斯网络的首要任务就是根据训练数据集来找出结构最为恰当的贝叶斯网。“评分搜索”是求解这一问题的常用办法。这里我们不再展开讲解，感兴趣的同学可以自行翻阅周志华老师的西瓜书查看。

5.3.2 贝叶斯网络的推断

先来看几个简单的贝叶斯网络：

（1）最简单的贝叶斯网络

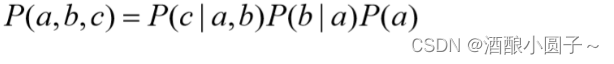
（2）较为复杂的贝叶斯网络

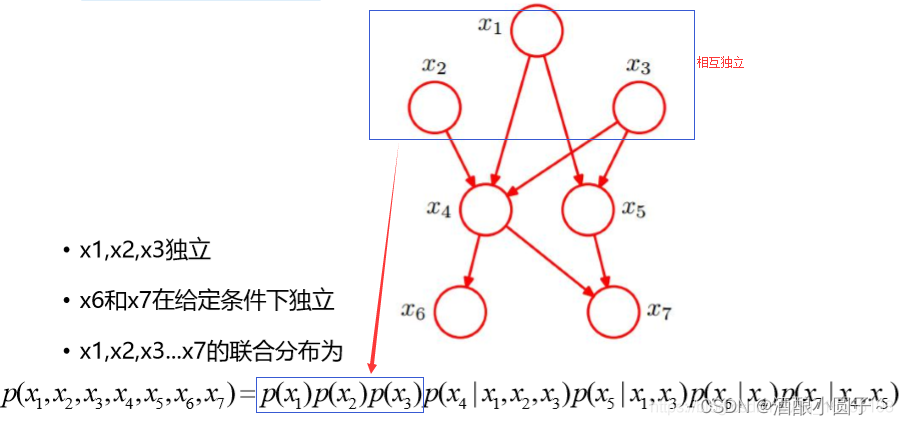
5.3.2.1 近似推断——吉布斯采样

基于已知机构的贝叶斯网络，通过一些属性变量的观测值来推断其他属性变量的取值称为贝叶斯网络的推断。最为理想的方式是直接根据贝叶斯网络定义的联合概率分布来计算后验概率。但是，这样的“精确推断”被证明是NP难的——即当网络节点较多，连接稠密时，难以进行精确推断，此时需要借助“近似推断”。

贝叶斯网的近似推断常使用吉布斯采样（Gibbs sampling）来完成。关于吉布斯采样这里不再展开讲解。

5.3.2.2 存在隐变量——EM算法

在前面的讨论中，我们一直假设训练样本中所有属性变量的值都已经被观测到，即训练样本是“完整的”。但是在现实应用中往往会遇到“不完整”的训练样本。比如，存在某个属性变量未知的情况，这种情形下，我们可以使用EM（Expectation-Maximum, EM）算法来对模型的参数进行估计。

EM算法是常用的估计隐变量的利器，它是一种迭代式的方法，其基本想法是：

• 若参数θ已知，则可根据训练数据推断出最优隐变量Z的值（E-Step）
• 若隐变量Z的值已知，则可以方便地对参数θ做极大似然估计（M-Step）

直到收敛到局部最优解。

事实上，隐变量估计问题也可以通过梯度下降等优化算法求解，但由于求和的项数将随着隐变量的数目以指数级上升，会给梯度计算带来麻烦。而EM算法则可以看作是一种非梯度优化方法。

5.4 贝叶斯网络的应用示例

回到检测SNS社区虚假账号问题，为了获得更准确的分类，我们采用如下假设：

• 真实账号比非真实账号平均具有更大的日志密度、更大的好友密度、更多地使用真实头像。
• 日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的，也就是特征属性之间的独立性。
• 使用真实头像的用户相比使用虚假头像的用户具有更大的好友密度。

上述的假设更符合真实情况，但是也伴随着一定的问题，那就是特征属性之间不再是相互独立的了，而是存在了依赖关系，使得朴素贝叶斯不再适用了。下图表示各个特征属性之间的关联：

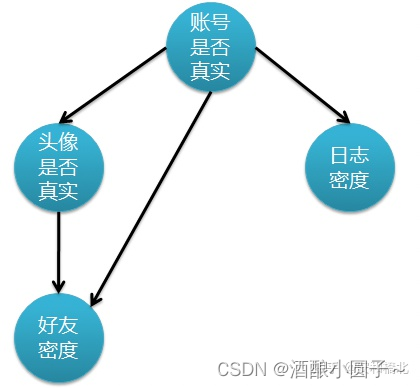
上图是一个DAG有向无环图，每个节点代表一个随机变量，每条有向边代表随机变量之前的关系。

5.4.1 构造和训练步骤

不过仅有这个贝叶斯网络图，只能反映定性关系。要想反映定量关系，还需要通过对训练数据集进行统计。假设通过人工统计，我们得到了下表(R表示账号真实性，H表示头像真实性)：

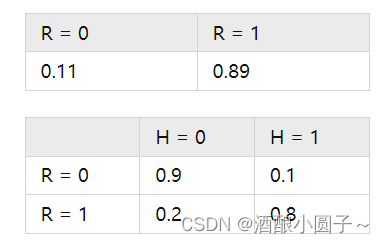
纵向表头表示条件变量，横向表头表示随机变量。上表为真实账号和非真实账号的概率，而下表为头像真实性对于账号真实性的概率。这两张表分别为“账号是否真实”和“头像是否真实”的条件概率表。

有了这些数据，不但能顺向推断，还能通过贝叶斯定理进行逆向推断。例如，现随机抽取一个账户，已知其头像为假，求其账号也为假的概率：

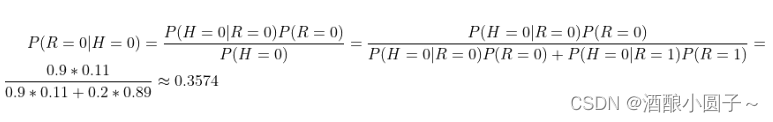
也就是说，在仅知道头像为假的情况下，有大约35.7%的概率此账户也为假。

由此我们可以看出，构造和训练贝叶斯网络分为以下两步：

• 确定随机变量间的拓扑关系，形成DAG。这一步通常需要领域专家完成，而想要建立一个好的拓扑结构，通常需要不断迭代和改进才可以。
• 训练贝叶斯网络。这一步也就是要完成条件概率表的构造。如果每个随机变量的值都是可以直接观察的，像我们上面的例子比较简单，那么这一步的训练是直观的，方法类似于朴素贝叶斯分类。（但是通常贝叶斯网络的中存在隐藏变量节点，那么训练方法就比较复杂，例如使用梯度下降法或者EM算法进行优化。详见本文 5.3.2.2 小节。）

5.4.2 推理过程

就使用方法来说，贝叶斯网络主要用于概率推理及决策，具体来说，就是在信息不完备的情况下通过可以观察随机变量推断不可观察的随机变量，并且不可观察随机变量可以多于以一个，一般初期将不可观察变量置为随机值，然后进行概率推理。下面举一个例子：

还是SNS社区中不真实账号检测的例子，我们的模型中存在四个随机变量：账号真实性R，头像真实性H，日志密度L，好友密度F。其中H，L，F是可以观察到的值，而我们最关系的R是无法直接观察的。这个问题就划归为通过H，L，F的观察值对R进行概率推理。

推理过程可以如下所示：

• 使用观察值实例化H,L和F，把随机值赋给R。
• 计算 P(R|H, L, F) = P(H|R)P(L|R)P((F|R,H)，其中相应的概率值查询上述构造的条件概率表。（这里，头像真实性H是好友密度F的parent）

由于上述例子只有一个未知随机变量，所以不用迭代。

更一般的，还需要使用迭代法利用贝叶斯网络进行推理。具体步骤如下：
1、对所有可观察随机变量节点用观察值实例化；对不可观察节点实例化为随机值。
2、对DAG进行遍历，对每一个不可观察节点y，计算

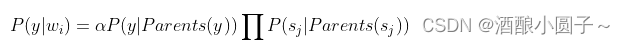
其中wi表示除y以外的其它所有节点，a为正规化因子，sj表示y的第j个子节点。
3、使用第三步计算出的各个y作为未知节点的新值进行实例化，重复第二步，直到结果充分收敛。
4、将收敛结果作为推断值。

以上只是贝叶斯网络推理的算法之一，另外还有其它算法，这里不再详述。

参考资料

• 贝叶斯网络 Bayesian Network：https://zhuanlan.zhihu.com/p/542482587
• 算法杂货铺——分类算法之贝叶斯网络(Bayesian networks) ：https://www.cnblogs.com/leoo2sk/archive/2010/09/18/bayes-network.html