支持向量机（Support Vector Machines，SVM）

文章目录

1. 线性可分SVM 与硬间隔最大化

1.1 线性可分SVM
1.2 函数间隔、几何间隔
1.3 间隔最大化

2. 线性SVM 与软间隔最大化

2.1 线性SVM

3. 非线性SVM 与核函数

3.1 核技巧/核函数
3.2 常用核函数
3.3 非线性SVM分类

4. 序列最小最优化算法
5. sklearn SVC 实例
6. 课后习题

支持向量机（SVM）是一种二类分类模型。
支持向量机还包括核技巧，实质上是非线性分类器。
学习策略：间隔最大化
学习算法：求解凸二次规划的最优化算法。
当训练数据线性可分时，通过硬间隔最大化（hard margin maximization），学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机
当训练数据近似线性可分时，通过软间隔最大化（soft margin maximization），也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机
当训练数据线性不可分时，通过使用核技巧（kernel trick）及软间隔最大化，学习非线性支持向量机
核函数（kernel function）表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。通过使用核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机

1. 线性可分SVM 与硬间隔最大化

1.1 线性可分SVM

输入都由输入空间转换到特征空间，支持向量机的学习是在特征空间进行的。

假设数据集线性可分
找到分离超平面将数据分为 +1，-1类
感知机利用误分类最小的策略，求得分离超平面，有无穷多个
线性可分SVM 利用间隔最大化求最优分离超平面，解是唯一的

1.2 函数间隔、几何间隔

超平面 $(\omega,b)$ 关于样本 $(x_i,y_i)$ 的函数间隔：
$\hat \gamma_i = y_i(\omega \bullet x_i +b)$
超平面 $(\omega,b)$ 关于数据集 $T$ 的函数间隔：对所有点，取 $\min$
$\hat \gamma = \min\limits_{i=1,...,N}\hat \gamma_i$

超平面 $(\omega,b)$ 关于样本 $(x_i,y_i)$ 的几何间隔：
$\gamma_i = y_i\bigg(\frac{\omega}{||\omega||_2} \bullet x_i +\frac{b}{||\omega||_2}\bigg)$
超平面 $(\omega,b)$ 关于数据集 $T$ 的几何间隔：对所有点，取 $\min$
$\gamma = \min\limits_{i=1,...,N}\gamma_i$

函数间隔、几何间隔的关系

$\gamma_i = \frac{\hat \gamma_i}{||\omega||_2},\quad \gamma = \frac{\hat \gamma}{||\omega||_2}$

如果 $||\omega||_2 = 1$ ，那么函数间隔和几何间隔相等。
如果超平面参数 w 和 b 成比例地改变（超平面没有改变），函数间隔也按此比例改变，而几何间隔不变。

1.3 间隔最大化

SVM学习的基本想法：能够正确划分，且几何间隔最大的分离超平面

几何间隔 最大的分离超平面是唯一的。
这里的间隔最大化又称为硬间隔最大化（与训练数据集近似线性可分时的软间隔最大化相对应）
间隔最大化的直观解释是：以充分大的确信度对训练数据进行分类。这样的超平面应该对未知的新实例有很好的分类预测能力

线性可分SVM学习最优化问题：
$\color{red}\min _{w, b} \quad \frac{1}{2}\|w\|^{2} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad$

$\color{red}s.t. \quad y_{i}\left(w \bullet x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N$

求得最优化问题的解为 $w^*$ ， $b^*$ ，得到线性可分支持向量机，分离超平面是

$w^{*} \bullet x+b^{*}=0$

分类决策函数是

$f(x)=\operatorname{sign}\left(w^{*} \bullet x+b^{*}\right)$

支持向量、间隔边界
在线性可分情况下，样本点中与分离超平面距离最近的样本点的实例称为支持向量（support vector）
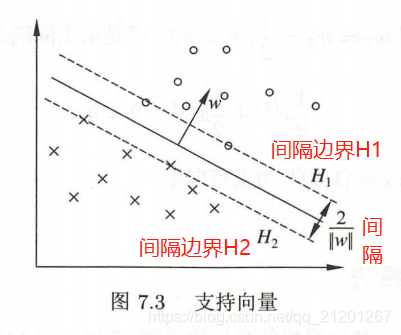
决定分离超平面时只有支持向量起作用，而其他实例点并不起作用
移动支持向量将改变所求的解；在间隔边界以外移动其他实例点，甚至去掉这些点，解不变
支持向量在确定分离超平面中起着决定性作用，支持向量的个数一般很少，所以SVM由很少的“重要的”训练样本确定

对偶问题：
$\color{red} \min\limits_\alpha \quad \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \bullet x_{j}\right)-\sum_{i=1}^{N} \alpha_{i}$

$\color{red} s.t. \quad \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad$

$\color{red} \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \quad \quad$

通常，通过求解对偶问题学习线性可分支持向量机，即首先求解对偶问题的最优值

$a^*$ ，然后求最优值 $w^*$ 和 $b^*$ ，得出分离超平面和分类决策函数。

$\omega^* = \sum\limits_{i=1}^N \alpha_i^*y_ix_i, \quad b^* =y_i-\sum\limits_{i=1}^N \alpha_i^*y_i(x_i \bullet x_j)$

分离超平面是

$w^{*} \bullet x+b^{*}=0 \quad \Rightarrow \quad \sum\limits_{i=1}^N \alpha_i^*y_i(x \bullet x_i)+b^*=0$

分类决策函数是

$f(x)=\operatorname{sign}\left(w^{*} \bullet x+b^{*}\right) \quad \Rightarrow \quad f(x)=\operatorname{sign}\left(\sum\limits_{i=1}^N \alpha_i^*y_i(x \bullet x_i)+b^*\right)$

$\color{red}\alpha_i^* > 0$ 的样本点称为支持向量，其一定在间隔边界上。

2. 线性SVM 与软间隔最大化

2.1 线性SVM

线性可分SVM学习方法，对线性不可分训练数据是不适用的，怎么将它扩展到线性不可分，需要修改硬间隔最大化，使其成为软间隔最大化。

引入松弛变量 $\xi_{\mathrm{i}}$ ， $C>0$ 是惩罚参数，线性SVM学习的凸二次规划问题，

原始最优化问题：

$\color{red}\min _{w, b, \xi} \quad \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad$

$\color{red} s.t. \quad y_{i}\left(w \bullet x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N$

$\color{red} \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N \quad \quad \quad \quad$

求解原始最优化问题的解 $w^*$ 和 $b^*$ ，得到线性SVM，其分离超平面为

$w^{*} \bullet x+b^{*}=0$

分类决策函数是

$f(x)=\operatorname{sign}\left(w^{*} \bullet x+b^{*}\right)$

线性不可分支持向量机的解 $w^*$ 唯一，但 $b^*$ 不唯一。

对偶问题：

$\color{red} \min _{\alpha} \quad \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \bullet x_{j}\right)-\sum_{i=1}^{N} \alpha_{i}$

$\color{red} s.t. \quad \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad$

$\color{red} 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N$

线性支持向量机的对偶学习算法，首先求解对偶问题得到最优解 $\alpha^*$ ，然后求原始问题最优解 $w^*$ 和 $b^*$ ，得出分离超平面和分类决策函数。

$\omega^* = \sum\limits_{i=1}^N \alpha_i^*y_ix_i, \quad b^* =y_i-\sum\limits_{i=1}^N \alpha_i^*y_i(x_i \bullet x_j)$

分离超平面是

$w^{*} \bullet x+b^{*}=0 \quad \Rightarrow \quad \sum\limits_{i=1}^N \alpha_i^*y_i(x \bullet x_i)+b^*=0$

分类决策函数是

$f(x)=\operatorname{sign}\left(w^{*} \bullet x+b^{*}\right) \quad \Rightarrow \quad f(x)=\operatorname{sign}\left(\sum\limits_{i=1}^N \alpha_i^*y_i(x \bullet x_i)+b^*\right)$

对偶问题的解 $\alpha^*$ 中满足 $\color{red}\alpha_i^{*}>0$ 的实例点 $x_i$ 称为(软间隔)支持向量。
支持向量可在间隔边界上，也可在间隔边界与分离超平面之间，或者在分离超平面误分一侧。最优分离超平面由支持向量完全决定。
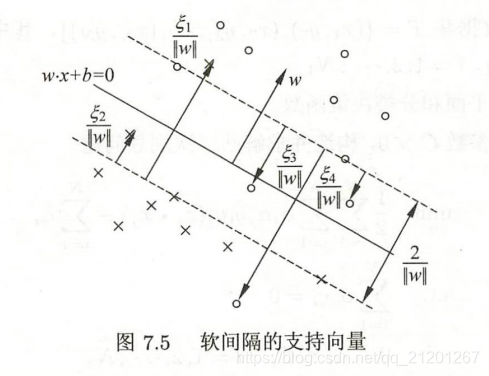
在这里插入图片描述
线性SVM学习等价于 最小化二阶范数正则化的合页函数

$\min _{w, b} \quad \sum_{i=1}^{N}\left[1-y_{i}\left(w \bullet x_{i}+b\right)\right]_{+}+\lambda\|w\|^{2}$

在这里插入图片描述
合页损失函数不仅要正确分类，而且确信度足够高时损失才是0。也就是说，合页损失函数对学习有更高的要求

3. 非线性SVM 与核函数

核技巧（kernel trick）不仅应用于支持向量机，而且应用于其他统计学习问题。

3.1 核技巧/核函数

在这里插入图片描述
用线性分类求解非线性分类问题分为两步：

使用一个变换将原空间的数据映射到新空间
在新空间里用线性分类学习方法从训练数据中学习分类模型

用核函数来替换前面式子中的内积。
核函数表示，通过一个非线性转换后的两个实例间的内积。具体地， $K(x,z)$ 是一个核函数，或正定核，意味着存在一个从输入空间 x 到特征空间的映射 $\mathcal{X} \rightarrow \mathcal{H}$ ，对任意 $\mathcal{X}$ ，有

$K(x, z)=\phi(x) \cdot \phi(z)$

对称函数 $K(x,z)$ 为正定核的充要条件：

对任意 $\mathrm{x}_{\mathrm{i}} \in \mathcal{X}, \quad \mathrm{i}=1,2, \ldots, \mathrm{m}$ ，任意正整数 $m$ ，对称函数 $K(x,z)$ 对应的 Gram 矩阵是半正定的。

线性支持向量机学习的对偶问题中，用核函数 $K(x,z)$ 替代内积，求解得到的就是非线性SVM
$\color{red} f(x)=\operatorname{sign} \Bigg(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} K(x, x_i)+b^*\Bigg)$

3.2 常用核函数

对于任意函数，验证其对任意输入集，验证 K 对应的 Gram 矩阵是否是半正定的，很困难，所以用已有的核函数。

多项式核函数
$K(x,z) = (x \bullet z + 1)^p$
高斯核函数
$K(x,z) = \exp \bigg(- \frac{||x-z||^2}{2 \sigma^2} \bigg)$
字符串核函数（离散空间）

3.3 非线性SVM分类

选取适当的核函数 $K(x,z)$ , 适当的参数 $C$ , 构造最优化问题：
$\color{red} \min _{\alpha} \quad \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K \left(x_{i} ,x_{j}\right)-\sum_{i=1}^{N} \alpha_{i}$

$\color{red} s.t. \quad \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad$

$\color{red} 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N$

求解对偶问题得到最优解 $\alpha^*$ ，选择 $\alpha^*$ 的一个正分量 $0<\alpha_j^* < C$ ,计算

$\color{red} b^* =y_i-\sum\limits_{i=1}^N \alpha_i^*y_i K \left(x_{i} ,x_{j}\right)$

分类决策函数是

$\color{red} f(x)=\operatorname{sign}\left(\sum\limits_{i=1}^N \alpha_i^*y_i K \left(x ,x_{i}\right)+b^*\right)$
当 $K(x,z)$ 是正定核函数时，上面问题是凸二次规划问题，解存在。

4. 序列最小最优化算法

SMO（sequential minimal optimization）算法是SVM学习的一种快速算法

特点：不断地将原二次规划问题分解为只有两个变量的二次规划子问题，并对子问题进行解析求解，直到所有变量满足KKT条件为止。

这样通过启发式的方法得到原二次规划问题的最优解。因为子问题有解析解，所以每次计算子问题都很快，虽然计算子问题次数很多，但在总体上还是高效的。

5. sklearn SVC 实例

官方文档：sklearn.svm.SVC

class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0,
shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None,
verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, 
random_state=None)

参数：

- C：正则化参数C，默认值是1.0

C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，
      趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。
C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

- kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ 
    
    – 线性：u'v
    – 多项式：(gamma*u'*v + coef0)^degree
    – RBF函数：exp(-gamma|u-v|^2)
    – sigmoid：tanh(gamma*u'*v + coef0)

- degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

- gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。

- coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

- probability ：是否采用概率估计？ 默认为False

- shrinking ：是否采用shrinking heuristic方法，默认为true

- tol ：停止训练的误差值大小，默认为1e-3

- cache_size ：核函数cache缓存大小，默认为200

- class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

- verbose ：允许冗余输出？

- max_iter ：最大迭代次数。-1为无限制。

- decision_function_shape ：‘ovo’, ‘ovr’, default=‘ovr’

- random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。

# -*- coding:utf-8 -*-
# @Python Version: 3.7
# @Time: 2020/3/20 14:23
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: 7.SupportVectorMachine.py
# @Reference: https://github.com/fengdu78/lihang-code

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVC


def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if (data[i, -1] == 0):
            data[i, -1] = -1
    return data[:, :2], data[:, -1]


X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
clf = SVC()
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))

6. 课后习题

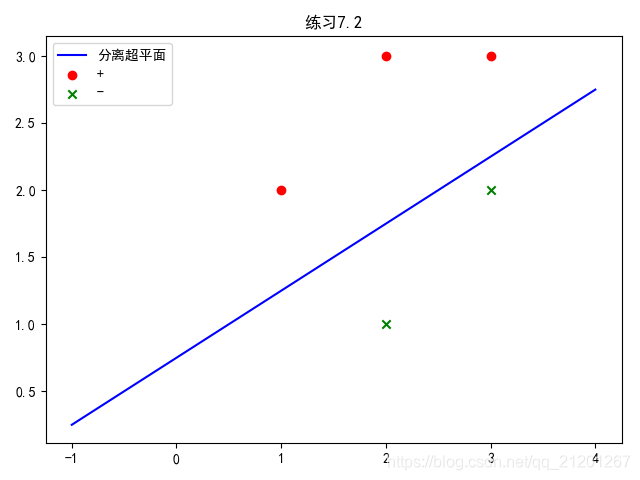
习题7.2：已知正例点 $x_1=(1,2)^T,x_2=(2,3)^T,x_3=(3,3)^T$ ，负例点 $x_4=(2,1)^T,x_5=(3,2)^T$ ，试求最大间隔分离超平面和分类决策函数，并在图上画出分离超平面、间隔边界及支持向量。

解：
在这里插入图片描述

import numpy
m = 10000;
a = []
for a1 in numpy.linspace(0,3,30):
    for a2 in numpy.linspace(0,3,30):
        for a3 in numpy.linspace(0,3,30):
            for a4 in numpy.linspace(0,3,30):
                if a1+a2+a3-a4 >= 0:
                    ans = 2*a1**2+a2**2+0.5*a3**2+a4**2+2*a1*a2-2*a1*a4+a2*a3+a3*a4-2*a1-2*a2-2*a3
                    if  ans < m:
                        a = [a1, a2, a3, a4, a1+a2+a3-a4]
                        m = ans
print(m,a)
a5 = a[0]+a[1]+a[2]-a[3]
w1 = 1*a1+2*a2+3*a3-2*a4-3*a5
w2 = 2*a1+3*a2+3*a3-1*a4-2*a5
print(w1,w2)

-2.4988109393579077 [0.5172413793103449, 0.0, 1.9655172413793103, 0.0, 2.4827586206896552]
4.551724137931034 16.03448275862069

跟下面结果不一致，有点问题

编程解 7.2 习题

# -*- coding:utf-8 -*-
# @Python Version: 3.7
# @Time: 2020/3/20 14:23
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: 7.SupportVectorMachine.py
# @Reference: https://github.com/fengdu78/lihang-code

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.svm import SVC


def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if (data[i, -1] == 0):
            data[i, -1] = -1
    return data[:, :2], data[:, -1]


X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
clf = SVC(kernel='linear')
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))

data = pd.DataFrame([[1, 2], [2, 3], [3, 3], [2, 1], [3, 2]])
label = pd.DataFrame([1, 1, 1, -1, -1])
plt.scatter(data[:3][0], data[:3][1], c='r', marker='o', label='+')
plt.scatter(data[3:][0], data[3:][1], c='g', marker='x', label='-')

X = data
y = label
clf.fit(X, y)

xi = np.linspace(-1, 4, 20)
yi = (clf.coef_[0][0] * xi + clf.intercept_) / (-clf.coef_[0][1])
plt.plot(xi, yi, 'b', label='分离超平面')
plt.legend()
plt.title("练习7.2")
plt.rcParams['font.sans-serif'] = 'SimHei'  # 消除中文乱码
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号
plt.show()
print(clf.support_vectors_)
print(clf.coef_)
print(clf.intercept_)
print(clf.support_)
print(clf.n_support_)

[[2. 1.]	# 支持向量
 [3. 2.]	# 支持向量
 [1. 2.]	# 支持向量
 [3. 3.]]	# 支持向量
[[-0.6664  1.3328]]	# w
[-0.99946667]	# b
[3 4 0 2]
[2 2]

在这里插入图片描述

Michael阿明

发布了743 篇原创文章 · 获赞 917 · 访问量 26万+

他的留言板关注