支持向量机Support Vector Machine

在样本空间中，划分超平面的方程描述如下：

$$w^Tx + b = 0$$ 其中 w为法向量，决定了超平面的方向，b为位移项，决定了超平面与原点的距离。

样本空间的点x到这个划分超平面距离为(x’为x在超平面上的投影) :

$$d = \frac{w}{||w||}(x-x') = \frac{w^Tx-w^Tx'}{||w||} = \frac{|w^Tx +b|}{||w||}$$

很明显，不同的超平面方向和位移项对分类鲁棒性不同，一般而言其间距(margin)越宽泛化能力也更好。

对于正确分类的样本，总有：

$$\left\{\begin{matrix} w^Tx_i + b>0, & y_i=+1; & \\ w^Tx_i + b<0, & y_i=-1 & \end{matrix}\right.$$

且存在缩放系数 $w = \zeta w$使下式成立:

$$\left\{\begin{matrix} w^Tx_i + b>0, & y_i=+1; & \qquad(1) \\ w^Tx_i + b<0, & y_i=-1 & \end{matrix}\right.$$
如图一中正好处于边界上使得等号成立的样本点被称为 支持向量(SV: Support Vecto)。

易得灰色间隔的宽度为 $2 \cdot \frac{1}{||w||}$， 优化的问题是改变w,b的值使得正确分类的同时间距最大：

$$\max\limits_{w,b} 2 \cdot \frac{1}{||w||} \\ s.t. \quad y_i(w^Tx_i + b)>=1 \quad即(1)式表示正确分类$$
上式等价于 : $$\min\limits_{w,b} \frac{1}{2} \cdot ||w|| \qquad(2) \\ s.t. \quad y_i(w^Tx_i + b)>=1$$
虽然这是一个凸优化（二次导数>=0）问题，但是涉及多个变量求解较慢，引入拉格朗日乘子：
$$L(w,b,a) = \frac{1}{2} \cdot ||w|| + \sum_i^m a_i(1-y_i(w^Tx_i+b))$$
注意到上式中 $1-y_i(w^Tx_i+b) <=0$ ，若添加约束条件 $a_i >=0$则后半部分始终<=0，即： $$\max\limits_{a} L(w,b,a) <= \frac{1}{2} \cdot ||w|| \\ s.t. \quad a_i>=0$$
可以看到拉格朗日乘子法就是: $g(x) = 原函数 f(x) + \sum a_i(a_i>=0) * 约束 h_i(x)$

也就是说求$\min\limits_{w,b} \frac{1}{2} \cdot ||w||$ 相当于求 $\min\limits_{w,b} (\max\limits_{a} L(w,b,a) )$

利用对偶问题，易证明下面的(3)式始终成立，那么即时(3)式的右边取最大值，不等式也依然成立即(4)式成立。

对偶问题呢？因为在约束面上当连续可导时，当取等最大或最小值时导数一定为0。而且利用偏导都为0得到的式子带入乘子式可以消去一部分变量，使得计算简单化。

例如令L(w,b,a)求偏导得到：

$$\frac{\partial L}{\partial w} = \sum a_iy_ix_i \\ 0 = \sum a_iy_i$$
带入可得 $\min\limits_{w,b} L(w,b, a) = \sum a_i - 1/2\sum |a_iy_ix_i|^2$。发现只有一个变量a。也就是说 如果利用 $\min\limits_{w,b} L(w,b, a)$ 求偏导为0可能消掉2个变量，而利用 $\max\limits_{a} L(w,b, a)$ 只能消掉一个变量

只剩下一个变量a那么求下式也就比较简单了：

$$\max\limits_{a} (\min\limits_{w,b} L(w,b, a)) = \max\limits_{a} \sum a_i - \frac{1}{2} \sum_i^m\sum_j^m a_i a_j y_i y_j x_i^T x_j$$ 另外需要满足的条件(KKT)是：
$$\left\{\begin{matrix} y_i(wx_i+b)>=0; & \qquad 正确分类约束 \\ ai>=0; & \qquad 拉格朗日乘子系数约束 \\ a_i[y_i(wx_i+b)-1] = 0; & \end{matrix}\right.$$ 不等式是若对偶关系，当等号成立时是强对偶关系，而且等号应该是在间距的边界上成立。因此最后一个是 最值在边界上的约束，如样本点不在边界上a_i=0忽略其影响，否则若在边界上必有y_i(wx_i+b)-1=0，其影响因子a_i可不为0。

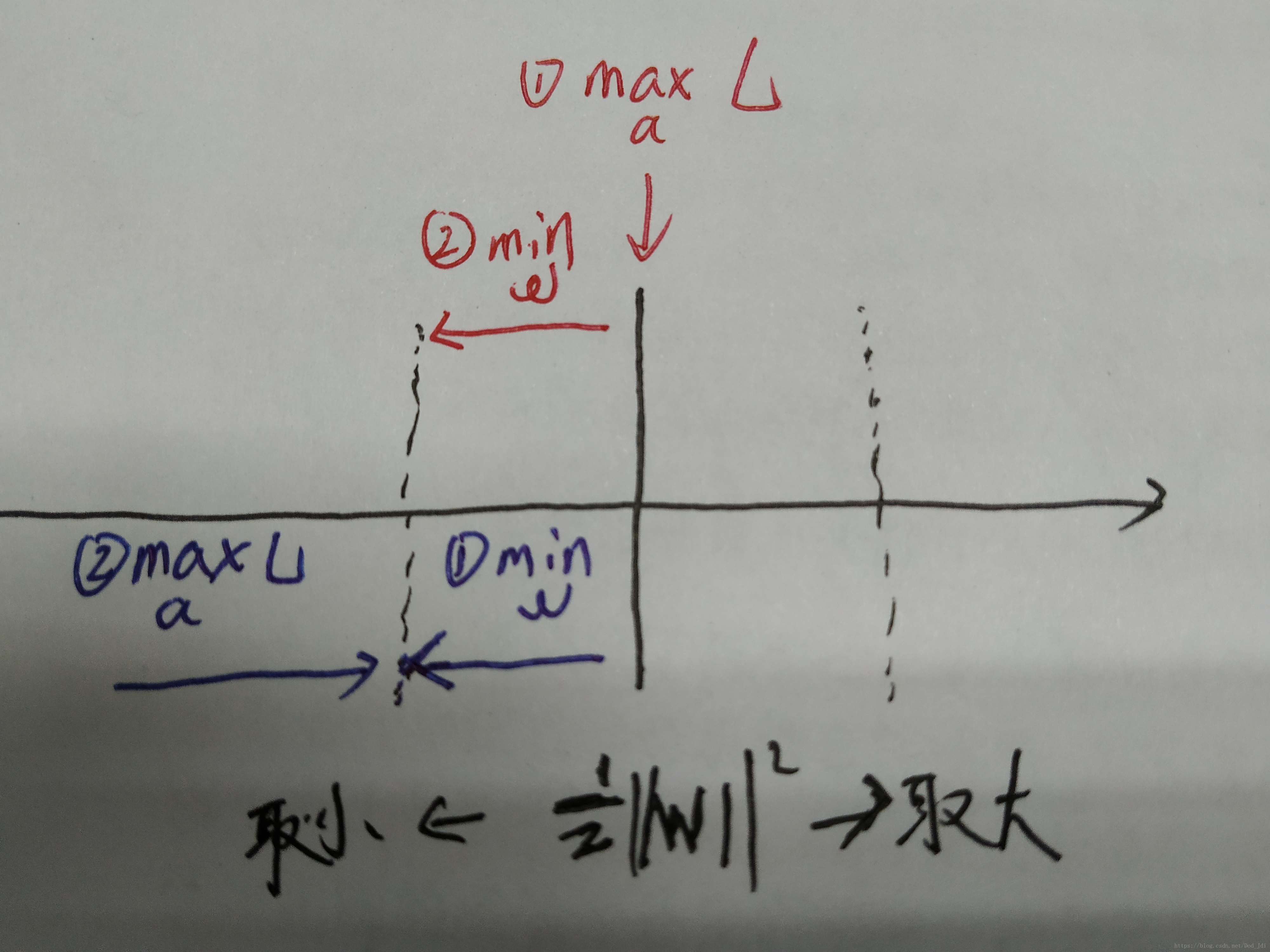
对偶的理解： 几何含义如下，先$max L$ 就是把其和w绑在一块（等于情况）再把w往左移（min），而max(min)则是先左移了w再把L从左往w靠。计算的角度来说则是偏导为0带入消元法。