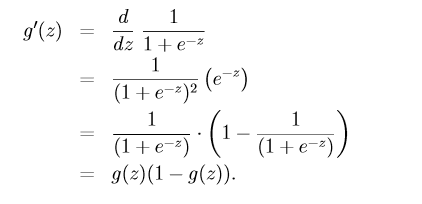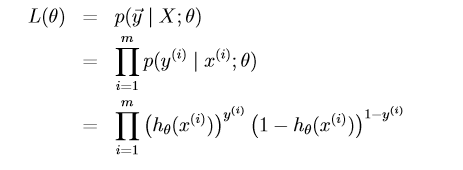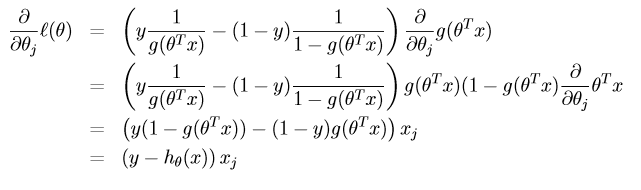Logistic Regression（逻辑回归）

介绍

逻辑回归虽然称为回归，但它却是一个分类算法，一个用来解决二分类问题的算法，它通过将线性回归预测出的值映射到 {0,1} 上来实现分类的（0叫做负类，1叫做正类）。这是一个很简单的二分类算法，它的思想也很容易理解。

逻辑回归与线性回归的流程很相似：

1. 构造预测函数。根据训练的样本数据，构造模型来预测输入变量 x 的输出值（或类别）。
2. 构造损失函数或似然函数。要使模型的参数最大程度符合实际模型，就要使损失函数值最小
3. 求损失函数的最小值或似然函数的最大值。损失函数的最小值（或似然函数的最大值）所对应的参数即为模型的最优参数。根据所求参数值，即可对输入变量 x 进行预测。

Sigmoid函数

通常，我们在预测值的时候，线性回归是最常用的方法。但由于线性回归输出的值是连续的，因此并不适合解决分类问题。然而，我们可以通过将连续值映射到离散值，来使得我们可以利用线性回归的方法来解决分类问题。这时我们就需要一个映射函数，最常使用的就是 Sigmoid 函数（也可以称为 Logistic 函数）：

$g(z) = \frac1{1 + e^{-z}}$

该函数就可以实现将连续值映射到 （-1,1） 区间，下图是它的图像：

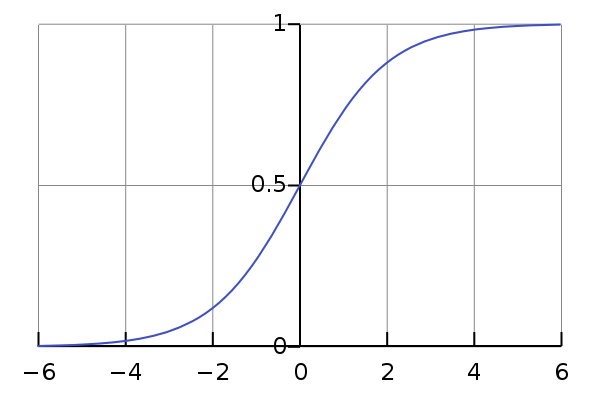
之所以使用该函数，是因为它具有其他很好的性质，这里只利用它的映射性质就足够了。

它的导数形式为：

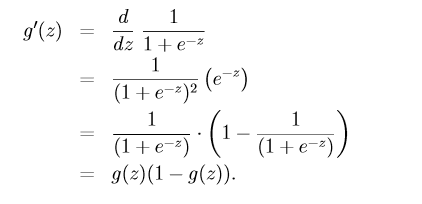
似然函数

逻辑回归的预测函数为：

$h_\theta(x) = g(\theta^Tx) = \frac1{1 + e^{-\theta^Tx}}$

这个预测值，也可以理解为变量 x 属于哪一个分类的概率值，即：

$P(y = 1| x;\theta) = h_\theta(x)\\ \ \ \ \ \ \ \ P(y = 0| x;\theta) = 1 - h_\theta(x)$

根据伯努利公式，可以将这两个写成一个式子：

$P(y | x;\theta) = {(h_\theta(x))}^y{(1 - h_\theta(x))}^{1 - y}$

假设有 m 个训练样本，则似然函数可以写为：

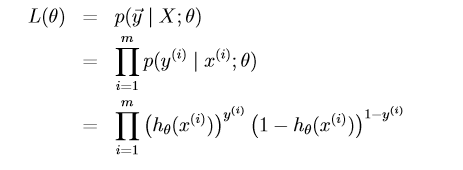
梯度下降法求解

准确地说，求解似然函数最大值的方法是利用 “梯度上升” 的方法，与梯度下降法相似，梯度上升法也是不断地找到该位置的最优方向前进，只不过梯度上升是每次找到该位置可以到达最高的方向。

由于需要求偏导，为了使求导简单，这里取似然函数的对数形式：

$l(\theta) = logL(\theta) =\sum_{i = 1}^m (y^{(i)}logh(x^{(i)}) + (1 - y^{i})log(1 - h(x^{(i)})))$

对 $l(\theta)$ 进行求导：

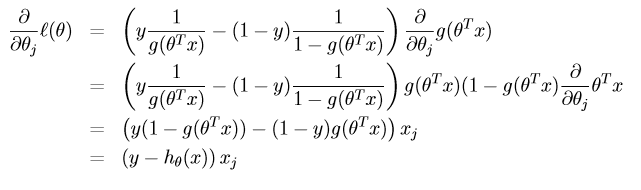
根据梯度上升法： $\theta = \theta + \alpha\nabla l(\theta)$ 有：

$\theta_j = \theta_j + \alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)}$

总结

Logistic回归最大的优点就是实现简单，计算量小；但也有一个最大的缺陷，就是只能解决二分类问题，若要解决多分类问题，可以进行扩展，典型的算法就是 softmax 方法，这里就不详细介绍了，以后再写。

最近刚开始学习机器学习，想通过博客的方式写一些自己的理解，如果有错误的地方，希望大家给予纠正，谢谢。

参考文献

1. 机器学习–Logistic回归计算过程的推导
2. 机器学习&数据挖掘笔记_16（常见面试之机器学习算法思想简单梳理）
3. 机器学习算法–逻辑回归原理介绍