强化学习笔记（2）—— 马尔科夫决策过程 MDP

• 参考：周博磊老师的教程

---

1. 马尔可夫链

1.1 马尔可夫性质/无后效性（Markov Property）

• 定义：过程或系统在时刻 $t_0$ 所处的状态为已知的情况下，在时刻 $t>t_0$ 所处状态的条件分布与过程在时刻 $t_0$ 之前所处的状态无关。通俗的说，就是系统下一步状态仅取决于当前状态，而与历史状态无关

• 形式化定义：

  1. 定义状态历史： h t = { s 1 , s 2 , s 3 , . . . , s t } h_t = \{s_1,s_2,s_3, ...,s_t\} ht​={ s1​,s2​,s3​,...,st​}
  2. 定义马尔科夫性：如果系统满足以下性质，我们称这个系统具有马尔科夫性
     $$\begin{gathered} P(s_{t+1}|s_t)=P(s_{t+1}|h_t) \\ P(s_{t+1}|s_t,a_t)=P(s_{t+1}|h_t,a_t) \end{gathered}$$

• 需要说明的是，这种性质不是为了简化而简化，而是有一定依据的。比如我们都知道的一个走迷宫技巧：在每个岔路总是选择拐弯（这会执行一个深度优先搜索），把我们所在的不同位置看作不同状态，则每个新状态只与当前状态有关

1.2 马尔可夫过程（Markov Process / MP）

• 定义：具有马尔科夫性的随机过程称为马尔科夫过程
• 马尔科夫过程描述的是系统从一个状态到另一个状态转换的随机过程。该过程要求具备马尔可夫性，也就是下一状态的概率分布只与当前的状态有关，而与时间序列中其他前面的事件无关。

1.3 马尔可夫链（Markov Chain）

• 马尔可夫链描述了一个具有马尔可夫性质的系统的状态转移情况

• 把系统的所有状态画成若干个点，然后用箭头和转移概率把它们连接起来，就得到了这个系统的马尔可夫链

• 示例：下图是一个具有4个状态的系统，状态间以一定的概率转移，且这个概率仅取决于当前状态

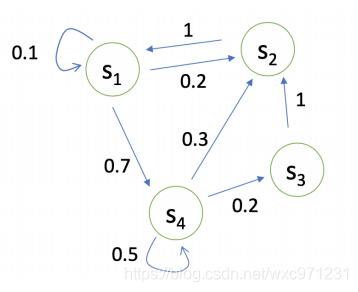
• 形式化描述

  1. 状态向量： X n = { x 1 n , x 2 n , . . . , x k n } X^n = \{x_1^n,x_2^n,...,x_k^n\} Xn={ x1n​,x2n​,...,xkn​}

     • 状态向量描述了第n次观测时，系统可能处于各个状态的概率
     • 系统的可能状态数有k个，$x_1^n,x_2^n,...,x_k^n$都是概率，它们的和为1
     • $X^0$ 被称为初始状态

  2. 状态转移矩阵

     1. 我们用$P_{s{s}^{\prime }}$表示从状态s转移到状态s’的概率，即$P_{s{s}^{\prime }}=P(S_{t+1}=s^{\prime }|S_t=s)$

     2. 这样就可以用矩阵的形式表示所有状态的转移概率
        
        称这个矩阵为 “状态转移矩阵”

     3. 注意这个矩阵的行和/列和都是1

  3. 根据无后效性，我们可以得出
     $$X^n=X^{n-1}P$$
     于是有
     $$X^n=X^0{P}^n$$
     所以只要求出状态转移矩阵P，这个系统（马尔可夫模型）就确定了

• 利用马尔可夫链（准确说是利用状态转移矩阵），我们就可以从初始状态预测系统未来任意时刻可能处于的状态概率分布。这个预测本质就是状态转移矩阵的连乘，因此这还涉及一个收敛性的问题，这里不展开讨论，可以参考：数学模型——初步理解马尔可夫链（Markov chain）

2. 马尔可夫奖励过程（MRP）

• 简单看，MRP = Markov chain + reward function

2.1 基础概念

1. episode（轨迹）：对马尔可夫链采样得到一个状态序列，称为一个轨迹
2. Horizon：一个轨迹的最大长度（number of maximum time step），可以是$\infty$，否则称为有限马尔可夫奖励过程
3. Return（$G_t$）：Horizon中从第 t 步到最后的奖励加权和
   $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T$$
   这里的 $\gamma \in [0,1]$ 就是下面MRP定义中的折扣系数。这个return $G_t$ 代表着未来可能获取奖励的加权和
4. 状态价值函数V(s)：$V(S_t)$ 代表第 t 步处于状态 s 时的return的期望，即 “未来可能获取奖励的加权和” 的当前期望值
   $$V(S_t)=V(s)=\mathbb{E}[G_t|S_t=s]=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...++{\gamma }^{T-t-1}{R}_T|S_t=s]$$
   $V(s)$也常记为$V(S_t)$ 或 $V_S$ ，这是对MRP中状态的一个评鉴指标。它描述了进入状态s可以获取的 “长期价值” （long-term value），这真正表示了进入状态s有多好

2.2 定义

• 马尔可夫奖励过程MRP是一个四元组 $<S,P,R,\gamma >$

  1. S：有限状态集
  2. P：状态转移矩阵，定义了 $P_{s{s}^{\prime }}=P(S_{t+1}=s^{\prime }|S_t=s)$
  3. R：奖励函数 $R(S_t=s)=\mathbb{E}[R_{t+1}|S_t=s]$
  4. $\gamma$：折扣系数，$\gamma \in [0,1]$

• 说明

  1. 奖励函数$R(S_t=s)$定义某时刻t处于状态s下的奖励为：离开t时刻时能获得的奖励的期望。式子里写$R_{t+1}$而不是$R_t$ 可能会引起困惑，其实这只是一个约定。我们一般倾向于任务离开而非进入 $S_t$ 这个状态时才能获取奖励。可以把$R_{t+1}$ 理解为离开 $t$ 时刻时获得的奖励，也可以简单地把$R(s)$理解为进入状态s可以获得的奖励。通常会人为地给$R(s)$设定一个值，所以这个期望一般不用算
  2. 为什么有折扣系数 $\gamma$：
     1. 避免带环的Markov chain中出现无穷的奖励
     2. 看上面V(s)的公式，越未来的状态乘上的折扣系数越多，这是对于未来奖励不确定性的体现
     3. 人和动物的行为中都表现出对即刻奖励的追求，$\gamma$ 可以模拟这一点，它使模型更看重短期奖励（权重更高）
     4. 某些情况下也会使用不折价的MRP， $\gamma =1$ 时意味着任意时刻的奖励都同样重要；$\gamma =0$ 时意味只考虑当前奖励
  3. 折扣系数 $\gamma$ 一般用作超参数，可以通过调整它获取不同行为的agent

2.3 MRP的示例

2.4 状态价值函数 V 如何计算

2.4.1 蒙特卡洛方法

• 价值函数$V(s)=\mathbb{E}[G_t|S_t=s]$ 就是求$G_t$ 的期望，可以从状态s开始采样多个轨迹，分别计算 $G_t$ 然后取均值
• 伪代码如下
  

2.4.2 利用Bellman等式

• 注意：以下用 $S_t$ 或 s 代表当前时刻 t 的状态，$S_{t+1}$ 或 s’ 代表下一时刻的状态

2.4.2.1 Bellman等式

$$V(S_t)=R(S_t)+\gamma \sum _{S_{t+1}\in S}P(S_{t+1}|S_t)V(S_{t+1})$$

• 这个式子可以分成两部分，$R(S_t)$代表当前状态的立即奖励，后半边可以看做未来奖励的加权和

• 这个式子满足递归特性，即 “这一步的未来奖励期望 = 这一步奖励 + 下一步的未来奖励期望”，可以写成递归矩阵形式
  $$V=R+\gamma PV$$
  

• Bellman等式描述了状态之间的迭代关系，知道了下一步所有可能状态的 V(s’)，即可解出当前状态的 V(s)

2.4.2.2 推导

$$\begin{array}{rl}V(S_t)& =\mathbb{E}[G_t|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & =\mathbb{E}[R_{t+1}+\gamma V(S_{t+1})|S_t=s]\\ & =R(S_t)+\gamma \sum _{S_{t+1}\in S}P(S_{t+1}|S_t)V(S_{t+1})\end{array}$$

• 注意$R_{t+1}$代表 t 时刻最后离开状态$S_t$时获得的奖励，就是状态$S_t$的奖励$R(S_t)$

2.4.2.3 用Bellman等式解价值函数

1. 直接解：$V=R+\gamma PV$是一个线性方程，可以通过矩阵求逆直接解，即
   $$V=(1-\gamma P){)}^{-1}R$$
   但是矩阵求逆的复杂度为$o(N^3)$，所以直接求解的方式仅适用于小规模MRP问题

2. 递推方式求解：适用于状态多的MRP问题，常用的方法有3个

   1. 动态规划（Dynamic Programming）
      
      这个就是不断用Bellman公式进行迭代计算，直到V收敛为止

   2. 蒙特卡洛（Monte-Carlo evaluation），详见上文

   3. TD学习 （Temporal-Difference learning），这可以看作以上两个的结合

3. 马尔可夫决策过程（MDP）

• 简单看，MDP = MRP + Policy，MDP是有决策的MRP

3.1 定义

• 马尔可夫决策过程MDP是一个五元组 $<S,A,P^a,R,\gamma >$
  1. S：有限状态集
  2. A：有限动作集
  3. $P^a$：状态转移矩阵，定义了 $P_{s{s}^{\prime }}=P(S_{t+1}=s^{\prime }|S_t=s,A_t=a)$
  4. R：奖励函数 $R(S_t=s,A_t=a)=\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$
  5. $\gamma$：折扣系数，$\gamma \in [0,1]$
• MDP中的Policy（$\pi$）
  1. policy指定了某个状态s下该采取的动作a
  2. 给定一个状态s，Policy给出一个动作的概率分布（ distribution over actions）
     $$\pi (a|s)=P(A_t=a|S_t=s)$$
  3. Policy最终给出的是从状态s的动作分布$\pi (a|s)$ 上采样的一个action
  4. Policy是静态的（时间独立），每个时刻的动作$A_t$ 都是$\pi (a|s)$上的一个采样

3.2 MDP和MRP

3.2.1 从MDP转换到MRP

1. 给出MDP $<S,A,P,R,\gamma >$ 以及 Policy $\pi$

2. 使用S、P 和 $\pi$ 可以构造 马尔可夫过程MP：$<S,P^{\pi }>$，这对应一个 “状态序列” $S_1,S_2,...$

3. 使用S,P,R,$\gamma$ 和 $\pi$ 可以构造 马尔可夫奖励过程MRP：$<S,P^{\pi },R^{\pi },\gamma >$，这里$P^{\pi },R^{\pi }$都是把某个状态下所有动作做加权和（求期望），从而消除了动作A：
   $$\begin{gathered} P^{\pi }(s^{\prime }|s)=\sum _{a\in A}\pi (a|s)P(s^{\prime }|s,a) \\ {R}^{\pi }(s)=\sum _{a\in A}\pi (a|s)R(s,a) \end{gathered}$$

   这对应一个 “状态奖励序列” $S_0,R_1,S_1,R_2,...$

4. MDP本身对应一个 “状态动作奖励序列”：$S_0,A_0,R_1,S_1,A_1,R_2,...$

3.2.2 对比MDP和MRP

• 相比MRP，MDP从状态s出发后首先要在动作分布中选一个action a，然后才能得到转移概率P，进而转移到新状态s’。“选action” 这一环就是 “决策”
  
• 有一个很经典的比喻
  • MRP好像一个纸船，在马尔可夫链上的各个状态之间按概率转移矩阵随波逐流
  • MDP好像有人在架船，它有Policy，会根据当前的状态采取不同的action，进而影响下一个进入的状态

3.3 MDP的 价值函数 & 动作价值函数

1. 价值函数$V^{\pi }(s)$：从状态s开始，以Policy $\pi$ 运行的return $G_t$ 的期望
   $$V^{\pi }(s)={\mathbb{E}}_{\pi }(G_t|S_t=s)$$

2. 动作价值函数 $q^{\pi }(s,a)$：从状态s，采取动作a开始，以Policy $\pi$ 运行的return $G_t$ 的期望
   $$q^{\pi }(s,a)={\mathbb{E}}_{\pi }(G_t|S_t=s,A_t=a)$$

3. 二者关系：把每个状态s下所有可能采取a的价值 $q^{\pi }(s,a)$ 求和（就是求期望），即得s的价值$V^{\pi }(s)$
   $$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)q^{\pi }(s,a)$$

3.4 Bellman等式

• 类似MRP中的Bellman等式，先把return $G_t$和$q$ 分解成立即奖励和未来奖励两部分
  $$\begin{array}{rl}{G}_t& =R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ & =R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)\\ & =R_{t+1}+\gamma G_{t+1}\end{array}$$

• 所以有
  $$\begin{array}{rl}{V}^{\pi }(S_t)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma V^{\pi }(S_{t+1})|s]\end{array}$$

  $$\begin{array}{rl}{q}^{\pi }(S_t,A_t)& ={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|s,a]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma q^{\pi }(S_{t+1},A_{t+1})|s,a]\end{array}$$

• 对于$q^{\pi }$固定a加和s，对于$V^{\pi }$固定s加和a，去掉期望符号后得到二者关系

  1. 关系式
     $$q^{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })$$

     $$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)q^{\pi }(s,a)$$

  2. 看图理解一下$q^{\pi }$和$V^{\pi }$的关系
     
     

• 再上面二式互相带入，即得相邻时刻 $q^{\pi }$ 和相邻时刻 $V^{\pi }$ 的关系

  1. 关系式
     $$q^{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)\sum _{a\in A}\pi (a^{\prime }|s^{\prime })q^{\pi }(s^{\prime },a^{\prime })$$

     $$V^{\pi }(s)=\sum _{a\in A}\pi (a|s)[R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })]$$

  2. 看图理解一下