在强化学习(一)模型基础中,我们讲到了强化学习模型的8个基本要素。但是仅凭这些要素还是无法使用强化学习来帮助我们解决问题的, 在讲到模型训练前,模型的简化也很重要,这一篇主要就是讲如何利用马尔科夫决策过程(Markov Decision Process,以下简称MDP)来简化强化学习的建模。
MDP这一篇对应Sutton书的第三章和UCL强化学习课程的第二讲。
1. 强化学习引入MDP的原因
强化学习的8个要素我们在第一节已经讲了。其中的第七个是环境的状态转化模型,它可以表示为一个概率模型,即在状态$s$下采取动作$a$,转到下一个状态$s'$的概率,表示为$P_{ss'}^a$。
如果按照真实的环境转化过程看,转化到下一个状态$s'$的概率既与上一个状态$s$有关,还与上上个状态,以及上上上个状态有关。这一会导致我们的环境转化模型非常复杂,复杂到难以建模。因此我们需要对强化学习的环境转化模型进行简化。简化的方法就是假设状态转化的马尔科夫性,也就是假设转化到下一个状态$s'$的概率仅与上一个状态$s$有关,与之前的状态无关。用公式表示就是:$$P_{ss'}^a = \mathbb{E}(S_{t+1}=s'|S_t=s, A_t=a)$$
对于马尔科夫性本身,我之前讲过的隐马尔科夫模型HMM(一)HMM模型,条件随机场CRF(一)从随机场到线性链条件随机场以及MCMC(二)马尔科夫链都有讲到。它本身是一个比较简单的假设,因此这里就不专门对“马尔可夫性”做专门的讲述了。
除了对于环境的状态转化模型这个因素做马尔科夫假设外,我们还对强化学习第四个要素个体的策略(policy)$\pi$也做了马尔科夫假设。即在状态$s$时采取动作$a$的概率仅与当前状态$s$有关,与其他的要素无关。用公式表示就是$$\pi(a|s) = P(A_t=a | S_t=s)$$
对于第五个要素,价值函数$v_{\pi}(s)$也是一样, $v_{\pi}(s)$现在仅仅依赖于当前状态了,那么现在价值函数$v_{\pi}(s)$表示为:$$v_{\pi}(s) = \mathbb{E}_{\pi}(G_t|S_t=s ) = \mathbb{E}_{\pi}(R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3}+...|S_t=s)$$
其中,$G_t$代表收获(return), 是一个MDP中从某一个状态$S_t$开始采样直到终止状态时所有奖励的有衰减的之和。
2. MDP的价值函数与贝尔曼方程
对于MDP,我们在第一节里已经讲到了它的价值函数$v_{\pi}(s)$的表达式。但是这个表达式没有考虑到所采用的动作$a$带来的价值影响,因此我们除了$v_{\pi}(s)$这个状态价值函数外,还有一个动作价值函数$q_{\pi}(s,a)$,即:$$q_{\pi}(s,a) = \mathbb{E}_{\pi}(G_t|S_t=s, A_t=a) = \mathbb{E}_{\pi}(R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3}+...|S_t=s,A_t=a)$$
根据价值函数的表达式,我们可以推导出价值函数基于状态的递推关系,比如对于状态价值函数$v_{\pi}(s)$,可以发现:$$\begin{align} v_{\pi}(s) &= \mathbb{E}_{\pi}(R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3}+...|S_t=s) \\ &= \mathbb{E}_{\pi}(R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3}+...)|S_t=s) \\ &= \mathbb{E}_{\pi}(R_{t+1} + \gamma G_{t+1} | S_t=s) \\ &= \mathbb{E}_{\pi}(R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t=s) \end{align}$$
也就是说,在$t$时刻的状态$S_t$和$t+1$时刻的状态$S_{t+1}$是满足递推关系的,即:$$v_{\pi}(s) = \mathbb{E}_{\pi}(R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t=s) $$
这个递推式子我们一般将它叫做贝尔曼方程。这个式子告诉我们,一个状态的价值由该状态的奖励以及后续状态价值按一定的衰减比例联合组成。
同样的方法,我们可以得到动作价值函数$q_{\pi}(s,a)$的贝尔曼方程:$$q_{\pi}(s,a) = \mathbb{E}_{\pi}(R_{t+1} + \gamma q_{\pi}(S_{t+1},A_{t+1}) | S_t=s, A_t=a) $$
3. 状态价值函数与动作价值函数的递推关系
根据动作价值函数$q_{\pi}(s,a)$和状态价值函数$v_{\pi}(s)$的定义,我们很容易得到他们之间的转化关系公式:$$v_{\pi}(s) = \sum\limits_{a \in A} \pi(a|s)q_{\pi}(s,a)$$
也就是说,状态价值函数是所有动作价值函数基于策略$\pi$的期望。通俗说就是某状态下所有状态动作价值乘以该动作出现的概率,最后求和,就得到了对应的状态价值。
反过来,利用上贝尔曼方程,我们也很容易从状态价值函数$v_{\pi}(s)$表示动作价值函数$q_{\pi}(s,a)$,即:$$q_{\pi}(s,a) = R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{\pi}(s')$$
通俗说就是状态动作价值有两部分相加组成,第一部分是即时奖励,第二部分是环境所有可能出现的下一个状态的概率乘以该下一状态的状态价值,最后求和,并加上衰减。
这两个转化过程也可以从下图中直观的看出:
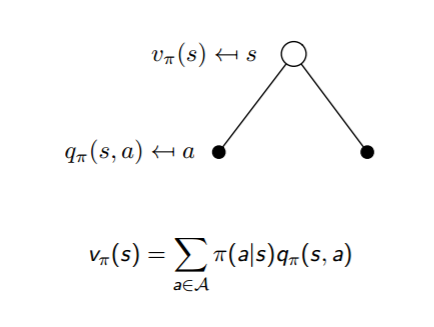
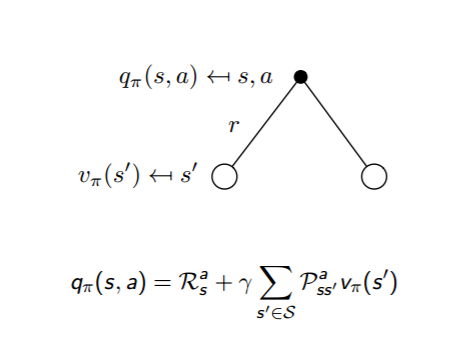
4. 最优价值函数
解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其它策略都要多的收获,这个最优策略我们可以用 $\pi^{*}$表示。一旦找到这个最优策略$\pi^{*}$,那么我们就解决了这个强化学习问题。一般来说,比较难去找到一个最优策略,但是可以通过比较若干不同策略的优劣来确定一个较好的策略,也就是局部最优解。
如何比较策略的优劣呢?一般是通过对应的价值函数来比较的,也就是说,寻找较优策略可以通过寻找较优的价值函数来完成。可以定义最优状态价值函数是所有策略下产生的众多状态价值函数中的最大者,即:$$v_{*}(s) = \max_{\pi}v_{\pi}(s)$$
同理也可以定义最优动作价值函数是所有策略下产生的众多动作状态价值函数中的最大者,即:$$q_{*}(s,a) = \max_{\pi}q_{\pi}(s,a)$$
只要我们找到了最大的状态价值函数或者动作价值函数,那么对应的策略$\pi^{*}$就是我们强化学习问题的解。同时,利用状态价值函数和动作价值函数之间的关系,我们也可以得到:$$v_{*}(s) = \max_{a}q_{*}(s,a) $$
反过来的最优价值函数关系也很容易得到:$$q_{*}(s,a) = R_s^a + \gamma \sum\limits_{s' \in S}P_{ss'}^av_{*}(s')$$
5. MDP实例
上面的公式有点多,需要一些时间慢慢消化,这里给出一个UCL讲义上实际的例子,看看具体我们如何利用MDP来求解最优的价值函数。
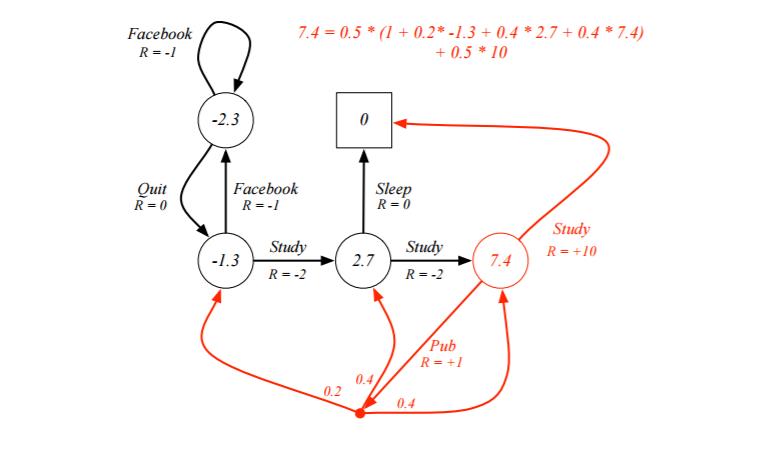
例子是一个学生学习考试的MDP。里面-1.3那个位置是起点,0那个位置是终点。上面的动作有study, pub, facebook, quit, sleep,每个状态动作对应的即时奖励R已经标出来了。我们的目标是找到最优的价值函数,顺便找出最优的策略。