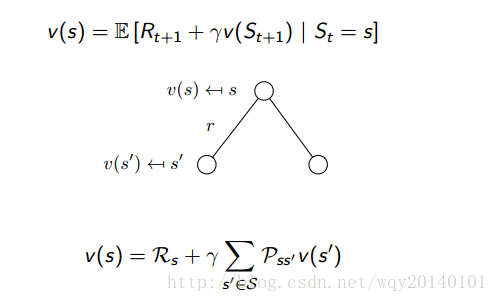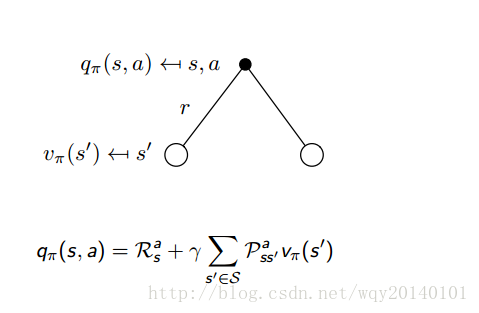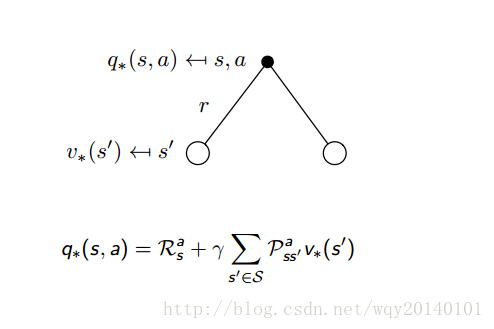强化学习（二）——MDP：马尔科夫决策过程

前言

本文主要采用了David Silver的RL授课ppt（个人认为英文的ppt比中文更加生动准确），与个人听课理解总结。本文详细地介绍了马尔科夫决策相关理论和目标。读懂本文的前提是已经掌握理解了上一节：http://blog.csdn.net/wqy20140101/article/details/78562890 ok，我们开始吧！

马尔科夫状态

在我们所处的环境中，接下来会发生什么事情，只取决于上一时刻的状态，而不是取决于之前所有的状态。未来只有当前状态决定（为什么，请参看上一篇简介博客：http://blog.csdn.net/wqy20140101/article/details/78562890）

状态转移概率

从当前状态转移到下一个状态的概率。

马尔科夫过程##

马尔科夫过程是一个随机的过程，由一系列的具有马尔科夫状态的随机状态组成。其中，状态和概率分布完整地定义了整个系统动态变化的过程。

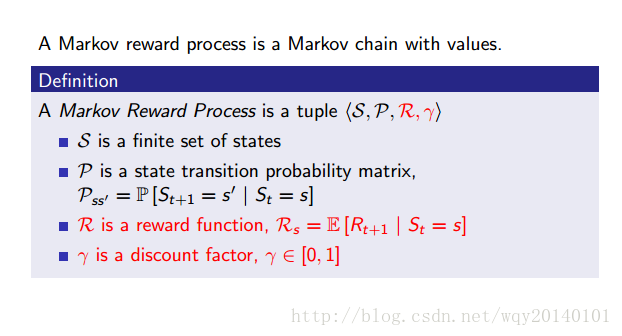
马尔科夫奖励过程

什么是马尔科夫奖励过程

带有value判断的马尔科夫链就是马尔科夫奖励过程。

目标函数$G_t$

我们关心的是 $reward$在整个过程中的总和，我们的目标就是最大化 $return$的总额。为了长期表现良好，我们不仅需要考虑即时奖励，还有我们将得到的未来奖励。 $G_t$表示的是在某个确定的随机序列样本中，所有的时间步的 $return$ 之和：

$G_t=\sum_{k=0}^\infty\gamma^kR_{t+k+1}$为什么引入折扣因子 $\gamma$?但是由于我们的环境是随机的，我们永远无法确定如果我们在下一个相同的动作之后能否得到一样的奖励。时间愈往前，分歧也愈多。因此，这时候就要利用折扣未来奖励来代替。

$\gamma$范围是[0,1]，代表未来某一步的奖励在现在看来，贡献比例是多少，度量我们有多倾向于更接近当前时间的 $reward$。如果我们将贴现因子定义为 $\gamma$=0，那么我们的策略将会过于短浅，即完全基于即时奖励。如果我们希望平衡即时与未来奖励，那么贴现因子应该近似于 $\gamma$=0.9。如果我们的环境是确定的，相同的动作总是导致相同的奖励，那么我们可以将贴现因子定义为 γ=1。同时， $\gamma$的引入也是控制求和项有限的方式。

Value Function

它表明目前所在的 $state$有多好。它是所有随机序列在当前 $state$下，能获得 $reward$之和的期望：
$v(s)=E[G_t|S_t=s]$
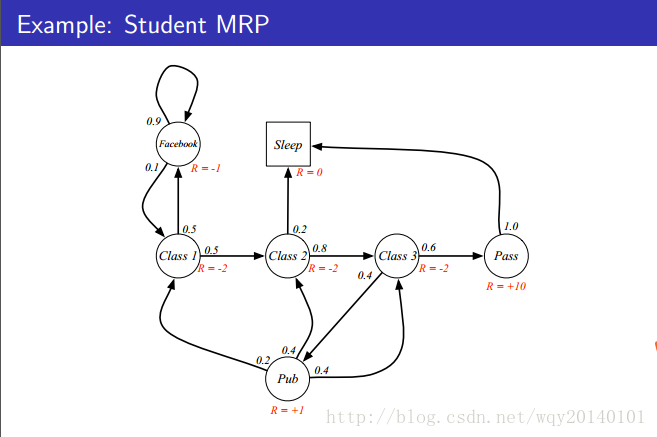
举例并通过计算来再次说明 $G_t$和 $v$的关系：

注：带箭头线上面的小数是我们做某件事的概率，其中，sleep表示的是马尔科夫过程的最终状态，你不用把它看为特殊的机制，只需要看成一个自环，是一种一直在吸收的状态。

纠正：这里的v1改为g1
解释：每一个simple可以看做一个随机序列，该序列以一定的概率分布在序列上进行状态转移。上面的图片展示了，对于不同的随机序列，g的计算过程，对应的v1就是取这些g1的期望。g是随机的，但value function不是随机的。现在你知道为什么前面说的v是用来表示目前的状态有多好了吧(#^.#)

Bellman Equation（贝尔曼方程）

从上图的推导我们可以看出，该状态s下的value function，等于预计的立即回报，加上下一个state的value function的返回值。同时，我们用一种Backup Diagram，又称为前向搜索图，来形象化地理解贝尔曼方程。首先是值函数的贝尔曼方程：

解释：在当前状态是s，值函数为v，v就等于立即奖励加上下一个状态折扣后的值函数。其中， $R_s$为即时奖励，也就是离开状态s时我们立刻能够获得的奖励。由于状态转移存在一定的概率分布，所以下一个状态折扣后的期望就等于转移概率乘以转移状态的值函数。

马尔科夫决策过程

什么是马尔科夫决策过程

马尔科夫决策过程是**包含决策**的马尔科夫奖励过程。

状态值函数告诉我们达到某一个 $state$对实现目标有多好，行为值函数告诉我们，在某一个 $state$采取某个 $action$ 对实现目标有多好。

Value Function(值函数)

MDP有两种值函数，一种是状态值函数，一种是动作值函数，均是在策略 $\pi$ 下讨论的。动作值函数只是在状态值函数表达里面加入了动作。明显地，动作值函数才是我们关心的变量。如果我们找到了动作值函数，进一步找到最优的，从而制定出我们的行动策略。

状态值函数： $v_\pi(s)=E[G_t|S_t=s]$ 动作值函数： $q_\pi(s)=E[G_t|S_t=s,A_t=a]$ 动作值函数代表，在该状态下，采取action有多好。有些地方把动作值函数记为大写的Q，没关系，意思都是一样的。

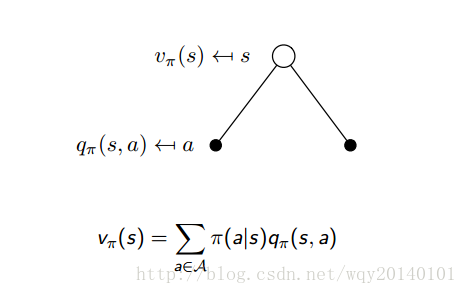
Bellman Expectation Equation(贝尔曼期望方程)

从上面的策略$\pi$下的值函数，可以得到对应的贝尔曼方程。状态值函数d的贝尔曼方程：$$v_\pi(s)=E[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s]$$动作值函数的贝尔曼方程$$q_\pi(s)=E[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s,A_t=a]$$我们再看看状态值函数和动作值函数在策略下的backup diagram。它能帮助我们理解v和q是如何关联的。其中空心圆代表状态，实心圆代表动作。下图是状态值函数的表示。

解释：如上图所示，在某状态下，我们做出的动作取决于我们的策略。在该策略下和状态下，我们要对可能采取的value和action求均值。我们具有一定的概率来决定作出怎样的 action ，而概率是由策略来决定的。也就是说，状态价值函数是所有动作价值函数基于策略π的期望。通俗说就是某状态下所有状态动作价值乘以该动作出现的概率，最后求和，就得到了对应的状态价值。

下图是动作值函数的表示。

解释：如上图所示，我们已经在状态s下采取了a行动，那么该动作值函数等于即时奖励加上转移后新状态值函数均值的折扣。即时奖励是我们在状态s下做出a行动能够立刻得到的奖励。但是环境是未知的，我们自己主动做出这样的action后，环境会以一定的概率（从原状态和action转移到新状态）影响我们行动后的状态。比如，我们要让无人机在空中表演特技，无人机根据当前的风向选择向左飞一点，但它做出这样的行动后，由于风向的不确定性，可能改变原来预期的状态，这是我们不能掌控的。至于折扣因子前面已经说过了，这里不再介绍。

优化值函数

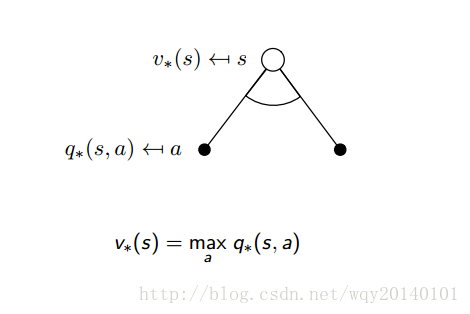
从上图中，我们仍然无法求出最优策略，但至少我们可以得到最优策略下获得的最大奖励是多少。再来看看这个时候的backup diagram：
解释：从上面状态值函数的求法中可以看出，我们不再用期望来表示，而是改用最大值。因为我们现在要找的是最大的状态值函数，也就是说，我们现在关心的是在该状态下，哪一个action能够使当前状态值函数最大，我们就执行哪一个action。

解释：上图是最优动作值函数的求解。完全不同于最优状态值函数，我们没有用到最大值，反而用到了均值。因为我们的agent能做出的，只有action。当action做出后，环境会给我们一个立即奖励，环境同时会以一定概率影响我们下一个状态。这是被动接受，所以我们没有选择最大值，而是继续使用均值来表示我们的最优动作值函数。如果你忘记了什么是 $P_{ss'}^a$，请回顾上一节强化学习简介最后的模型部分。

Optimal Policy（优化策略）

终于到了我们最最最关心的问题了，究竟怎么找到最佳路径呢？首先，想再强调以下什么是 $policy$， $policy$是我们在某个 $state$做出某个 $action$的概率。我们定义，一个 $policy$比另外一个 $policy$更好，在所有 $state$下， $value$都要比另外的 $policy$对应的 $value$值大。以下定义了刚才描述的偏序关系：

注：

• 存在一个最优的 $policy$
• 至少有一个最优的 $policy$。例如，有两个不同的 $action$把 $agent$带到相同的 $state$,这时，这两个 $policy$都可能是最优的。
• 最优policy是由最优动作函数决定的，如下图：
  最优策略就是每次都选择（概率为1）使动作值函数最大的action。

总结

在读第一遍可能晦涩难懂，那就多看几遍。之前本人一直不太喜欢数学公式，但事实上，数学公式以优美的形式，可以更准确地表达。如果没有数学公式，可能整篇文章都是这个，那个，上一个，下一个…让人满头雾水。请正视数学的存在，加油！