前言
明天考图形学了,推一下矩阵,顺便练下 Latex

数学公式警告⚠
模型矩阵
模型矩阵负责将物体进行三个变换:平移,选择和缩放。
此外,我们认为原坐标为 x,变换后则得到 x’ 坐标(接下来的变换都用该形式表示),即:
x → x ′ x \rightarrow x' x→x′
话不多说,开冲!
缩放
缩放矩阵非常简单,各个坐标直接乘以对应的缩放因子即可:
S ( s x , s y , s z ) = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] S(s_x,s_y,s_z)= \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} S(sx,sy,sz)=⎣⎢⎢⎡sx0000sy0000sz00001⎦⎥⎥⎤
旋转
旋转矩阵则分为绕 x,y,z 轴的旋转。以绕 z 轴的旋转为例,我们有如下的极坐标:
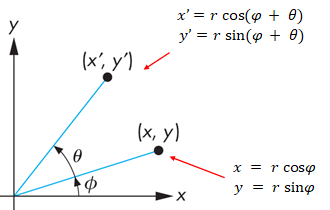
将极坐标展开就是:
x ′ = r c o s ϕ c o s θ − r s i n ϕ s i n θ y ′ = r s i n ϕ c o s θ + r c o s ϕ s i n θ x' = r \ cos\phi \ cos\theta - r \ sin\phi \ sin\theta \\ y' = r \ sin\phi \ cos\theta + r \ cos\phi \ sin\theta x′=r cosϕ cosθ−r sinϕ sinθy′=r sinϕ cosθ+r cosϕ sinθ
将原本 xy 的极坐标:
x = r cos ϕ y = r sin ϕ x = r\cos\phi \\ y = r\sin\phi x=rcosϕy=rsinϕ
带入 x’ 的极坐标展开,那么有
x ′ = x cos θ − y sin θ y ′ = x sin θ + y cos θ x' = x\cos\theta-y\sin\theta \\ y' = x\sin\theta+y\cos\theta \\ x′=xcosθ−ysinθy′=xsinθ+ycosθ
又因为是在 xoy 平面上进行旋转,那么有:
z ′ = z z' = z z′=z
即最终的变换矩阵有:
R z ( θ ) = [ c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] R_z(\theta)= \begin{bmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} Rz(θ)=⎣⎢⎢⎡cosθsinθ00−sinθcosθ0000100001⎦⎥⎥⎤
同理,得到绕 x,y 轴的变换矩阵(原理一样的):
R x ( θ ) = [ 1 0 0 0 0 c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 ] R_x(\theta)= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} Rx(θ)=⎣⎢⎢⎡10000cosθsinθ00−sinθcosθ00001⎦⎥⎥⎤
R y ( θ ) = [ c o s θ 0 − s i n θ 0 0 1 0 0 s i n θ 0 c o s θ 0 0 0 0 1 ] R_y(\theta)= \begin{bmatrix} cos\theta & 0 & -sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ sin\theta & 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} Ry(θ)=⎣⎢⎢⎡cosθ0sinθ00100−sinθ0cosθ00001⎦⎥⎥⎤
平移
平移矩阵也简单,即在原坐标的基础上,加上一个常数即可:
T ( t x , t y , t z ) = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] T(t_x,t_y,t_z)= \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} T(tx,ty,tz)=⎣⎢⎢⎡100001000010txtytz1⎦⎥⎥⎤
视图矩阵
视图矩阵负责将世界坐标系下的坐标转换到相机坐标系,即标架的转换!
相机坐标系基底
首先来确定相机坐标系的基底,即基向量。我们可以通过三个变量,确定相机坐标系的(在世界坐标表示下)基,他们是:
- up: 一般为竖直向上向量 (0, 1, 0)
- eye:相机的世界坐标下的位置
- at:相机的视点(就是看向的点)的位置,也是世界坐标系下
即:
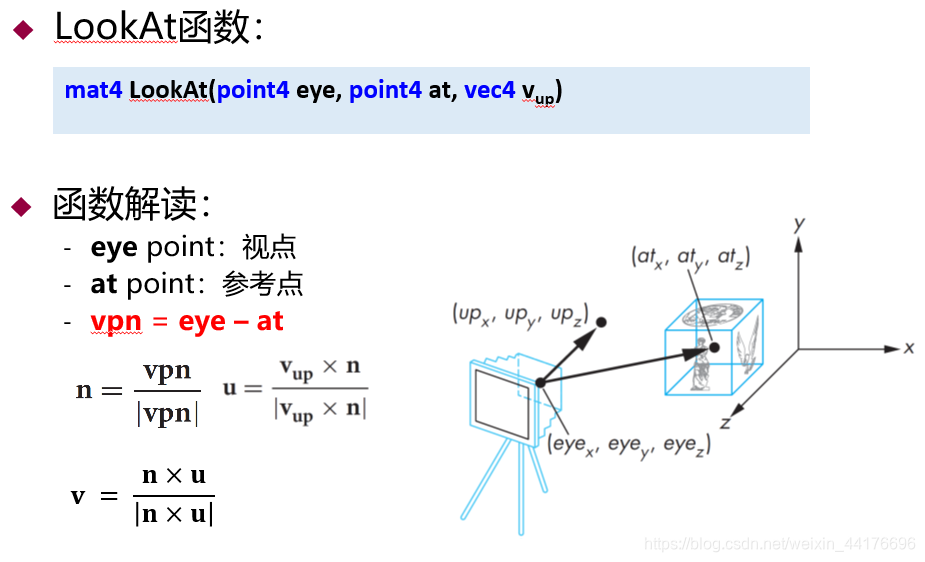
那么我们首先通过:
n ⃗ = e y e − a t \vec{n} = eye-at n=eye−at
得到指向摄像机视平面法向 n
注:
事实上 n 是反的,因为相机看向 z 轴负方向
这也是为何我们要用 eye 减去 at
然后我们再通过 n 和 up 的叉乘,得到指向相机视平面右侧的向量 u:
u ⃗ = u p ⃗ × n ⃗ \vec{u} = \vec{up} \times \vec{n} u=up×n
即:
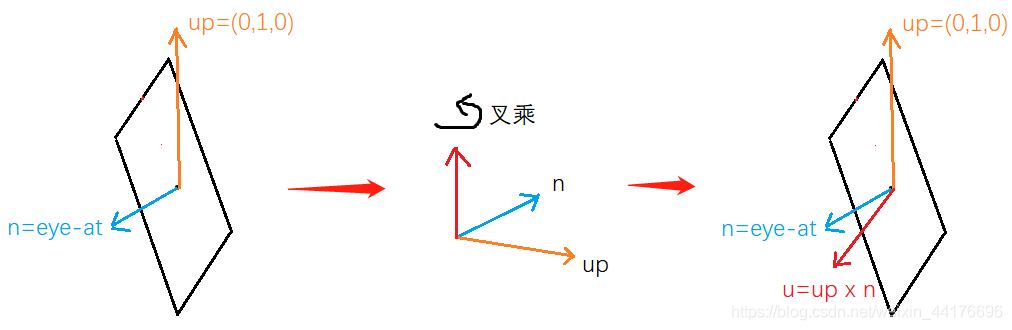
最最后我们通过将 u 和 n 进行叉乘,得到指向相机视平面上方的向量 v:
v ⃗ = n ⃗ × u ⃗ \vec{v} = \vec{n} \times \vec{u} v=n×u
即:
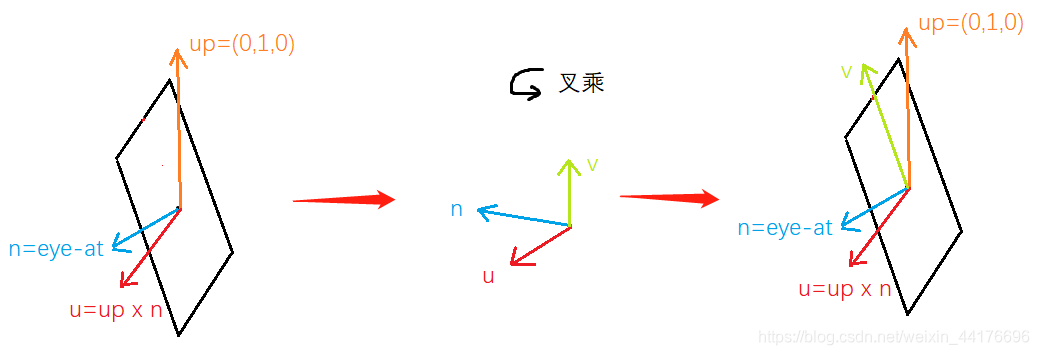
最后我们得到相机坐标系的标架:
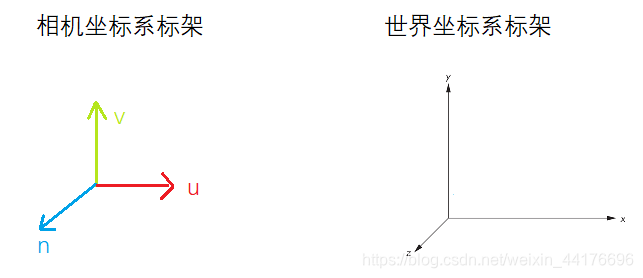
其中有如下的对应关系:
w o r l d P o s → c a m e r a P o s x → u y → v z → n \begin{array}{c} worldPos \rightarrow cameraPos \\ x \rightarrow u \\ y \rightarrow v \\ z \rightarrow n \end{array} worldPos→cameraPosx→uy→vz→n
标架旋转
因为这些标架(u,v,n)是以世界坐标系表示的,那么 u,v,n 就代表相机坐标系坐标轴在世界坐标系坐标轴上的 xyz 轴的 投影。
因为(u,v,n)是单位向量,而不是点,故我们默认相机坐标系和世界坐标原点重合!
我们只需要将世界坐标系旋转一定的角度,就可以表示相机坐标系!
我们通过【相机坐标 * 投影】的方式,就容易将相机坐标转换到世界坐标,即:
w o r l d P o s = M ∗ c a m e r a P o s worldPos = M * cameraPos worldPos=M∗cameraPos
即:
w o r l d P o s = [ u x v x n x 0 u y v y n y 0 u z u z n z 0 0 0 0 1 ] ∗ c a m e r a P o s worldPos = \begin{bmatrix} u_x & v_x & n_x & 0 \\ u_y & v_y & n_y & 0 \\ u_z & u_z & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} * cameraPos worldPos=⎣⎢⎢⎡uxuyuz0vxvyuz0nxnynz00001⎦⎥⎥⎤∗cameraPos
又因为我们需要从世界坐标系转相机坐标系,于是有:
c a m e r a P o s = [ u x v x n x 0 u y v y n y 0 u z u z n z 0 0 0 0 1 ] − 1 ∗ w o r l d P o s cameraPos = \begin{bmatrix} u_x & v_x & n_x & 0 \\ u_y & v_y & n_y & 0 \\ u_z & u_z & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} ^{-1}* worldPos cameraPos=⎣⎢⎢⎡uxuyuz0vxvyuz0nxnynz00001⎦⎥⎥⎤−1∗worldPos
又因为咱们的旋转矩阵是一个正交矩阵,有:
M − 1 = M T M^{-1} = M^{T} M−1=MT
即:
[ u x v x n x 0 u y v y n y 0 u z u z n z 0 0 0 0 1 ] T = [ u x v x n x 0 u y v y n y 0 u z u z n z 0 0 0 0 1 ] − 1 = [ u x u y u z 0 v x v y v z 0 n x n y n z 0 0 0 0 1 ] \begin{bmatrix} u_x & v_x & n_x & 0 \\ u_y & v_y & n_y & 0 \\ u_z & u_z & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} ^{T} =\begin{bmatrix} u_x & v_x & n_x & 0 \\ u_y & v_y & n_y & 0 \\ u_z & u_z & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} ^{-1} =\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} ⎣⎢⎢⎡uxuyuz0vxvyuz0nxnynz00001⎦⎥⎥⎤T=⎣⎢⎢⎡uxuyuz0vxvyuz0nxnynz00001⎦⎥⎥⎤−1=⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎤
于是有:
c a m e r a P o s = [ u x u y u z 0 v x v y v z 0 n x n y n z 0 0 0 0 1 ] ∗ w o r l d P o s cameraPos = \begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}* worldPos cameraPos=⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎤∗worldPos
那么我们通过旋转矩阵即可完成世界坐标到相机坐标的转换:
R = [ u x u y u z 0 v x v y v z 0 n x n y n z 0 0 0 0 1 ] R= \begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} R=⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎤
于是我们完成标架的旋转。
标架平移
刚刚的操作是默认两个坐标系原点重叠,而事与愿违!
我们还要将相机标架移动到 eye 的位置,那么对于世界坐标来说,就是平移 -eye(运动是相对的),于是有平移矩阵:
T = [ 1 0 0 − e y e x 0 1 0 − e y e y 0 0 1 − e y e z 0 0 0 1 ] T= \begin{bmatrix} 1 & 0 & 0 & -eye_x \\ 0 & 1 & 0 & -eye_y \\ 0 & 0 & 1 & -eye_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} T=⎣⎢⎢⎡100001000010−eyex−eyey−eyez1⎦⎥⎥⎤
最终的转换矩阵就是:
v i e w = R ∗ T = [ u x u y u z 0 v x v y v z 0 n x n y n z 0 0 0 0 1 ] ∗ [ 1 0 0 − e y e x 0 1 0 − e y e y 0 0 1 − e y e z 0 0 0 1 ] = [ u x u y u z − u x e y e x − u y e y e y − u z e y e z v x v y v z − v x e y e x − v y e y e y − v z e y e z n x n y n z − n x e y e x − n y e y e y − n z e y e z 0 0 0 1 ] \begin{array}{l} view = R*T=\begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}*\begin{bmatrix} 1 & 0 & 0 & -eye_x \\ 0 & 1 & 0 & -eye_y \\ 0 & 0 & 1 & -eye_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \\ =\begin{bmatrix} u_x & u_y & u_z & -u_x \ eye_x-u_y \ eye_y-u_z \ eye_z \\ v_x & v_y & v_z & -v_x \ eye_x-v_y \ eye_y-v_z \ eye_z \\ n_x & n_y & n_z & -n_x \ eye_x-n_y \ eye_y-n_z \ eye_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{array} view=R∗T=⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎤∗⎣⎢⎢⎡100001000010−eyex−eyey−eyez1⎦⎥⎥⎤=⎣⎢⎢⎡uxvxnx0uyvyny0uzvznz0−ux eyex−uy eyey−uz eyez−vx eyex−vy eyey−vz eyez−nx eyex−ny eyey−nz eyez1⎦⎥⎥⎤
投影矩阵
投影分为正交投影和透视投影。先来看正交:
正交投影
首先将视界体的中心移动到原点,然后再进行缩放,缩放到 ±1 的标准视界体:
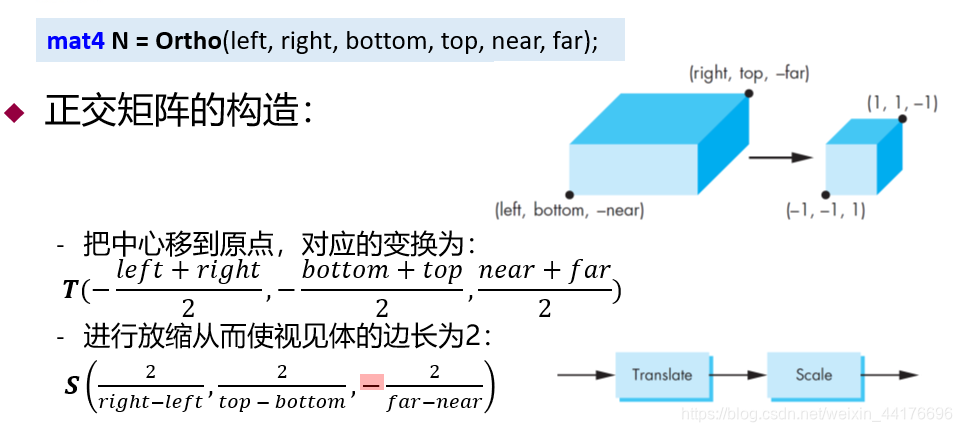
那么有平移矩阵:
T = [ 1 0 0 − l e f t + r i g h t 2 0 1 0 − b o t t o m + t o p 2 0 0 1 n e a r + f a r 2 0 0 0 1 ] T=\begin{bmatrix} 1 & 0 & 0 & -\frac{left + right}{2} \\ 0 & 1 & 0 & -\frac{bottom+ top}{2} \\ 0 & 0 & 1 & \frac{near + far}{2} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} T=⎣⎢⎢⎡100001000010−2left+right−2bottom+top2near+far1⎦⎥⎥⎤
注意负号,因为相机看向 z 负方向。。。
然后是缩放矩阵:
S = [ 2 r i g h t − l e f t 0 0 0 0 2 t o p − b o t t o m 0 0 0 0 − 2 f a r − n e a r 0 0 0 0 1 ] S = \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & -\frac{2}{far-near} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} S=⎣⎢⎢⎡right−left20000top−bottom20000−far−near200001⎦⎥⎥⎤
我们先平移再缩放,于是对应的矩阵为:(先的写右边)
p r o j e c t i o n = S ∗ T = [ 2 r i g h t − l e f t 0 0 0 0 2 t o p − b o t t o m 0 0 0 0 − 2 f a r − n e a r 0 0 0 0 1 ] ∗ [ 1 0 0 − l e f t + r i g h t 2 0 1 0 − b o t t o m + t o p 2 0 0 1 n e a r + f a r 2 0 0 0 1 ] = [ 2 r i g h t − l e f t 0 0 − l e f t + r i g h t r i g h t − l e f t 0 2 t o p − b o t t o m 0 − b o t t o m + t o p t o p − b o t t o m 0 0 − 2 f a r − n e a r − n e a r + f a r f a r − n e a r 0 0 0 1 ] \begin{array}{l} projection=S*T \\ = \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & -\frac{2}{far-near} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}*\begin{bmatrix} 1 & 0 & 0 & -\frac{left + right}{2} \\ 0 & 1 & 0 & -\frac{bottom+ top}{2} \\ 0 & 0 & 1 & \frac{near + far}{2} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \\ = \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & -\frac{left + right}{right-left} \\ 0 & \frac{2}{top-bottom} & 0 & -\frac{bottom+ top}{top-bottom} \\ 0 & 0 & -\frac{2}{far-near} & -\frac{near + far}{far-near} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \end{array} projection=S∗T=⎣⎢⎢⎡right−left20000top−bottom20000−far−near200001⎦⎥⎥⎤∗⎣⎢⎢⎡100001000010−2left+right−2bottom+top2near+far1⎦⎥⎥⎤=⎣⎢⎢⎢⎡right−left20000top−bottom20000−far−near20−right−leftleft+right−top−bottombottom+top−far−nearnear+far1⎦⎥⎥⎥⎤
透视投影
透视讲究近大远小。我们需要根据 z 进行缩放,原理是相似三角形:
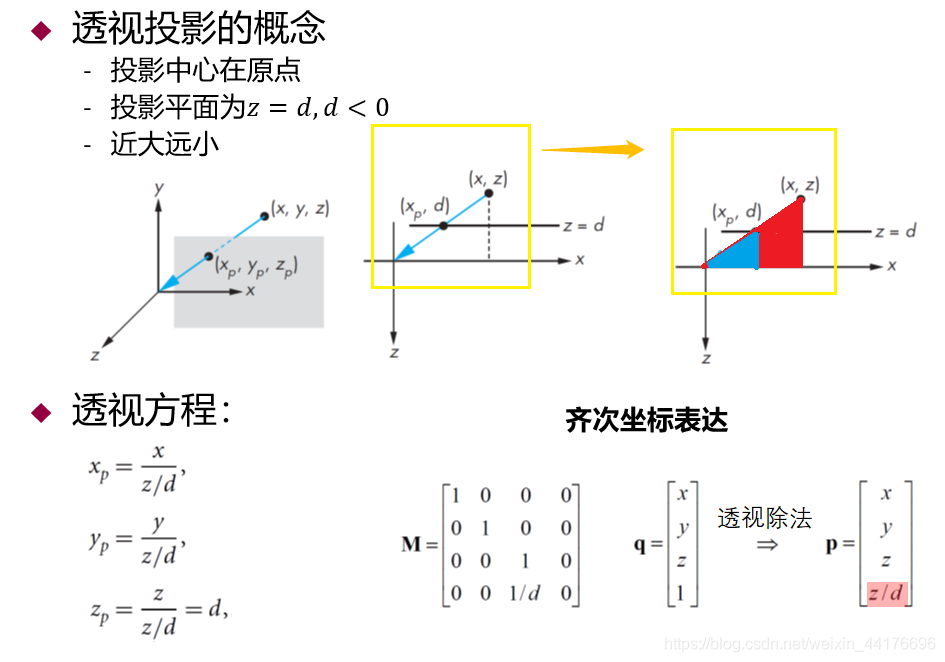
事实上我们也是通过变换,将坐标变换到标准 ±1 的立方体中,我们先保持 xy 不变:
x ′ = x y ′ = y x' = x \\ y' = y x′=xy′=y
此外,标准化的透视除法不应该全部投影到 d 平面上,这意味 z 的坐标不都是 d。需要 z 分量保留深度信息。那么我们应该将 z 坐标变为 :
z ′ = α z + β z' = \alpha z + \beta z′=αz+β
于是我们构造矩阵,使得如下的变换被实现:
x ′ = x y ′ = y z ′ = α z + β w ′ = − z \begin{array}{l} x' = x \\ y' = y \\ z' = \alpha z+ \beta \\ w' = -z \end{array} x′=xy′=yz′=αz+βw′=−z
因为透视除法要求我们除以 w 分量,而 w 分量通常为 -z,这样 透视除法执行之后,我们得到:
x ′ = − x z y ′ = − y z z ′ = − ( α + β z ) \begin{array}{l} x' = -\frac{x}{z} \\ y' = -\frac{y}{z} \\ z' = -(\alpha+ \frac{\beta}{z}) \end{array} x′=−zxy′=−zyz′=−(α+zβ)
此时的变换矩阵是:
[ 1 0 0 0 0 1 0 0 0 0 α β 0 0 − 1 0 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \alpha & \beta \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} ⎣⎢⎢⎡1000010000α−100β0⎦⎥⎥⎤
因为我们不知道 α,β 的值,但是我们希望将 near,far 之间的内容映射到 -1,1 之间,我们带入 z = -1 和 1 的情况, 于是有:
z ′ = − ( α + β n e a r ) = − 1 z ′ = − ( α + β f a r ) = 1 \begin{array}{l} z' = -(\alpha+ \frac{\beta}{near}) = -1 \\ z' = -(\alpha+ \frac{\beta}{far}) = 1 \end{array} z′=−(α+nearβ)=−1z′=−(α+farβ)=1
联立方程组,解得:
α = − f a r + n e a r f a r − n e a r β = − 2 ∗ f a r ∗ n e a r f a r − n e a r \begin{array}{l} \alpha = -\frac{far+near}{far-near} \\ \beta = -\frac{2*far*near}{far-near} \end{array} α=−far−nearfar+nearβ=−far−near2∗far∗near
于是最终的透视投影矩阵有(注意只归一化了 z 轴):
P z = [ 1 0 0 0 0 1 0 0 0 0 α β 0 0 − 1 0 ] = [ 1 0 0 0 0 1 0 0 0 0 − f a r + n e a r f a r − n e a r − 2 ∗ f a r ∗ n e a r f a r − n e a r 0 0 − 1 0 ] P_z= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \alpha & \beta \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} =\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -\frac{far+near}{far-near} & -\frac{2*far*near}{far-near} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} Pz=⎣⎢⎢⎡1000010000α−100β0⎦⎥⎥⎤=⎣⎢⎢⎡1000010000−far−nearfar+near−100−far−near2∗far∗near0⎦⎥⎥⎤
是事实,一种更加规范的透视变换是将 xy 轴也归一化到 ±1 区间,这里偷过来,仅做参考 :
