Unity Shader 图形学,透视投影矩阵,正交投影矩阵的原理及推导,最直观地理解矩阵的意义

前言

我在阅读《unityshader入门精要》时,发现书上并没有给出投影矩阵的推导过程
投影矩阵在图形学有很关键的作用,在游戏开发,虚拟现实和增强现实,机器人学,机器视觉都有涉及到
我想用最直观的方式,解释透视正交投影如何得到的
想要看懂本文,要对缩放旋转平移,3大矩阵要清晰透彻的认识

正交投影

我们先从简单的正交投影开始,想要学习透视矩阵的,建议先学会正交矩阵

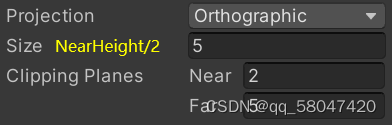
Size:竖直方向上高度的一半,NearHeight/2
Aspect,摄像机横纵比,Aspect=$\frac{NearWidth}{NearHeight}$
根据已知的Size,Near,Far,Apect求出变换矩阵

先将长方体进行缩放,让xyz都在[-1,1],
如下图所示,
对于y轴,对于点2.y=$\frac{NearHeight}{2}$=Size,Size=>1,k₂=$\frac{1}{Size}$
直观的理解就是y轴从Size=>1,y轴缩放大小是$\frac{1}{Size}$
Aspect(简称a)=$\frac{NearWidth}{NearHeight}$,w=ah,x=ay

对于x轴
注意是变换之前a=x/y => x=ay
x’=k₁x
y’=k₂y
x’=y’=1(变换之后的x’,y’坐标都为1)
k₁x=k₂y
k₁=k₂ * $\frac{y}{x}$
a=$\frac{x}{y}$
k1=$\frac{k2}{a}$
k2=$\frac{1}{Size}$
k1=$\frac{1}{Aspect\ast Size}$
w=ah为什么不是k₁=ak₂,而是k₁=k₂/a,这是因为知道的是变换之前的比值,变换之后x’=y’,
假设是横屏,宽度大于高度,即a>1,x>y,想要x’=y’,则x’=kx,k<1,即1/a

对于z轴,观察长方体变换前后的长度,z=Far-Near,z’=2,z轴要翻转,乘以-1,
Far-Near=>2
z’=k₃z,
k₃=$-\frac{2}{Far-Near}$
矩阵:
$$\left[\begin{array}{cccc}\frac{1}{Size}& 0& 0& 0\\ 0& \frac{1}{AspectSize}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& ?\\ 0& 0& 0& 1\end{array}\right]$$
再考虑z轴上的平移就可以求出完整的矩阵了
平移,由2部分组成,如上图所示,在经过缩放后的空间观察,
一部分是,摄像机到裁剪平面的距离,另一部分是正方体长度的一半
摄像机到裁剪平面的距离,由于经过缩放,大小不是Near,而是Near*k₃=$-\frac{2Near}{Far-Near}$
正方体长度的一半,注意z轴翻转了,1,$-\frac{2Near}{Far-Near}$-1=$-\frac{2Near}{Far-Near}$-$\frac{Far-Near}{Far-Near}$
=$\frac{-Near-Far}{Far-Near}$=$-\frac{Far+Near}{Far-Near}$(和书上的写法保持一致)
至此,正交矩阵就推导出来了
$$\left[\begin{array}{cccc}\frac{1}{Size}& 0& 0& 0\\ 0& \frac{1}{AspectSize}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& -\frac{Far+Near}{Far-Near}\\ 0& 0& 0& 1\end{array}\right]$$
如果不理解矩阵为什么要怎么写,可以查查关于缩放旋转平移,3大矩阵的资料

透视投影

1. 基本概念:
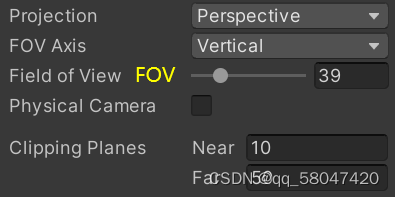
   NearHeight: 近裁剪面的高度
   FarHeight: 远裁剪面的高度
   Near:摄像机离近裁剪面的距离
   Far:摄像机离近裁剪面的距离
   FOV:Field of View,视野范围

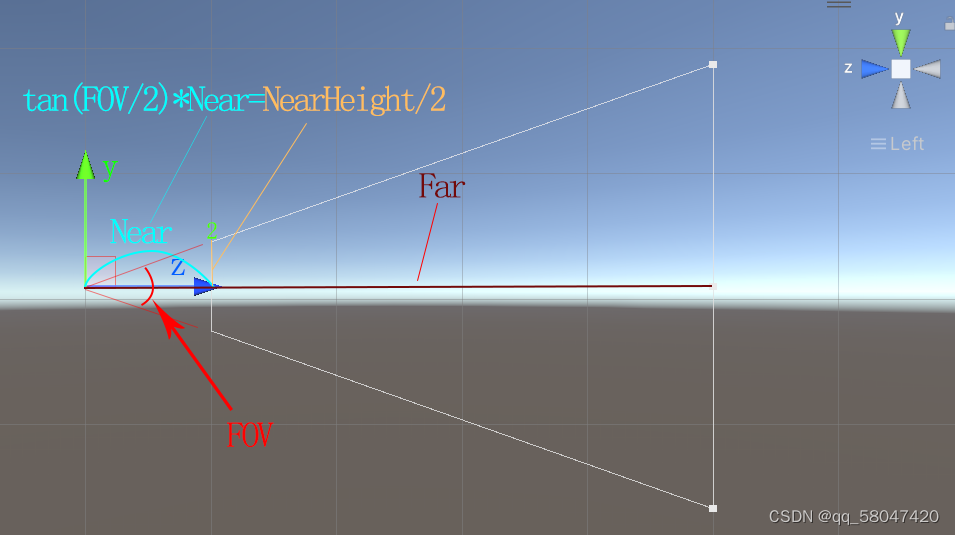
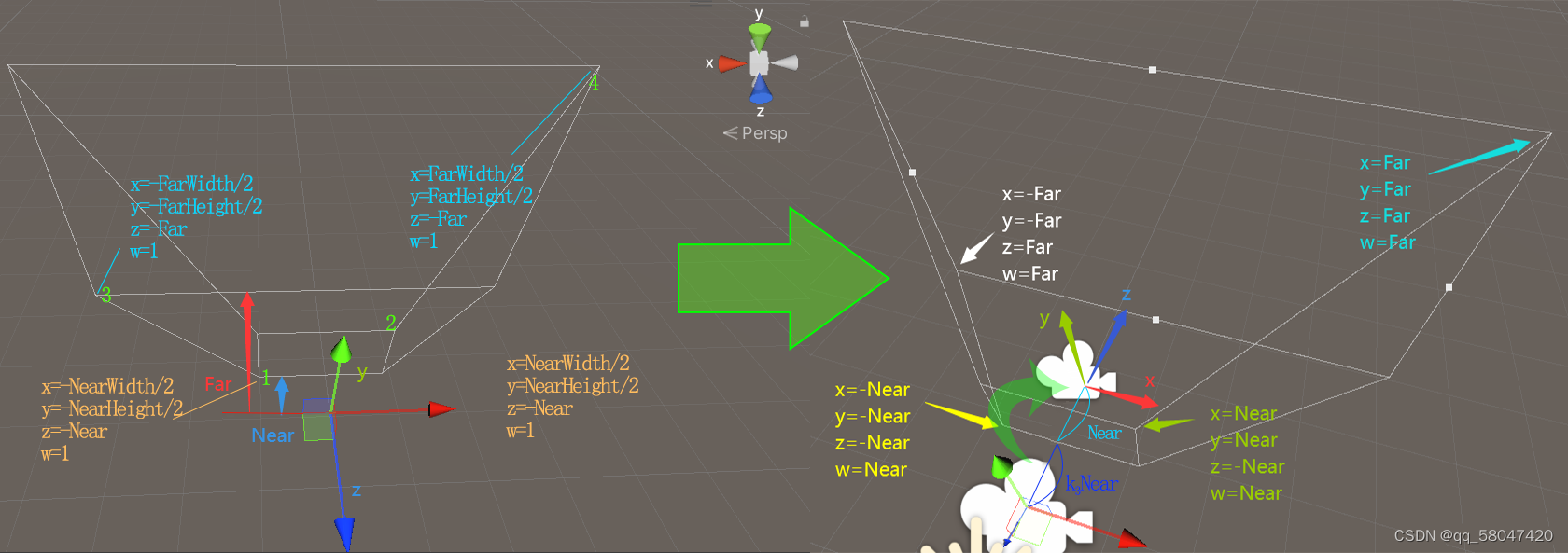
为什么上面的变换不能像正交变换一样,直接转化为[-1,1]标准化的立方体
而是要变换为一个棱台,这是因为矩阵的线性变换,可以将长方体变换为立方体,
无法将一个棱台转换为立方体,棱台转换为立方体需要非线性变换函数,
4×4的变换矩阵,只能对空间进行缩放旋转平移,空间中任意2个原本平行的直线变换后仍然平行,这3大变换显然不能将棱台转换为立方体.因为棱台=>正方体,棱台的两侧的直线不平行=>平行,线性变换无法实现
将w存储变换之前的z,将变换之后的点xyz都除以w,就都变换到[-1,1],此变换是非线性的,缩放值是不固定的,对
不同的平面(平行于xOy的平面),缩放值为平面之前离摄像机的距离
这也是为什么变换后xy有Near,Far
上面的变换可以分为以下几步

• 对视锥体进行缩放,让它的xyzw等于缩放之后的xyzw
• 对视锥体的z方向进行平移
• 翻转z轴

tan$\frac{FOV}{2}$=$\frac{\frac{nearHeight}{2}}{Near}$ ①
tan$\frac{FOV}{2}$等于近裁剪面的高度的一半/Near
Aspect,摄像机横纵比,Aspect=$\frac{NearWidth}{NearHeight}$
先考虑缩放
y轴的缩放,对于下图点2.y来说$\frac{NearHeight}{2}$=>Near
对于y轴,由$\frac{nearHeight}{2}=>Near$,
即将原来的y乘以$\frac{Near}{\frac{NearHeight}{2}}$=>y’
y*$\frac{Near}{\frac{NearHeight}{2}}$=y’
y’=ky,k=$\frac{Near}{\frac{NearHeight}{2}}$②
由①=>cot$\frac{FOV}{2}$=$\frac{Near}{\frac{nearHeight}{2}}$③
由②③得k=cot$\frac{FOV}{2}$
怎么直观理解cot$\frac{FOV}{2}$,
其实就是点2.y变换前后的缩放,
恰好等于Near/近裁剪面的高度的一半,即cot$\frac{FOV}{2}$
因为,NearWidth=Aspect*NearHeight,w=ah
NearHeight=$\frac{NearWidth}{Aspect}$,h=w/a
对于x轴的缩放=y轴的缩放/Aspect
对于x轴,由NearWidth/2=>Near,即将原来的x乘以$\frac{Near}{\frac{NearWidth}{2}}$
w=ah为什么不是k₁=ak₂,而是k₁=k₂/a,这是因为知道的是变换之前的比值,变换之后x’=y’,
假设是横屏,宽度大于高度,即a>1,x>y,想要x’=y’,则x’=kx,k<1,即1/a
对于x轴的缩放有2种方式推导
方法1:
注意是变换之前a=x/y => x=ay
x’=k₁x
y’=k₂y
x’=y’=Near(变换之后的x’,y’坐标都为Near)
k₁x=k₂y
k₁=k₂ * $\frac{y}{x}$
a=$\frac{x}{y}$
k1=$\frac{k2}{a}$
k2=cot$\frac{FOV}{2}$
k1=$\frac{cot\frac{FOV}{2}}{Aspect}$
方法2:
x * $\frac{Near}{\frac{NearWidth}{2}}$=x’,k2=$\frac{Near}{\frac{NearWidth}{2}}$
②=>$\frac{Near}{\frac{h}{2}}$=>$\frac{Near}{\frac{w/a}{2}}$=>$\frac{Near}{\frac{w}{2a}}$
cot$\frac{FOV}{2}$=$\frac{Near}{\frac{nearHeight}{2}}$③
=>cot$\frac{FOV}{2}$=$\frac{Near}{\frac{w}{2a}}$
=>$\frac{cot\frac{FOV}{2}}{a}$=$\frac{Near}{\frac{w}{2}}$
k2=$\frac{Near}{\frac{w}{2}}$=$\frac{cot\frac{FOV}{2}}{a}$
所以,x,y的缩放倍数已经得到
$$\left[\begin{array}{cccc}\frac{cot\frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& cot\frac{FOV}{2}& 0& 0\\ 0& 0& ?& ?\\ 0& 0& ?& 0\end{array}\right]$$
与上面的图片一样,方便查看图片

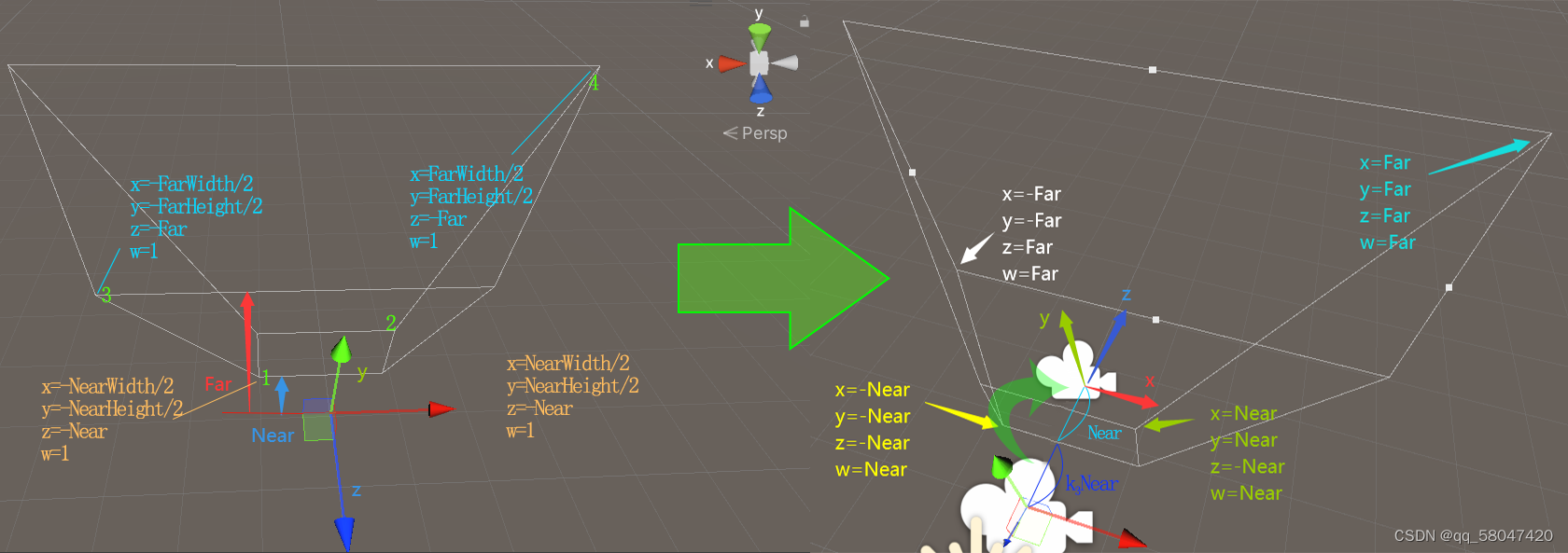
下面讲解怎么得到z轴的缩放
对于视锥体,在z方向,之前视锥体的长度为Far-Near,变换之后的大小为Far+Near,
所以k₃=$\frac{Far+Near}{Far-Near}$,对z轴进行翻转,k₃=-$\frac{Far+Near}{Far-Near}$
下面讲解z轴的平移和z轴的翻转,平移分两部分,在经过缩放后的空间观察,
一部分是变换后的点2的z,即z’₂ =k₃Near,另一部分是Near
z’=k₃z,k₃=$\frac{Far+Near}{Near-Far}$,Near$\frac{Far+Near}{Near-Far}$=$\frac{Near\ast Far+Nea{r}^2}{Near-Far}$
加上变换之后的,-Near(因为z轴的翻转),$\frac{Near\ast Far+Nea{r}^2}{Near-Far}$-Near=
$\frac{Near\ast Far+Nea{r}^2}{Near-Far}$-$\frac{Nea{r}^2-Near\ast Far}{Near-Far}$= $\frac{2\ast Near\ast Far}{Near-Far}$
至此,缩放平移都完成了
要w保存之前的z,设置第4行3列为1即可
透视矩阵就推导出来了
$$\left[\begin{array}{cccc}\frac{cot\frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& cot\frac{FOV}{2}& 0& 0\\ 0& 0& -\frac{Far+Near}{Far-Near}& -\frac{2\ast Near\ast Far}{Far-Near}\\ 0& 0& 1& 0\end{array}\right]$$